The greatest value of the function: $(- 5 sin θ + 12 cos θ)$

Video Solution

Text Solution

Verified by Experts

We know that maximum value of $a sin θ + b cos θ$ is $\sqrt{a^{2} + b^{2}}$ .
In the given expression, $- 5 sin θ + 12 cos θ$ ,
$a = - 5 and b = 12$
$∴$ Maximum value $= \sqrt{- 5^{2} + 13^{2}} = \sqrt{25 + 144} = \sqrt{169} = 13$ .

|

Class 11 MATHS SETS

Similar Questions

If $5 tan θ - 4 = 0$ , then the value of $\frac{5 sin θ - 4 cos θ}{5 sin θ + 4 cos θ}$ is
View Solution
Monotonocity(Greatest and least value OF function)
View Solution
If $3 cos θ = 5 sin θ$ , then $(\frac{5 sin θ - 2 {sec}^{3} θ + 2 cos θ}{5 sin θ + 2 {sec}^{3} θ - 2 cos θ}) = ?$
View Solution
If $5 tan θ = 4$ , then the value of $\frac{5 sin θ - 3 cos θ}{5 sin θ + 3 cos θ}$ is
View Solution
If $tan θ = 1$ then value of $\frac{5 sin θ + 4 cos θ}{5 sin θ - 4 cos θ}$ is
View Solution
If $3 cot θ = 5$ , then $\frac{5 sin θ - 3 cos θ}{5 sin θ + 3 cos θ}$ = ………………
View Solution
Match the greatest value of the function

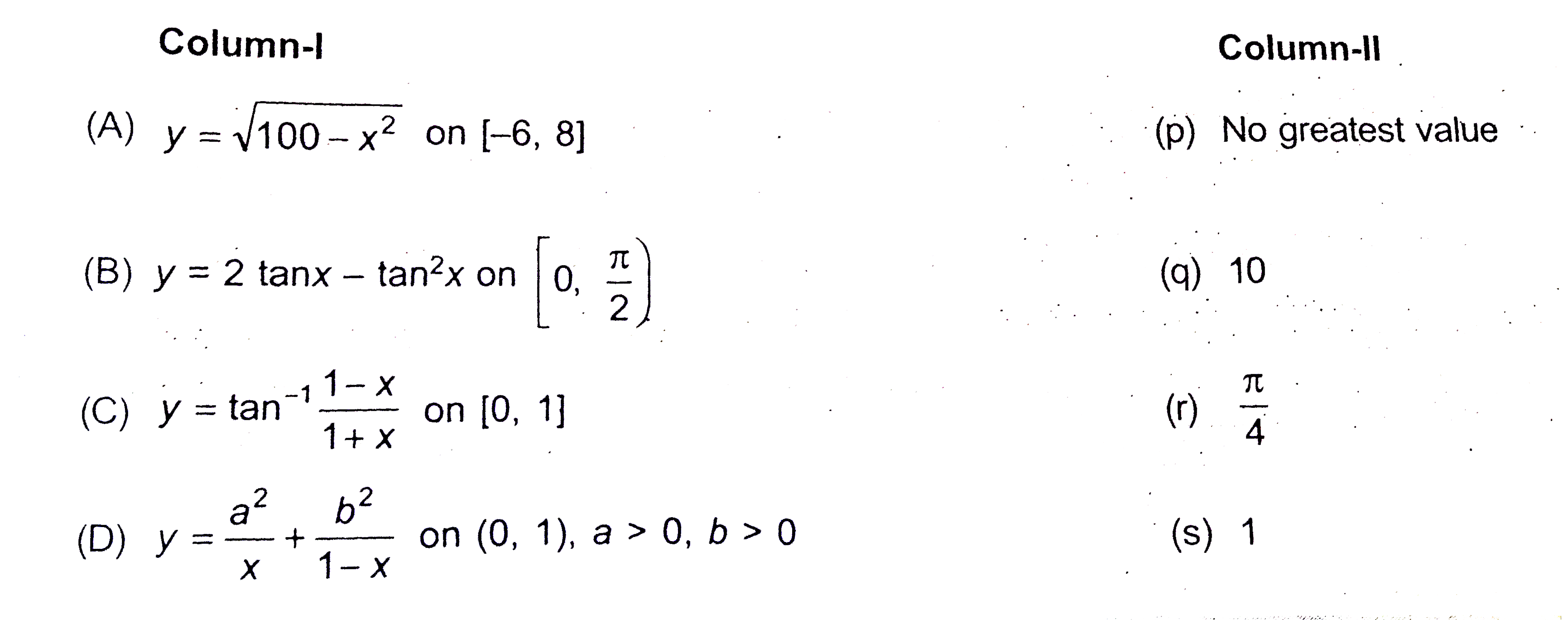
View Solution
If $5 tan θ = 4,$ then $\frac{5 sin θ - 3 cos θ}{5 sin θ + 2 cos θ}$ is equal to
View Solution

Recommended Questions

Home
Ask Doubt
Profile