The area of the triangle bounded by the straight liner ax+by+c=0.(a,b,c≠0) and the coordinate axes is (i)a22|bc|(ii)c22|ba|(iii)b22|ac|(iv)0
Step by step video & image solution for The area of the triangle bounded by the straight liner ax + by + c = 0. (a,b,c!=0) and the coordinate axes is (i) a^2 /( 2|bc| )(ii) c^2/(2|ba| )(iii) b^2/(2|ac| ) (iv) 0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If a2+b2−c2−2ab=0 , then the family of straight lines ax + by + c = 0
Ais concurrent at the pointsB(-1,1)C(1,-1)D(-1,-1)The the area bounded by the curve |x| + |y| = c (c > 0) is 2c2, then the area bounded by |ax + by| + |bx - ay| = c where a2+b2=1 is
A8c2B4c2C2c2Dc2If a+b+c=0 then the family of lines 3ax+by+2c=0 passes through the fixed point
(i) (−2,23)
(ii) (2,33)
(iii) (23,2)
(iv) none of theseA(−2,23)B(2,33)C(23,2)Dnone of these
If the straight line ax+cy=2b, where a,b,c>0, makes a triangle of area 2 sq. units with the coordinate axes, then (a)a,b,c are in GP (b)a, -b; c are in GP (c)a,2b,c are in GP (d) a,−2b,c are in GP
View SolutionIf the straight line ax+cy=2b, where a,b,c>0, makes a triangle of area 2 sq. units with the coordinate axes, then (a) a,b,c are in GP (b) a, -b, c are in GP (c) a,2b,c are in GP (d) a,−2b,c are in GP
View SolutionIf the straight line ax+cy=2b, where a,b,c>0, makes a triangle of area 2 sq. units with the coordinate axes, then (a)a,b,c are in GP (b)a, -b; c are in GP (c)a,2b,c are in GP (d) a,−2b,c are in GP
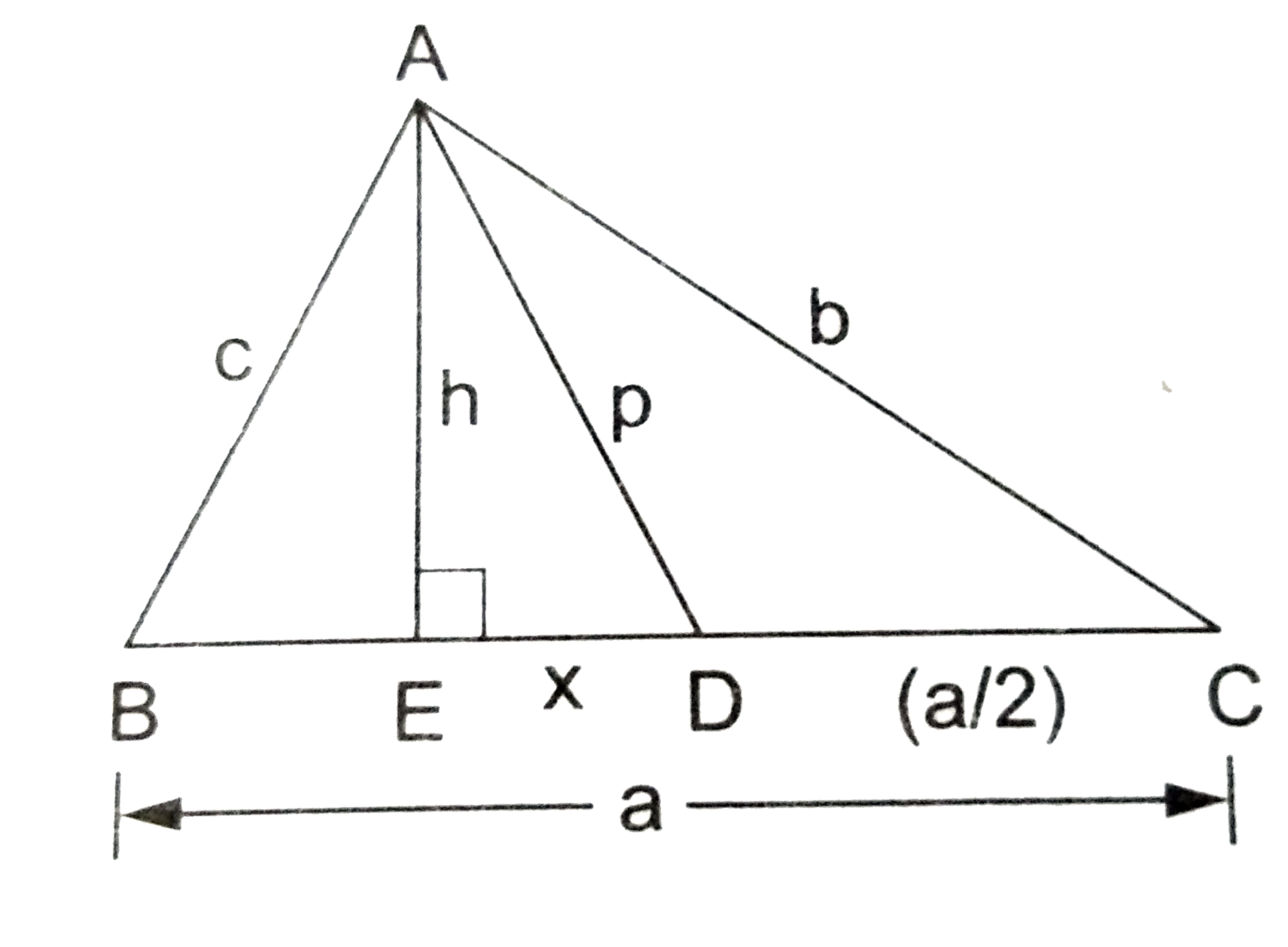
View SolutionIn the given figure, D is the midpoint of side BC and AE⊥BC. If BC=a,AC=b,AB=c,ED=xAD=pandAE=h prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii) (b2+c2)=2p2+12a2
(iv)(b2−c2)=2ax.
View SolutionIf the equation x2+2x+3=0 and ax2+bx+c=0,a,b,c∈R, have a common root, then a : b:c is
View Solution
