A particle A having a charge of C is fixed in a vertical wall. A second particle B of mass 100g and having equal charge is suspended by a silk thread of length 30 cm from the wall. The point of suspension is located 30 cm vertically above the first particle. Find the angle of the thread with the vertical when it stays in equilibrium.
The situation is show in the figure. Let the point of suspension be O, where the thread makes an angle with the vetical. Forces on the particle B are (1) weight mg acting downward. (2) tension, T along the thread, (3) electric force of repulsion F along AB.
At equilibrium sum of all these forces becomes zero.
From the given figure, OA=OB,
Considering the components along BX, we get
or
Now, and AB = 2(OA)
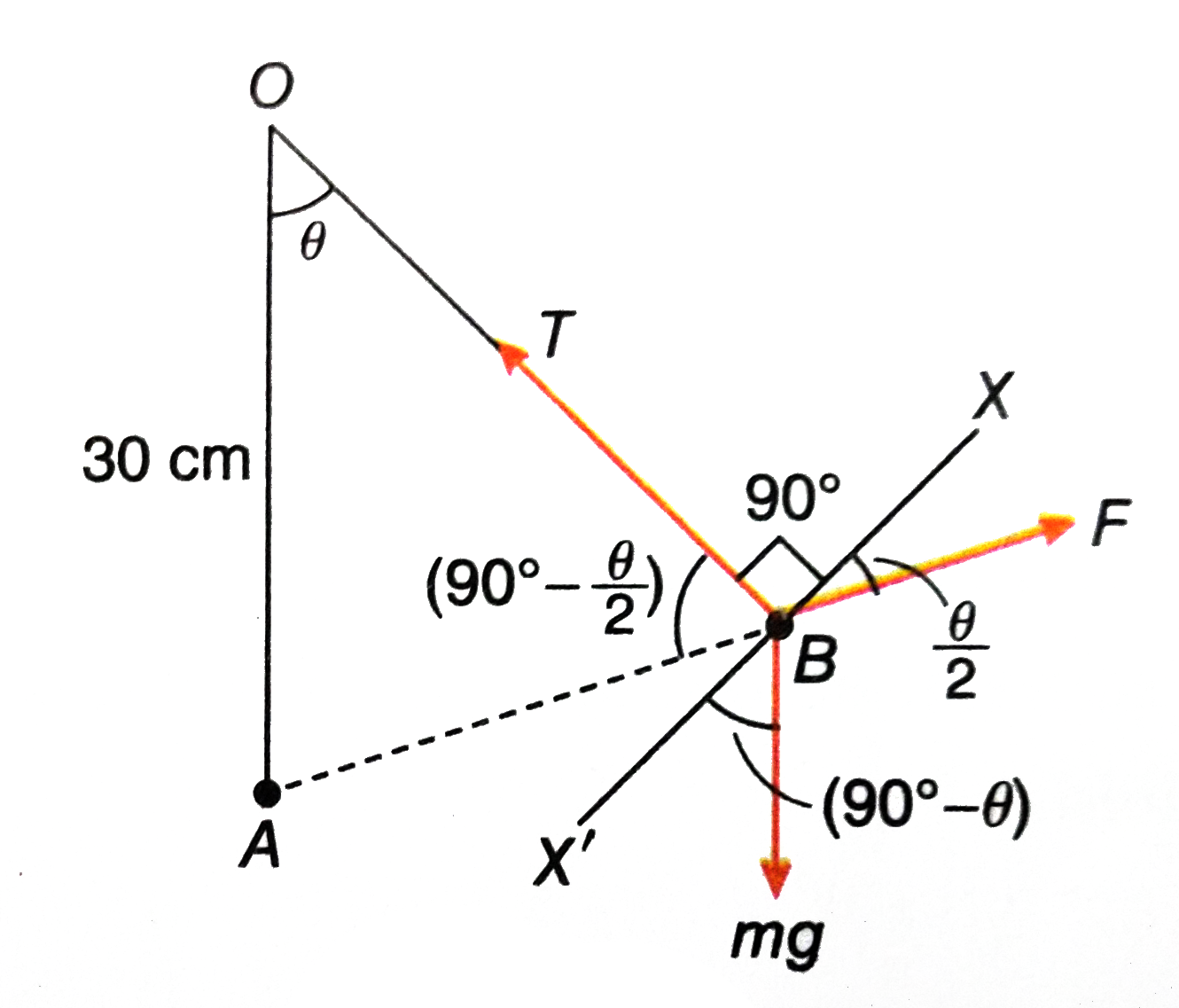
or
=0.0032
or,
Topper's Solved these Questions
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - SECTION RELATION QUESTIONS
50 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - HIGHER ORDER THINKING SKILL QUESTIONS
33 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER
7 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner
13 Videos
Similar Questions
A particle a having a charge of 5.0×10−7C is fixed in. a vertical wall. A second particle B of mass 100 g and. having equal charge is supended by a silk thread. of length 30 cm form the wall. The point of suspension is. 30 cm above the particle A. Find the angle of the thread. with the vertical when it stays in equilibrium.
View SolutionA particle a having a charge of 5.0×10−7C is fixed in. a vertical wall. A second particle B of mass 100 g and. having equal charge is supended by a silk thread. of length 30 cm form the wall. The point of suspension is. 30 cm above the particle A. Find the angle of the thread. with the vertical when it stays in equilibrium.
View Solution
Knowledge Check
A simple pendulum of mass m and charge +q is suspended vertically by a massless thread of length l. At the point of suspension, a point charge +q is also fixed. If the pendulum is displaced slightly from equilibrium position, its time period will be
AT=2π ⎷lg+kq2ml2BT=2πCT=2π√lgDwill be greater then 2π√lg
A particle A having a charge of 2.0×10−6C is held fixed on a horizontal table. A second charged jparticle of mass 80g stays in equilibrium on the table at a distance of 10 cm from the firsst charge. The coefficient of friction between the table and this second jparticle is μ=0.2. find the range within which the charge of this second particle may lie.
View SolutionA particle A having a charge of 2.0×10−6C is held fixed on a horizontal table. A second charged jparticle of mass 80g stays in equilibrium on the table at a distance of 10 cm from the firsst charge. The coefficient of friction between the table and this second jparticle is μ=0.2. find the range within which the charge of this second particle may lie.
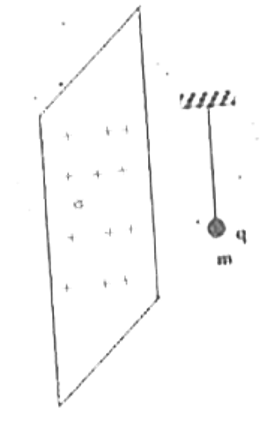
View SolutionA small charged particle of mass m and charge q is suspended by an insulated thread in front of a very large conducting charged sheet of uniform surface density of charge σ. The angle made by the thread with the vertical in equilibrium is
View SolutionTwo identical point charges q of mass m each are suspended through strings of equal length l from a common point of suspension. Find the charge q if angle subtended by the strings with the vertical is θ, when point charges are in a state of equilibrium.
View SolutionTwo small spheres, each of mass 0.1 gm and carrying same charge 10−9C are suspended by threads of equal length from the same point. If the distance between the centres of the sphere is 3 cm, then find out the angle made by the thread with the vertical. (g=10m/s2) & tan^(-1) (1/100) =0.6^(º)
View SolutionTwo small spheres, each of mass 0.1 gm and carrying same charge 10−9C are suspended by threads of equal length from the same point. If the distance between the centres of the sphere is 3 cm, then find out the angle made by the thread with the vertical. (g=10m/s2) & tan−1(1100)=0.6º
View SolutionA water particle of mass 10.0 mg and having a charge of 1.50×10−6C stays suspended in a room. What is the magnitude of electric field in the room ? What is its direction?
View Solution
