A uniform electric field along the x - axis is given as,
$\vec{E} = (200 \hat{i}) N \cdot C^{- 1}$ , for $x > 0$
$= (- 200 \hat{i}) N \cdot C^{- 1},$ for $x < 0$
A cylinder of length 20 cm and radius 5 cm has its centre at the origin and axis along the x - axis is placed in vacuum. find out (i) the electric flux across each of its circular faces, (ii) the flux across its curved surface, (iii) the flux across its centre outer surface and (iv) the net charge enclosed by it.

Text Solution

Verified by Experts

Radius of the cylinder, $r = 5 c m = 0.05 m$
$∴$ Area of each circular face,
$S = π r^{2} = 3.14 \times {(0.05)}^{2} m^{2}$

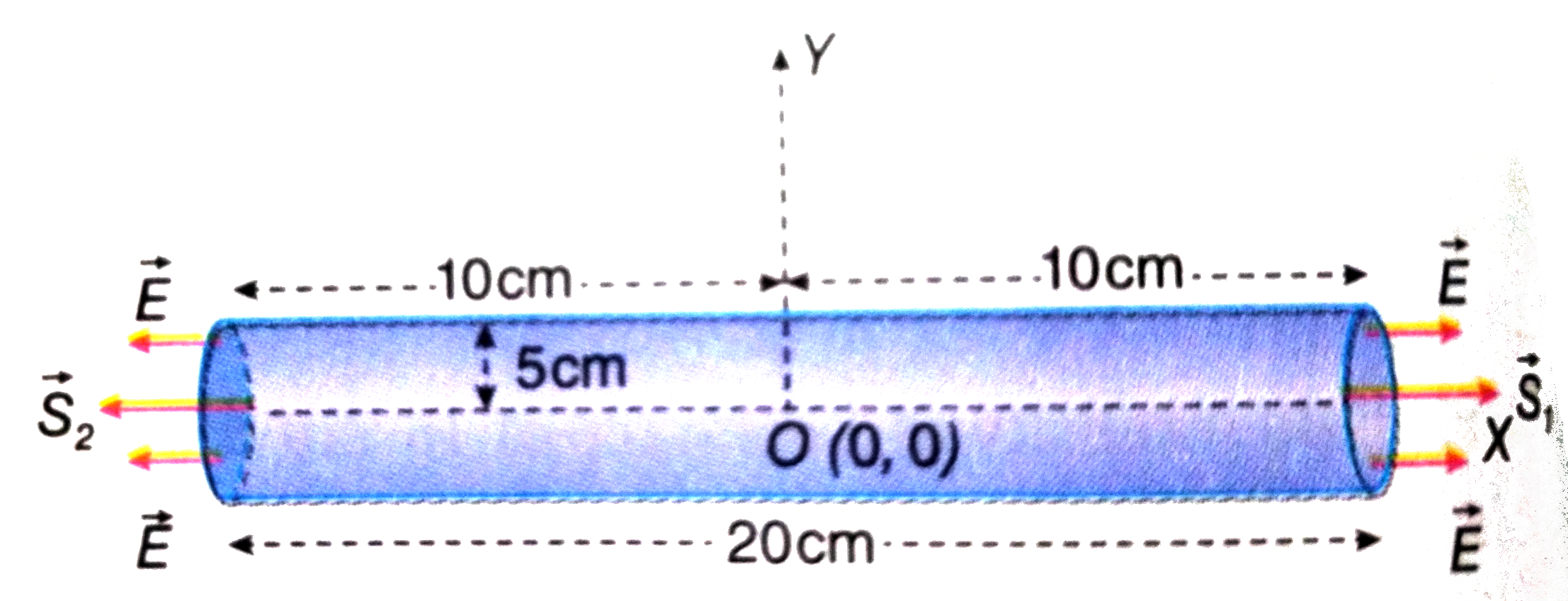
As the length of the cylinder is 20 cm or 0.2 m, the two circular faces are at $x = + 0.1 m and x = - 0.1 m$ .
The area vectors representing the right and the left circular faces are ${\vec{S}}_{1} = \hat{i} (π r^{2}) and {\vec{S}}_{2} = - \hat{i} (π r^{2})$ respectively.
the electric fields at the positions of these circular faces are, ${\vec{E}}_{1} = (200 \hat{i}) N \cdot C^{- 1 and {\vec{E}}_{2} = (- 200 \hat{i}) N \cdot C^{- 1}}$ respectively.
(i) The electric flux across the right circular face,
$ϕ_{1} = {\vec{E}}_{1} \cdot {\vec{S}}_{1} = (200 \hat{i}) \cdot \hat{i} (π r^{2})$
$= 200 \times 3.14 \times {(0.05)}^{2} = 1.57 N \cdot m^{2} \cdot C^{- 1}$
Similarly, for the left circular face,
$ϕ_{2} = {\vec{E}}_{2} \cdot {\vec{S}}_{2} = (- 200 \hat{i}) \cdot (- \hat{i} π r^{2})$
$= 200 \times 3.14 \times {(0.05)}^{2} = 1.57 N \cdot m^{2} C^{- 1}$
$∴ ϕ_{1} = ϕ_{2}$ i.e., equal flux passes across each of the two faces.
(ii) The curved surface is everywhere parallel to the electric field vector.
$∴$ The electric flux linked with the curved surface = 0 $. (i i i) T h e e n t i r e o u t e r s u r f a c e c o n s i s t s o f t h e t w o \circ \underset{̲}{a} r f a c e s and t h e c u r v e d s u r f a c e . s o, t h e f l u x l \in k e d w i t h e n t i r e s u r f a c e, $ therefore phi = phi _ 1 + phi _ 2 + 0 = 1.57 + 1.57 + 0 $$ = 3.14 N * m^ 2 * C ^( - 1 ) $ (i v) F r o m G a u s s' t h e or e m, \neq t f l u x$ phi = ( q ) /( in _ 0 ) $. S o t h e e n c l o s e d c h a r \geq i s, $ q = phi in _ 0 = 3.14 xx 8.854 xx 10 ^( - 12 ) $$ = 2.78 xx 10 ^( -11 ) C

Updated on:21/07/2023

A cylinder of length L and radius b has its axis coincident with x-axis. The electric field in this region is $\to E = 200 ˆ i$ . Find the flux through the left end of the cylinder.
A $0$
B $200 π b^{2}$
C $100 π b^{2}$
D $- 200 π b^{2}$
A cylinder of length L and radius b has its axis coincident with the x-axis. The electric field in the region $\to E = 200 ˆ i$ . Find the flux through (i) the left end of cylinder (ii) the right end of cylinder (iii) the cylinder curved surface, (iv) the closed surface area of the cylinder .
A(i) $- 100 π b^{2} (i i) 100 π b^{2} (i i i) 50 π b^{2} (i v) 50 π b^{2}$
B $(i) - 200 π b^{2} (i i) 200 π b^{2} (i i i) 0 (i v) 0$
C $(i) - 100 π b^{2} (i i) 100 π b^{2} (i i i) 100 π b^{2} (i v) 100 π b^{2}$
D $(i) - 200 π b^{2} (i i) 200 π b^{2} (i i i) 200 π b^{2} (i v) 200 π b^{2}$
The electric field in a region is given by $\to E = 200 ˆ i N / C for x > 0 and - 200 ˆ i N / C for x < 0$ . A closed cylinder of length 2m and cross-section area $10^{2} m^{2}$ is kept in such a way that the axis of cylinder is along X-axis and its centre coincides with origin. The total charge inside the cylinder is (Take $e_{0} = 8.25 \times 10^{- 12} C^{2} m^{2} . N$ )
Azero
B $1.86 \times 10^{- 5} C$
C $1.77 \times 10^{- 11} C$
D $35.4 \times 10^{- 8} C$