At a place , the apparent geomagnetic dip in a vertical place is 40∘ and in another plane perpendicular to it is 30∘ .what is the real dip at the place ?
similar problem : If θ1 is the angle of dip of the magnetic axis of a magnetic needle with horizontal at any vertical plane and θ2 is that in another vertical plane at right former prove that real angle of dip , θ is given by cot2θ=cot2θ1+cot2θ2.Solution in Bengali
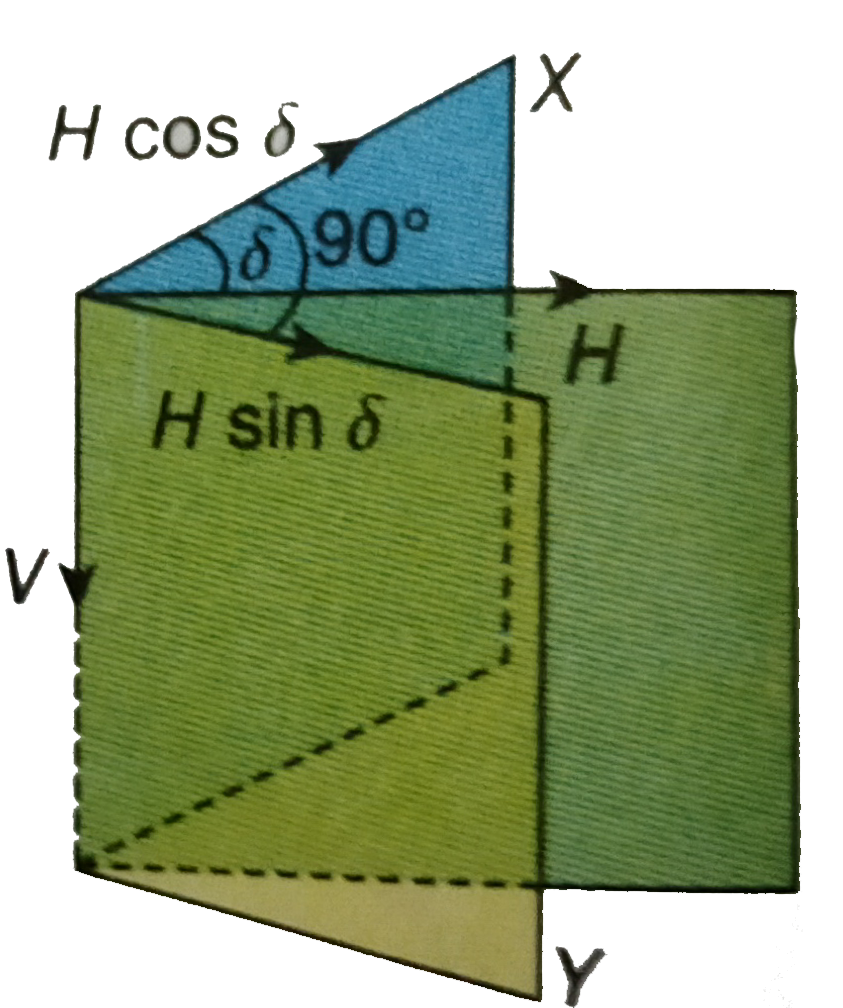
If the horizontal and vertical components of the earth's magnetic field are H and V , respectively and the true dip angle at the place is θ then ,
tanθ=VH ...(1)
In Fig , M is the magnetic meridian and X , Y are two vertical planes inclined at right angle to each other .
The angle between the planes X and M is δ . If apparent dip in the plane X be θ1 then ,
tanθ1=VHcosδ ...(2)
If the apparent dip in the plane Y be θ2 the, tanθ2=VHsinδ ...(3)
From equations (2) and (3) we det ,
cot2θ1+cot2θ2=H2V2(cos2δ+sin2δ)=H2V2
cot2θ [from equation(1) ]
Here , θ1=40∘andθ2=30∘
∴ cot2θ=cot240∘+cot230∘
or, cotθ=√1.42+3=√4.42=2.1
or, θ=cot−1(2.1)=25.46∘
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - Magnetic Properties of Materials EXERCISE - Section Ralated Questions7videos
Magnetic Properties of Materials
- BOOK - CHHAYA PUBLICATIONCHAPTER - Magnetic Properties of Materials EXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS17videos
Magnetic Properties of Materials
- BOOK - CHHAYA PUBLICATIONCHAPTER - LIGHT WAVE AND INTERFERENCE OF LIGHT EXERCISE - CBSE SCANNER15videos
LIGHT WAVE AND INTERFERENCE OF LIGHT
- BOOK - CHHAYA PUBLICATIONCHAPTER - OPTICAL INSTRUMENTSEXERCISE - CBSE SCANNER8videos
OPTICAL INSTRUMENTS
Similar Questions
Define magnetic moment of a bar magnet .
04:03View SolutionIndicate the magnetic axis and magnetic length for a permanent horse - shoe (U - shaped ) magnet .
03:20View SolutionIn Young's double slit experiment derive the condition for (i) constructive interference and (ii) destructive interference at a point on the screen.
01:36View SolutionDefine the magnifying power of a compound microscope when the final image is formed at infinity . Why must both the objective and the eyepiece of a compound microscope has short focal lengths ? Explain.
03:05View SolutionA dip circle is taken to geomagnetic equator. The needle is allowed to move in a vertical plane perpendicular to the magnetic meridian. The needle will stay
05:57View SolutionThe plane of dip circle is set in the geographic meridian and the apparent dip is θ1. It is then set in a vertical plane perpendicular to the geographic meridian. Now, the apparent dip is θ2. The angle of declination θ at that place is
01:36View SolutionThe true value of dip at a place is 30∘ . The vertical plane carrying needle is turned through 30∘ from magnetic meridian . Calculate apparent value of angle of dip .
View SolutionThe true value of dip at a place is 30^(@) . The vertical plane carrying the needle is turned through 45^(@) from the magnetic meridian . Calculate the apparent value of dip .
01:25View SolutionIn a vertical plane p_(1) making angle 30^(@) with magnetic meridian , apparent angle of dip is 60^(@) . The apparent angle of dip in vertical plane p_(2) , which is perpendicular to plane p_(1) is
01:03View SolutionThe true value of dip at a place is 30∘ . The vertical plane carrying needle is turned through 30∘ from magnetic meridian . Calculate apparent value of angle of dip .
03:11View SolutionThe vertical plane dip circle is perpendicular to the magnetic meridian. The dip needle reads
02:17View SolutionA dip circle is taken to geomagnetic equator. The needle is allowed to move in a vertical plane perpendicular to the magnetic meridian. The needle will stay
01:56View SolutionAt a place true dip angle is 60°. The apparent dip when plane of dip circle is at an angle of 30° with the magnetic meridian is
04:34View SolutionA dip circle is taken to geomagnetic equator. The needle is allowed to move in a vertical plane perpendicular to the magnetic meridian. The needle will stay
01:26View SolutionThe plane of dip circle is set in the geographic meridian and the apparent dip is theta_(1) . It is then set in a vertical plane perpendicular to the geographic meridian. Now, the apparent dip is theta_(2) . The angle of declination theta at that place is
03:19View Solution

