An ideal gas follows a process described by from (C is a constant). Then
if
if
if
if
The correct Answer is:B
To solve the problem, we need to analyze the given relationship for an ideal gas undergoing a process defined by the equation PV2=C, where C is a constant. We will derive the relationships between pressure P, volume V, and temperature T of the gas at two states, (P1,V1,T1) and (P2,V2,T2).
1. Understand the given process: The process is defined by the equation PV2=C. This implies that the product of pressure P and the square of volume V remains constant throughout the process.
2. Relate the two states: From the equation, we can write:
P1V21=P2V22=C
This means:
P1V21=P2V22
3. Express pressure in terms of volume: Rearranging the above equation gives us:
P1P2=V22V21
4. Analyze the relationship: If we assume V2>V1, then V2V1>1 implies:
P1P2>1⟹P1>P2
5. Use the ideal gas law: The ideal gas law states:
PV=nRT
From this, we can express pressure P as:
P=nRTV
6. Substitute into the process equation: Substitute P into the process equation:
nRTVV2=C⟹nRTV=C
This can be rearranged to:
TV=CnR
Let C1=CnR, which is a constant.
7. Relate temperatures at the two states: From the above equation, we have:
T1V1=T2V2
Rearranging gives:
T1T2=V2V1
8. Analyze temperature relationship: Since we assumed V2>V1, it follows that:
T1T2>1⟹T1>T2
9. Conclusion: Based on our analysis, if V2>V1, then T1>T2. Therefore, the correct option is that T1 is greater than T2.
Final Answer:
The correct option is B: T1>T2.
P1V21=P2V22=C
This means:
P1V21=P2V22
P1P2=V22V21
P1P2>1⟹P1>P2
PV=nRT
From this, we can express pressure P as:
P=nRTV
nRTVV2=C⟹nRTV=C
This can be rearranged to:
TV=CnR
Let C1=CnR, which is a constant.
T1V1=T2V2
Rearranging gives:
T1T2=V2V1
T1T2>1⟹T1>T2
The correct option is B: T1>T2.
Topper's Solved these Questions
Similar Questions
For an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
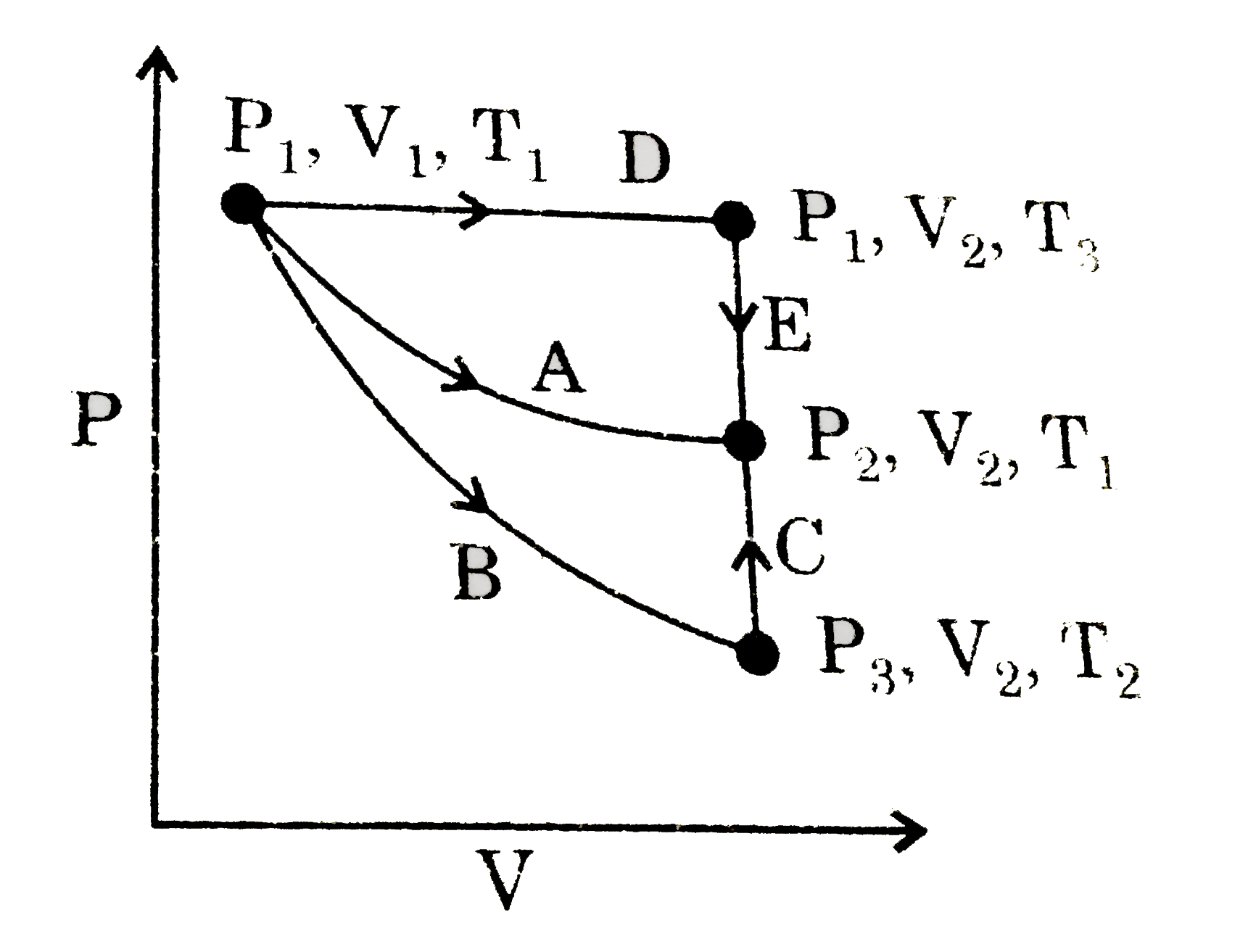
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for (D+E)?View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .

Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for path (A)?View Solution
Knowledge Check
- Question 1 - Select One or More
An ideal gas is expand from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement(s) among the following is (are):
AThe work done by the gas is less when it is expanded reversibly from V1 to V2 under adiabatic conditions as compared to that when expanded reversibly from V1 to V2 under isothermal conditionsBThe change in internal energy of the gas is (i) zero, if it is expanded reversibly with T1=T2, and (ii) positive, if it is expanded reversibly under adiabatic conditions with T1≠T2CIf the expansion is carried out freely, it is simultaneously both isothermal as well as adiabaticDThe work done on the gas is maximum when it is compressed irreversibly from (P2,V2) to (P1,V1) against constant pressure P1 - Question 2 - Select One or More
An ideal gas is expanded from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement (s) among the following is (are)
AThe work done by the gas is less when it is expanded reversibly from V1 to V2 under adiabatic conditions as compared to that when expanded reversibly from V1 to V2 under isothermal conditionsBThe change in internal energy of the gas is (i) zero, if it is expanded reversibly with T1=T2, positive, if it is expanded reversibly under adiabatic conditions with T1≠T2CIf the expansion is carried out freely, it is simultaneously both isothermal as well as adiabaticDThe work done on the gas is maximum when it is compressed irreversibly from (p2,V2) to (p1,V1), against constant pressure p1 - Question 3 - Select One
For an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
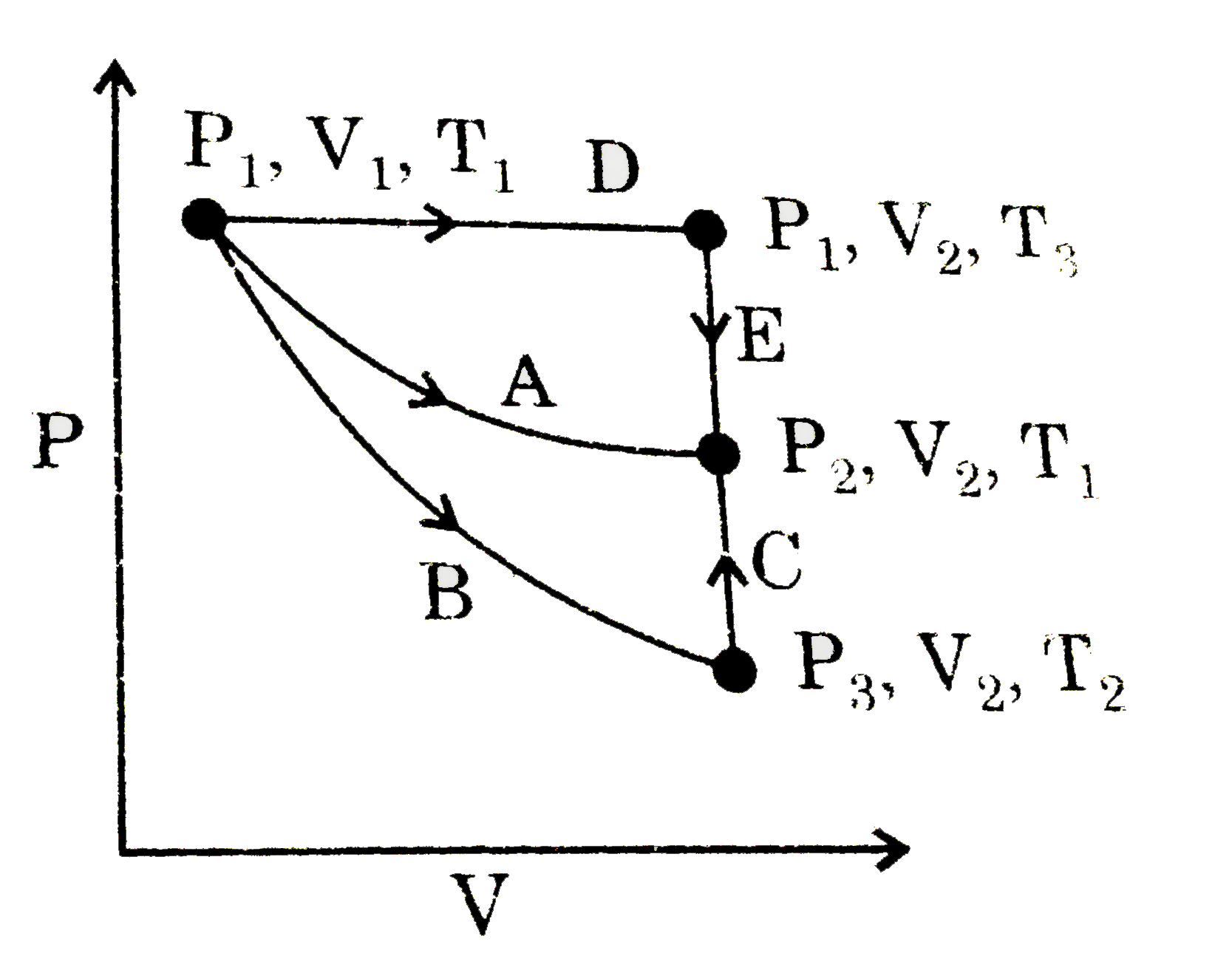
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is qrev for path (A)?AzeroB−nR InV2V1C−nRT1 InV2V1DnRT1 InV2V1
An ideal gas is expand from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement(s) among the following is (are):
View SolutionAn ideal gas is expand from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement(s) among the following is (are):
View SolutionAn ideal gas is expanded from (p1,V1,T1) to (p2,V2,T2) under different conditions. The correct statement(s) among the following is (are).
View SolutionP1V1T1=P2V2T2 is -
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.

Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (B+C)?View Solution

