The space between the plates of a parallel plate air capacitor is filled with an isotropic dielectric medium of which dielectric constant varies in the direction perpendicular to the plates according to the relation given as
Where is the separation, between the plates and is a constant. The area of the plates is . Determine the capacitance of the capacitor.
The correct Answer is:
Topper's Solved these Questions
- CAPACITANCEBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CAPACITANCEEXERCISE - ADVANCE MCQS
26 Videos
- ATOMIC PHYSICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ATOMIC PHYSICSEXERCISE - Unsolved Numerical Problems
39 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
389 Videos
Similar Questions
The gap between the plates of a plane capacitor is filled with an isotropic insulator whose di-electric constant varies in the direction perpendicular to the
plates according to the law K=K1[1+sin(π)dX] where d is the separation, between the plates & K1 is a constant. The area of the plates is S. Determine the capacitance of the capacitor.
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View Solution
Knowledge Check
If the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
AIncreases by a factor 2BIncreases by a factor √2CDecreased by a factor √2DDecreased by a factor 1/2In figure half of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
 A
A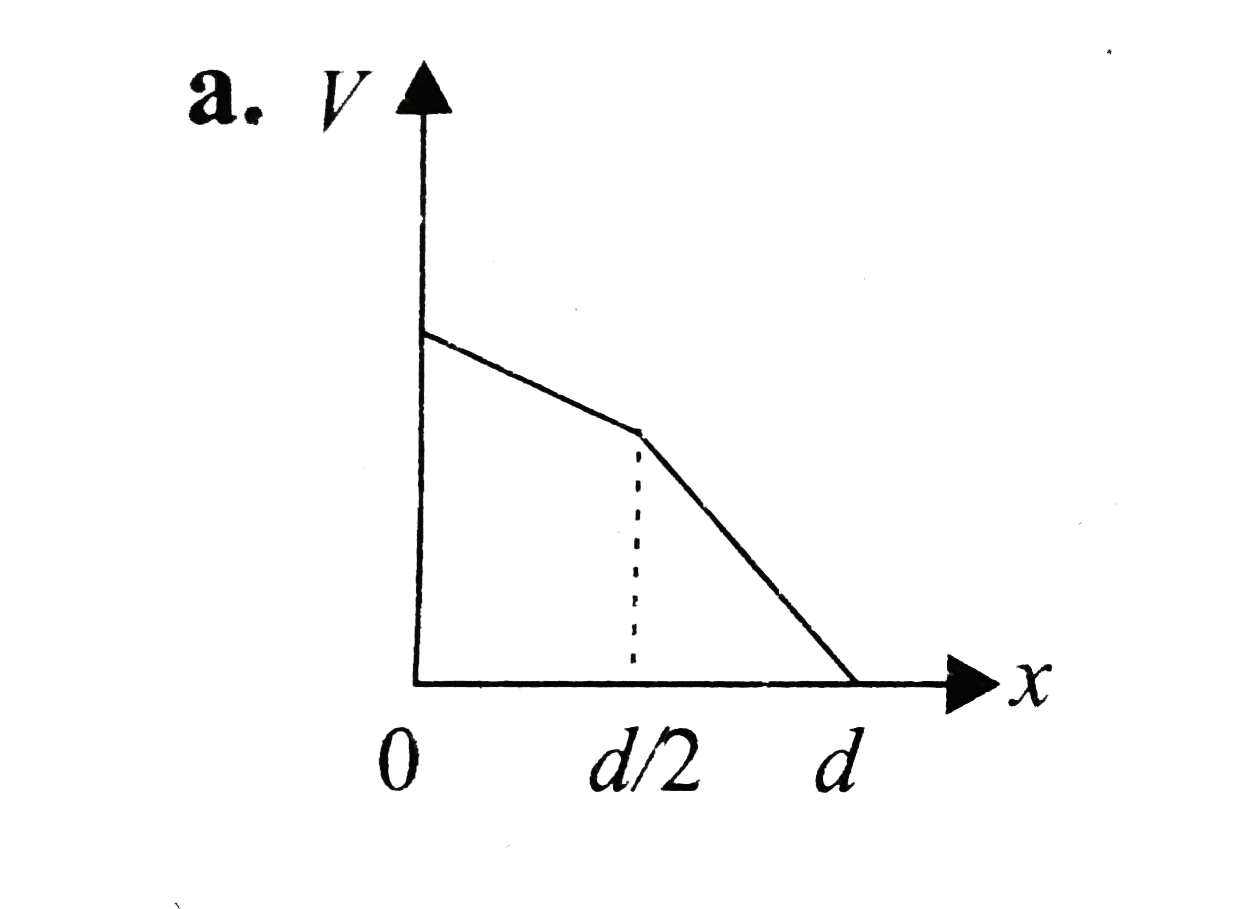 B
B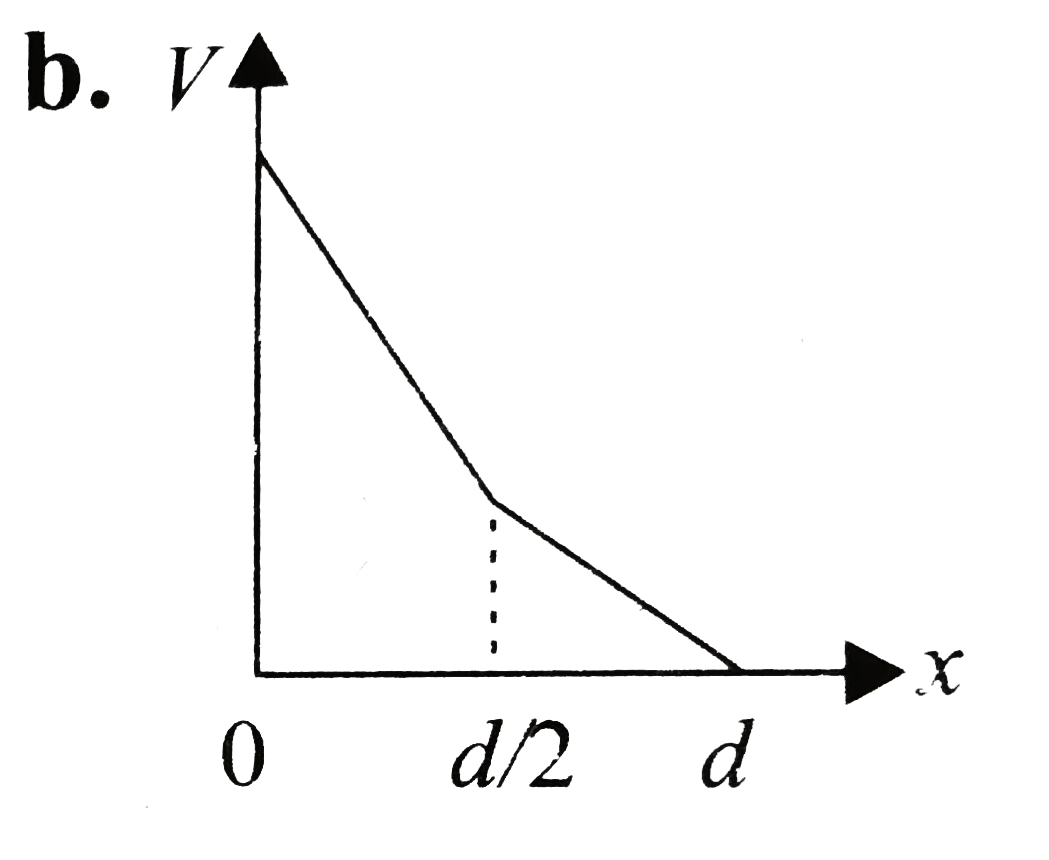 C
C D
D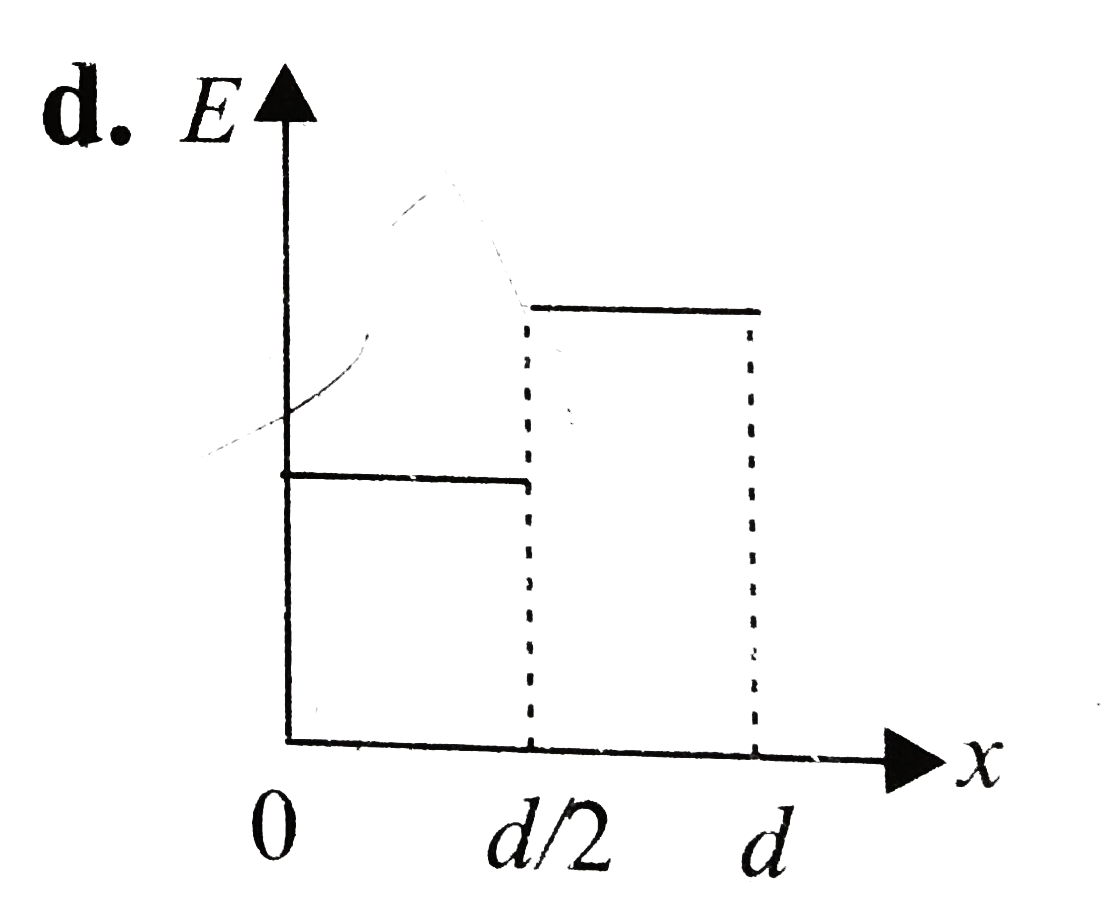
The separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
Aε0Ad−x(1−1K)Bε0Ad+x(1−1K)Cε0Ad+x(1+1K)Dε0Ad−x(1+2K)
Separation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
View SolutionHalf of the space between parallel plate capacitor is filled with a medium of dielectric constant K parallel to the plates . if initially the capacity is C, then the new capacity will be :
View SolutionA parallel plate capacitor has a capacity c. If a medium of dielectric constant K is introduced between plates, the capacity of capacitor becomes
View SolutionA parallel plate capacitor with air between plates (dielectric constant K =2) has a capacitance C. If the air is removed, then capacitance of the capacitor is
View SolutionSeparation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
View Solution
