When a current flows in a conductor, the order of magnitude of drift velocity of electrons through it is :
1010cm/s
104cm/s
10−2cm/s
10−7cm/s
The correct Answer is:C
To determine the order of magnitude of the drift velocity of electrons in a conductor when a current flows through it, we can follow these steps:
Step 1: Understand the formula for drift velocity
The drift velocity vd of electrons in a conductor can be expressed using the formula:
vd=Jn⋅e
where:
- J is the current density,
- n is the number density of charge carriers (electrons),
- e is the charge of an electron.
Step 2: Define the parameters
For a copper wire with a cross-sectional area of A=1mm2=1×10−6m2 carrying a current I=1A:
- The current density J can be calculated as:
J=IA=1A1×10−6m2=1×106A/m2
Step 3: Determine the number density of electrons
For copper, the number density n of conduction electrons is approximately:
n≈8.5×1028electrons/m3
Step 4: Use the charge of an electron
The charge e of an electron is:
e≈1.6×10−19C
Step 5: Substitute values into the drift velocity formula
Now we can substitute the values into the drift velocity formula:
vd=1×106A/m2(8.5×1028electrons/m3)⋅(1.6×10−19C)
Step 6: Calculate the drift velocity
Calculating the denominator:
n⋅e=(8.5×1028)⋅(1.6×10−19)≈1.36×1010C/m3
Now substituting back:
vd=1×1061.36×1010≈7.35×10−5m/s
Step 7: Convert to appropriate units
Converting to centimeters per second:
vd≈7.35×10−5m/s=7.35×10−3cm/s≈10−4m/s
Conclusion
The order of magnitude of the drift velocity of electrons in a conductor carrying a current of 1 A is approximately:
10−4m/s or 10−2cm/s
The drift velocity vd of electrons in a conductor can be expressed using the formula:
vd=Jn⋅e
where:
- J is the current density,
- n is the number density of charge carriers (electrons),
- e is the charge of an electron.
For a copper wire with a cross-sectional area of A=1mm2=1×10−6m2 carrying a current I=1A:
- The current density J can be calculated as:
J=IA=1A1×10−6m2=1×106A/m2
For copper, the number density n of conduction electrons is approximately:
n≈8.5×1028electrons/m3
The charge e of an electron is:
e≈1.6×10−19C
Now we can substitute the values into the drift velocity formula:
vd=1×106A/m2(8.5×1028electrons/m3)⋅(1.6×10−19C)
Calculating the denominator:
n⋅e=(8.5×1028)⋅(1.6×10−19)≈1.36×1010C/m3
Now substituting back:
vd=1×1061.36×1010≈7.35×10−5m/s
Converting to centimeters per second:
vd≈7.35×10−5m/s=7.35×10−3cm/s≈10−4m/s
The order of magnitude of the drift velocity of electrons in a conductor carrying a current of 1 A is approximately:
10−4m/s or 10−2cm/s
Topper's Solved these Questions
Similar Questions
(a) Deduce the relation between current I flowing through a conductor and drift velocity →vd of the electrons.
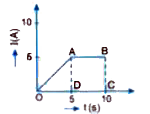
(b) Figure shows a plot of current I flowing through the cross section of a wire versus the time t. Use the plot to find the charge flowing in 10 s through the wire.
View SolutionCalculate the current passing through a conductor (made up of Cu) if 1 mole of electrons flows through it in 1 hour.
View Solution
Knowledge Check
When current flows through a conductor, then the order of drift velocity of electrons will be
A1010m/secB10−2cm/secC104cm/secD10−1cm/secWhen a current flows through a conductor its temperature
AMay increase or decreaseBRemains sameCDecreasesDIncreasesWhen current passes through a conductor,
Ait creates an electric firld around it, directed towards the conductorBit creates an electric field, directed away from the conductorCnone of the aboveDAll of these
When no current is passed through a conductor,
View SolutionDefine relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons ? Use this relation to deduce the expression for the electrical resistivity of the material.
View SolutionWhen the current i is flowing through a conductor, the drift velocity is v . If 2i current is flowed through the same metal but having double the area of cross-section, then the drift velocity will be
View SolutionA current i is flowing through the wire of diameter (d) having drift velocity of electrons vd in it. What will be new drift velocity when diameter of wire is made d/4?
View SolutionIf A is the area of cross section of conductor, vd is the drift velocity of electrons and n is the number of electrons per unit volume, then current density through conductor is
View Solution