The switch is closed at . the capacitor is uncharged but has a charge at . If , , . Calculate i () in the circuit.
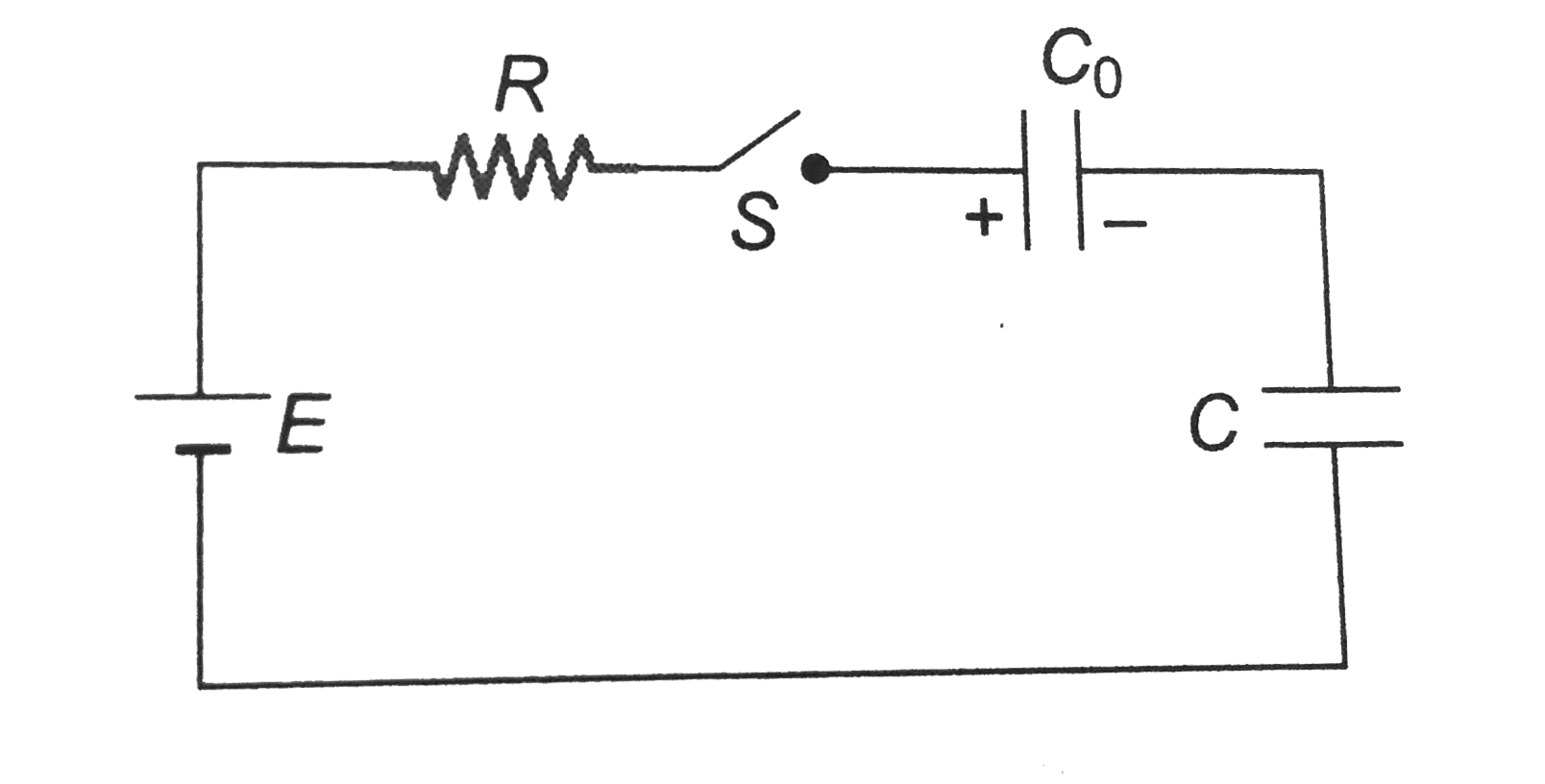
Step by step video & image solution for The switch S is closed at t=0 . the capacitor C is uncharged but C_0 has a charge Q_0=2muC at t=0. If =100Ommega , C=2muF , C_0=2muF,E=4V. Calculate i (t) in the circuit. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
_PHY_E06_157_Q01.png)
Knowledge Check
- Question 1 - Select One or More
In the circuit shown key is closed at t=0 with capacitor initially uncharged.
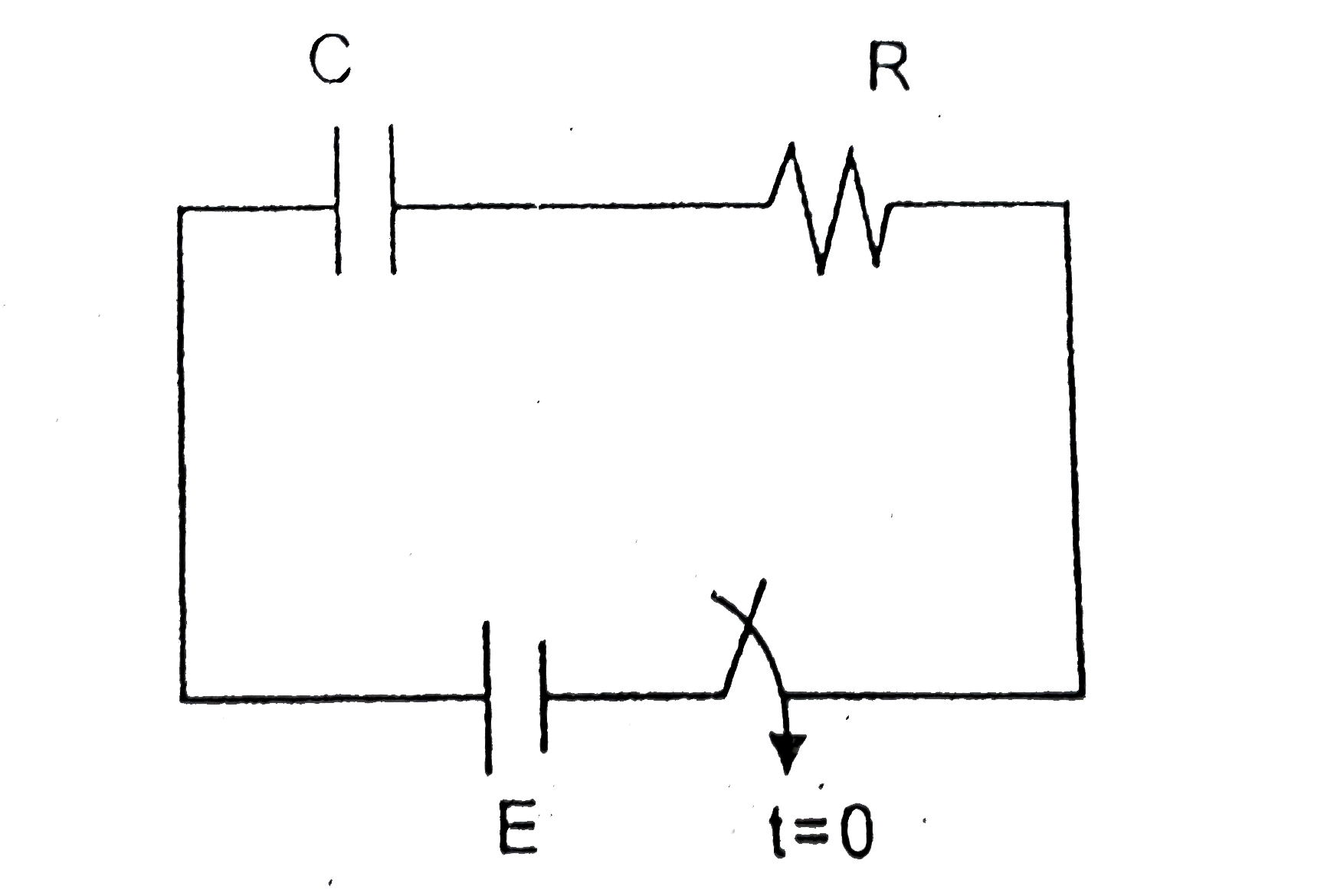ARate of increase of capacitors energy, just after the switch is closed is E2RBMaximum power supplied by the cell is E2RCAt t=RCIn2, capacitor is charged up to half of the energy stored by it in steady stateDAt t=RCIn2, potential difference across capacitor is same that across resistor. - Question 2 - Select One
In the circuit shown, the switch 'S' is closed at t=0. Then capacitor is initially uncharged. Then the current through the resistor R=8Ω at t=0.4×10−3sec is (Take e−2=0.135 )
A0.18AB0.27AC0.54AD0.72A - Question 3 - Select One
In the given circuit switch is closed at t=0. The charge flown in time t=Tc (where Tc is time constant).
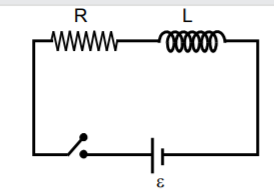AεLR2eBεLR2C(εL)(1−1e)RDεLR
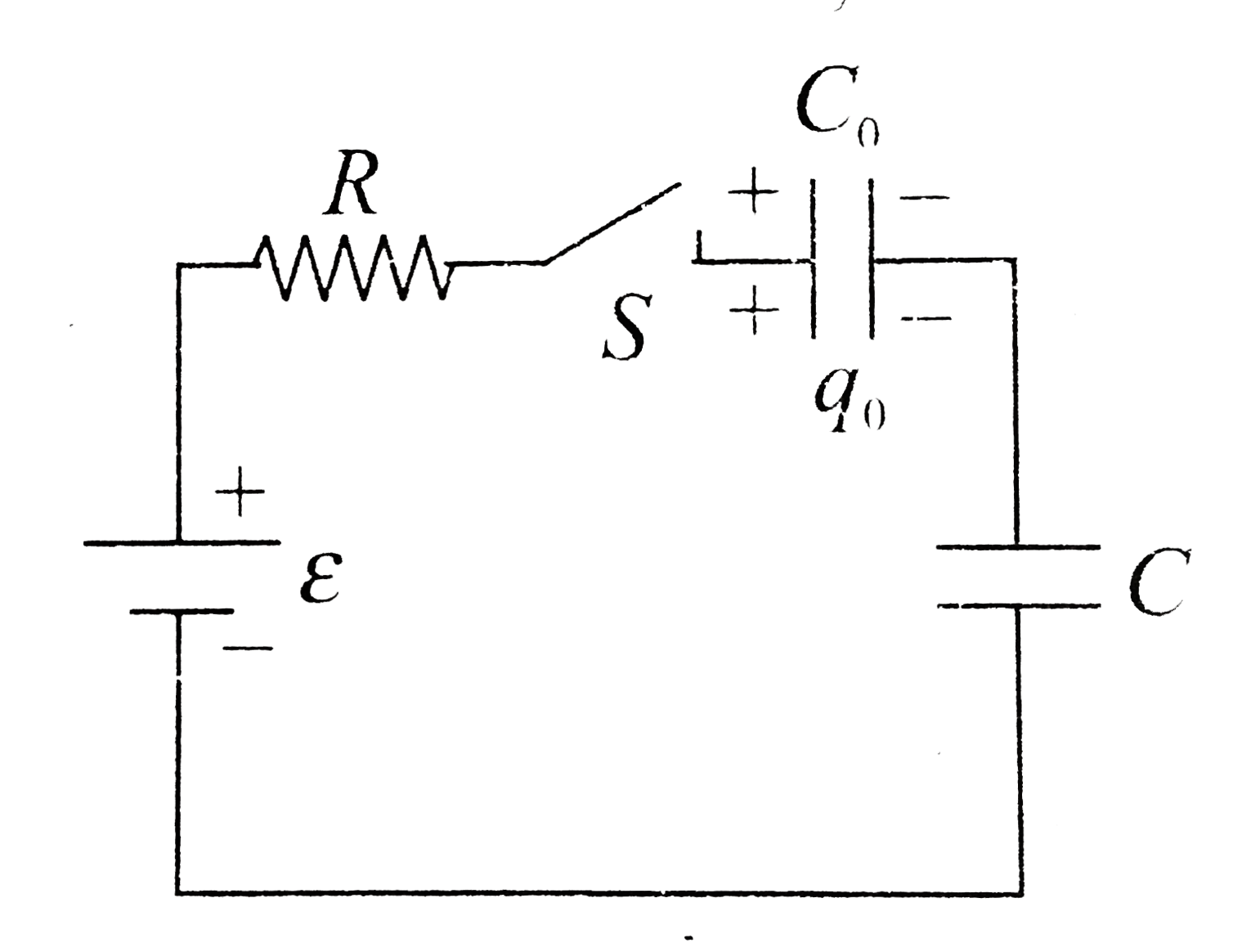
For the arrangement shown in the figure, the switch is closed at t=0. C2 is initially uncharged while C1 has a charge of 2μC
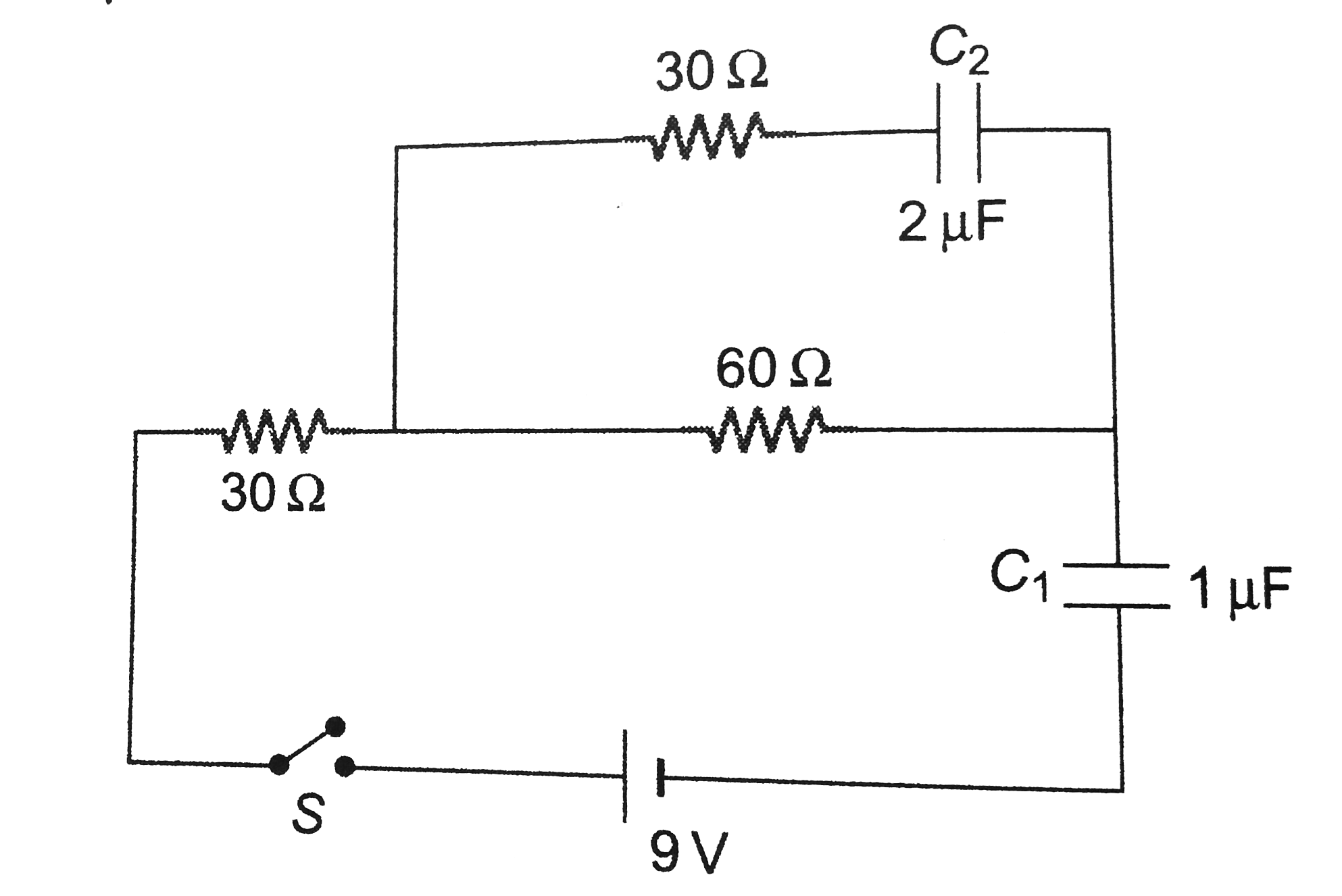
(a) Find the current comingn out of the battery just after the switch is closed.
(b) Find the charge on the capacitors in the steady state condition.View SolutionIn the circuit shown. Initially the capacitor is uncharged. The switch S is closed at time t=0. Then
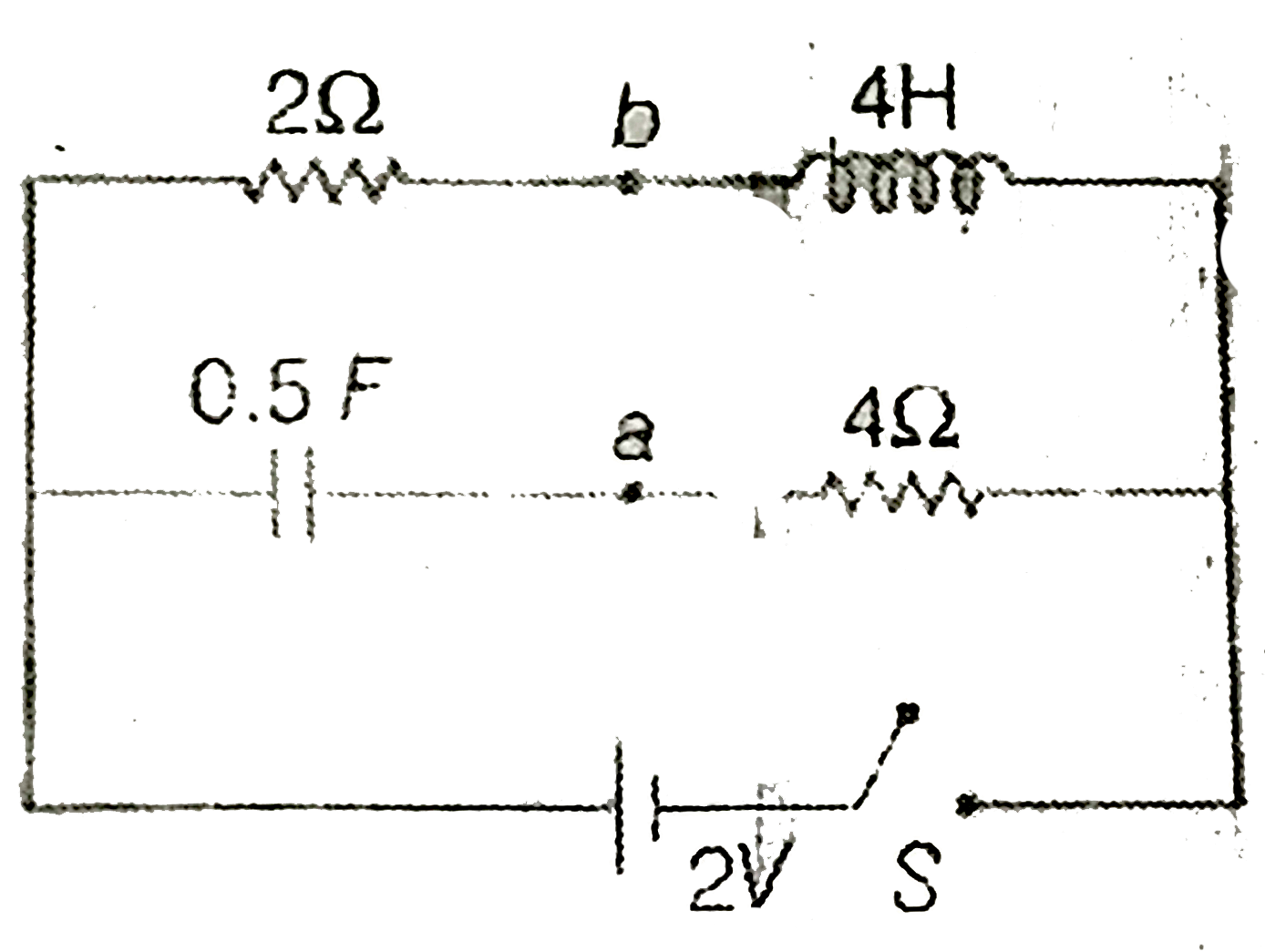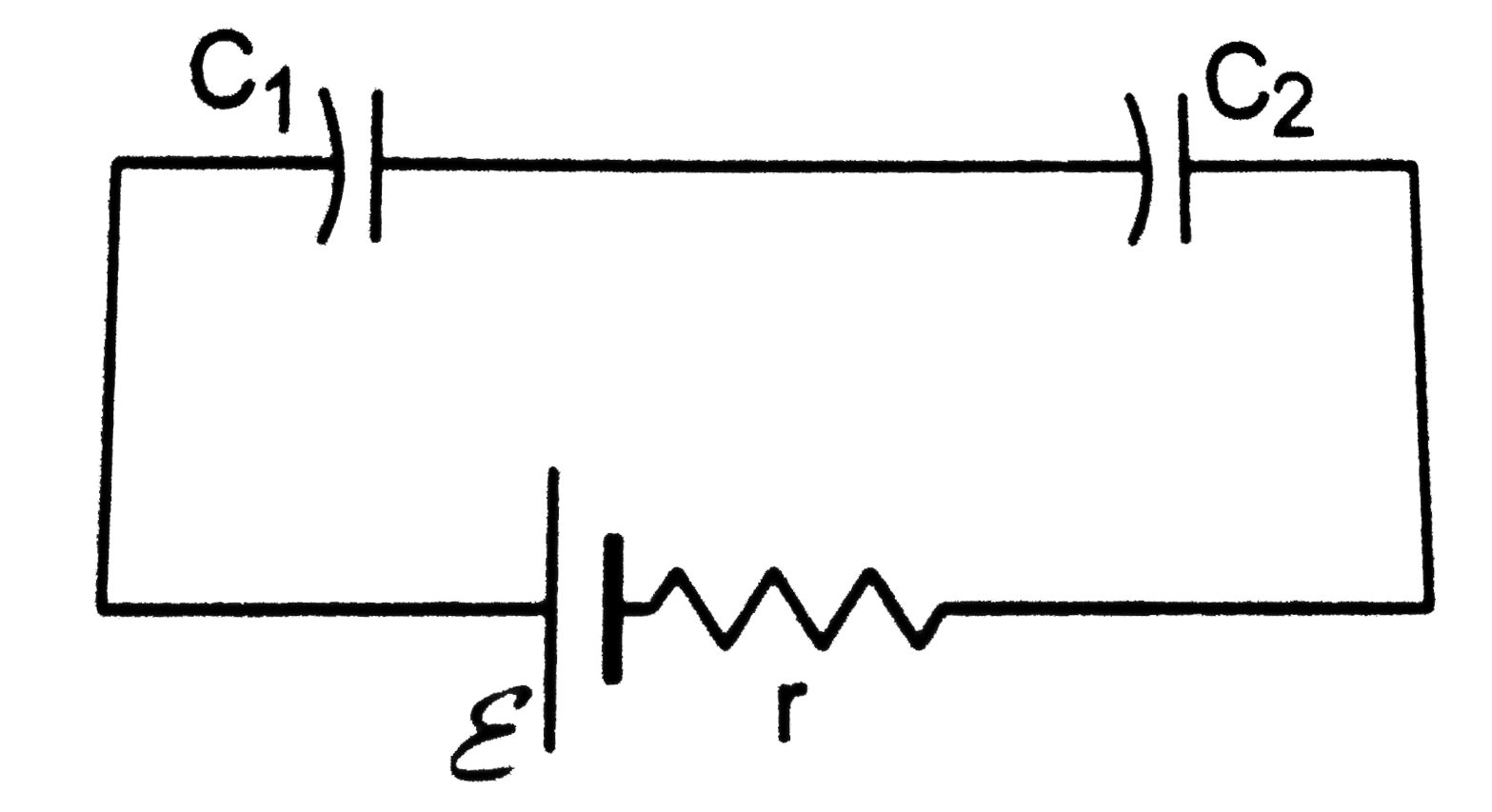
View SolutionConsider the situation shown in figure.The switch is closed at t=0when the capacitor C1as a function of time t.
View SolutionThe switch S of the circuit is closed at t = 0. Find the current (in Amp.) through the capacitor when the switch S is closed at t = 0
View SolutionConsider a simple RC circuit as shown in figure 1.
Process 1 : In the circuit the switch S is closed at t=0 and the capacitor if fully charged to voltage V0 (i.e., charging continues for time T>>RC). In the process some dissipation (ED) occurs across the resistance R. The amount of energy finally stored in the fully charged capacitor is Ec.
Process 2 : In a different process the voltage is first set to V03 and maintained for a charging time T>>RC. Then the voltage is raised to 2C03 without discharging the capacitor and again maintained for a time T>>RC. The process is repeated one more time by raising the voltage to V0 and the capacitor is charged to the same final voltage V0 as in Process 1.
These two processes are depicted in figure 2.
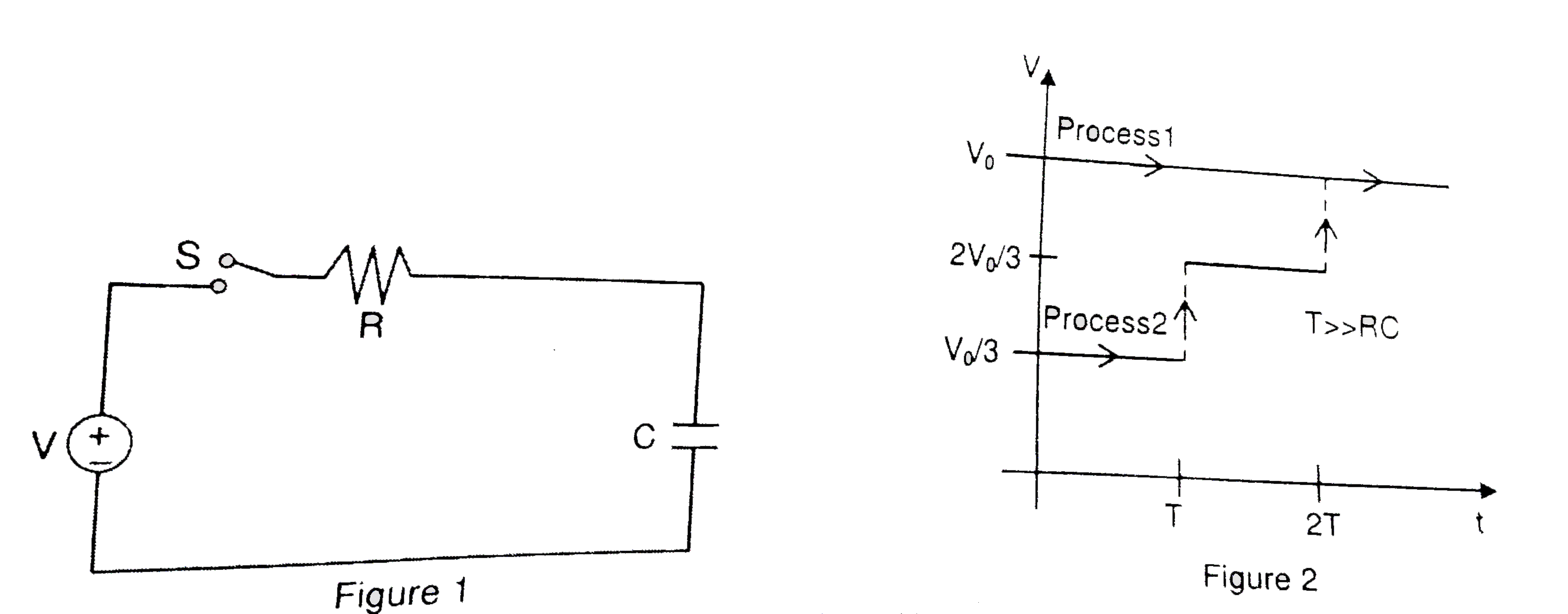
In process 2, total energy dissipated across the resistance ED is :View Solution