Two short electric dipoles having dipole moment p1 and p2 are placed co-axially and uni-directionally, at a distance r apart. Calculate nature and magnitude of force between them :
The correct Answer is:[Attraction, 14πε06p1p2r4]
To solve the problem of finding the nature and magnitude of the force between two short electric dipoles placed coaxially and unidirectionally at a distance r apart, we can follow these steps:
1. Understanding the Configuration:
- We have two dipoles, p1 and p2, placed along the same axis (coaxially) and pointing in the same direction (unidirectionally).
- The distance between the two dipoles is r.
2. Potential Energy of the Dipoles:
- The potential energy U between two dipoles can be expressed as:
U=−14πϵ0⋅2p1⋅p2r3
- Since both dipoles are aligned in the same direction, the angle θ between p and the electric field E is 0∘, and thus cos(0∘)=1.
3. Electric Field Due to a Dipole:
- The electric field E at a distance r due to dipole p2 acting on dipole p1 is given by:
E=14πϵ0⋅2p2r3
4. Substituting Electric Field into Potential Energy:
- Substitute the expression for E into the potential energy formula:
U=−p1⋅E=−p1⋅(14πϵ0⋅2p2r3)
- Thus, we have:
U=−14πϵ0⋅2p1⋅p2r3
5. Calculating the Force:
- The force F between the dipoles can be found by taking the derivative of the potential energy with respect to the distance r:
F=−dUdr
- Differentiating U:
F=−ddr(−14πϵ0⋅2p1⋅p2r3)
- This results in:
F=6p1⋅p24πϵ0r4
6. Nature of the Force:
- The force is positive, indicating that the force is attractive since the potential energy is negative. Therefore, the nature of the force between the dipoles is attractive.
Final Result:
- The magnitude of the force between the two dipoles is:
F=6p1⋅p24πϵ0r4
- The nature of the force is attractive.
- We have two dipoles, p1 and p2, placed along the same axis (coaxially) and pointing in the same direction (unidirectionally).
- The distance between the two dipoles is r.
- The potential energy U between two dipoles can be expressed as:
U=−14πϵ0⋅2p1⋅p2r3
- Since both dipoles are aligned in the same direction, the angle θ between p and the electric field E is 0∘, and thus cos(0∘)=1.
- The electric field E at a distance r due to dipole p2 acting on dipole p1 is given by:
E=14πϵ0⋅2p2r3
- Substitute the expression for E into the potential energy formula:
U=−p1⋅E=−p1⋅(14πϵ0⋅2p2r3)
- Thus, we have:
U=−14πϵ0⋅2p1⋅p2r3
- The force F between the dipoles can be found by taking the derivative of the potential energy with respect to the distance r:
F=−dUdr
- Differentiating U:
F=−ddr(−14πϵ0⋅2p1⋅p2r3)
- This results in:
F=6p1⋅p24πϵ0r4
- The force is positive, indicating that the force is attractive since the potential energy is negative. Therefore, the nature of the force between the dipoles is attractive.
- The magnitude of the force between the two dipoles is:
F=6p1⋅p24πϵ0r4
- The nature of the force is attractive.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Advance MCQs40videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs33videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems107videos
GEOMETRICAL OPTICS
Similar Questions
Two short electric dipoles of moment P and 8P are placed in opposite direction on a line at a distance of 15cm.The electric field will be zero at point between the dipoles whose distance from the dipole of moment P is?
View SolutionTwo electric dipoles , each of dipole moment p=6.2×10−30 C m are placed with their axes along the same line their centre a distance d=10−8 m apart . Calculate the force of attraction between the dipoles .
View Solution
Knowledge Check
- Question 1 - Select One

Two point electric dipoles with dipole moment P1 and P2 are separated by a distance r with their dipole axes mutually perpendicular as shown. The force of interaction between the dipoles is (where k=14πε0)A2kP1P2r4B3kP1P2r3C4kP1P2r4D6kP1P2r4 - Question 2 - Select One
Two electric dipoles of moment p and 64p are placed in opposite direction on a line at a distance of 25cm. The electric field will be zero at point between the dipoles whose distance from the dipole of moment p is
A5cmB259cmC10cmD413cm - Question 3 - Select One
Find the force of interaction of two dipoles , if the two dipole moments are parallel to each other and placed at a distance x apart
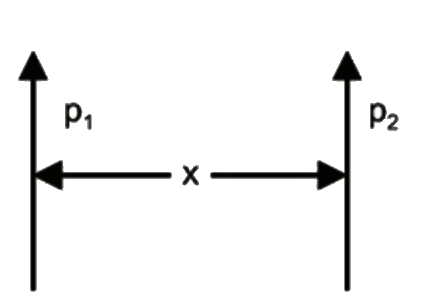 A3p1p24πε0x4Bp1p22πε0x4Cp1p24πε0x4Dp1p23πε0x4
A3p1p24πε0x4Bp1p22πε0x4Cp1p24πε0x4Dp1p23πε0x4
Two identical electric point dipoles have dipole moments −→P1=pˆiand−→P2=pˆi and are held on the x axis at distance 'a' from each other. When released, they move along the x-axis with the direaction of their dipole moments remaining unchanged. If the mass of each dipole is 'm', their speed when they are infinitely for apart is :
View SolutionTwo ideal electric dipoles A and B, having their dipole moment p1 and p2 respectively are placed on a plane with their centres at O as shown in the figure. At point C on the axis of dipole A, the resultant electric field is making an angle of 37∘ with the axis. The ratio of the dipole moment of A and B,p1p2 is : ( take sin37∘=35)
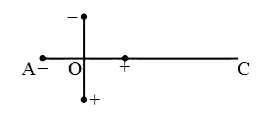 View Solution
View SolutionA short electric dipole (dipole moment P) is placed on the axis of a uniformly charged ring at a distance x from the centre as shown in figure. Radius of the ring is a and charge on it is Q.
Write the force on the dipole when x=a2 and when x=a. why the direction of force at two points is different?
(ii) is the force ont he dipole zero if x=0 ? if not where will you place the dipole so that force on it is zero.
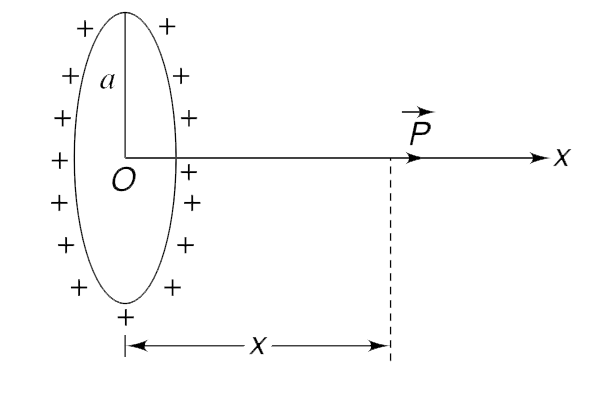 View Solution
View SolutionA very small electric dipole with dipole moment p is placed in such in way that it is at a distance r from another point charge +q. The point charge lies on the axis of the dipole . Electric dipole moment is pointing towards the point charge. Determine electric dipole will attract the point charge or repel it ? What will be the magnitude of force between them ?
View SolutionAn electric dipole of dipole moment p is placed in a uniform external electric field E. Then, the
View Solution

