Three point charges of 1C, 2C and 3C are placed at the . corners of an equilateral triangle of side 1m. Calculate the work required to move these charges to the corners of a smaller equilateral triangle of side 1.5m.
The correct Answer is:
To calculate the work required to move three point charges of 1C, 2C, and 3C from the corners of an equilateral triangle of side 1m to the corners of a larger equilateral triangle of side 1.5m, we can follow these steps:
Step 1: Calculate the Initial Potential Energy
The potential energy U of a system of point charges is given by the formula:
U=k∑i<jqiqjrij
where k is Coulomb's constant (k=9×109N m2/C2), qi and qj are the charges, and rij is the distance between the charges.
For the initial configuration (side length = 1m):
- The distances between each pair of charges are all 1m.
- The pairs of charges are (1C, 2C), (1C, 3C), and (2C, 3C).
Calculating the potential energy:
Uinitial=k((1)(2)1+(1)(3)1+(2)(3)1)
Uinitial=k(2+3+6)=k⋅11
Uinitial=11k=11×9×109J=99×109J
Step 2: Calculate the Final Potential Energy
For the final configuration (side length = 1.5m):
- The distances between each pair of charges are all 1.5m.
Calculating the potential energy:
Ufinal=k((1)(2)1.5+(1)(3)1.5+(2)(3)1.5)
Ufinal=k(21.5+31.5+61.5)
Ufinal=k(2+3+61.5)=k(111.5)
Ufinal=11k1.5=11×9×1091.5J=66×109J
Step 3: Calculate the Work Done
The work done W to move the charges is the difference between the final and initial potential energies:
W=Ufinal−Uinitial
W=(11k1.5−11k)
W=11k(11.5−1)=11k(1−1.51.5)=11k(−0.51.5)
W=−11k3=−11×9×1093J=−33×109J
Final Result
The work required to move the charges is:
W=−33×109J
This negative sign indicates that energy is released when moving the charges to the larger triangle configuration.
The potential energy U of a system of point charges is given by the formula:
U=k∑i<jqiqjrij
where k is Coulomb's constant (k=9×109N m2/C2), qi and qj are the charges, and rij is the distance between the charges.
- The distances between each pair of charges are all 1m.
- The pairs of charges are (1C, 2C), (1C, 3C), and (2C, 3C).
Uinitial=k((1)(2)1+(1)(3)1+(2)(3)1)
Uinitial=k(2+3+6)=k⋅11
Uinitial=11k=11×9×109J=99×109J
For the final configuration (side length = 1.5m):
- The distances between each pair of charges are all 1.5m.
Ufinal=k((1)(2)1.5+(1)(3)1.5+(2)(3)1.5)
Ufinal=k(21.5+31.5+61.5)
Ufinal=k(2+3+61.5)=k(111.5)
Ufinal=11k1.5=11×9×1091.5J=66×109J
The work done W to move the charges is the difference between the final and initial potential energies:
W=Ufinal−Uinitial
W=(11k1.5−11k)
W=11k(11.5−1)=11k(1−1.51.5)=11k(−0.51.5)
W=−11k3=−11×9×1093J=−33×109J
The work required to move the charges is:
W=−33×109J
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Advance MCQs40videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs33videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems107videos
GEOMETRICAL OPTICS
Similar Questions
Three points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionThree point charges 2μC,3μCand5μC are placed at the corners of an equilateral triangle of side 200 cm. Calculate the potentail energy of the system.
View Solution
Knowledge Check
- Question 1 - Select One
Three point charges 1C,2C and 3C are placed at the corners of an equilaternal triangle of side 1m. The work required to move these charges to the corners of a smaller equilaternal triangle of side 0.5m in two differenct ways as in fig. (A) and fig. (B) are Wa and Wb then:
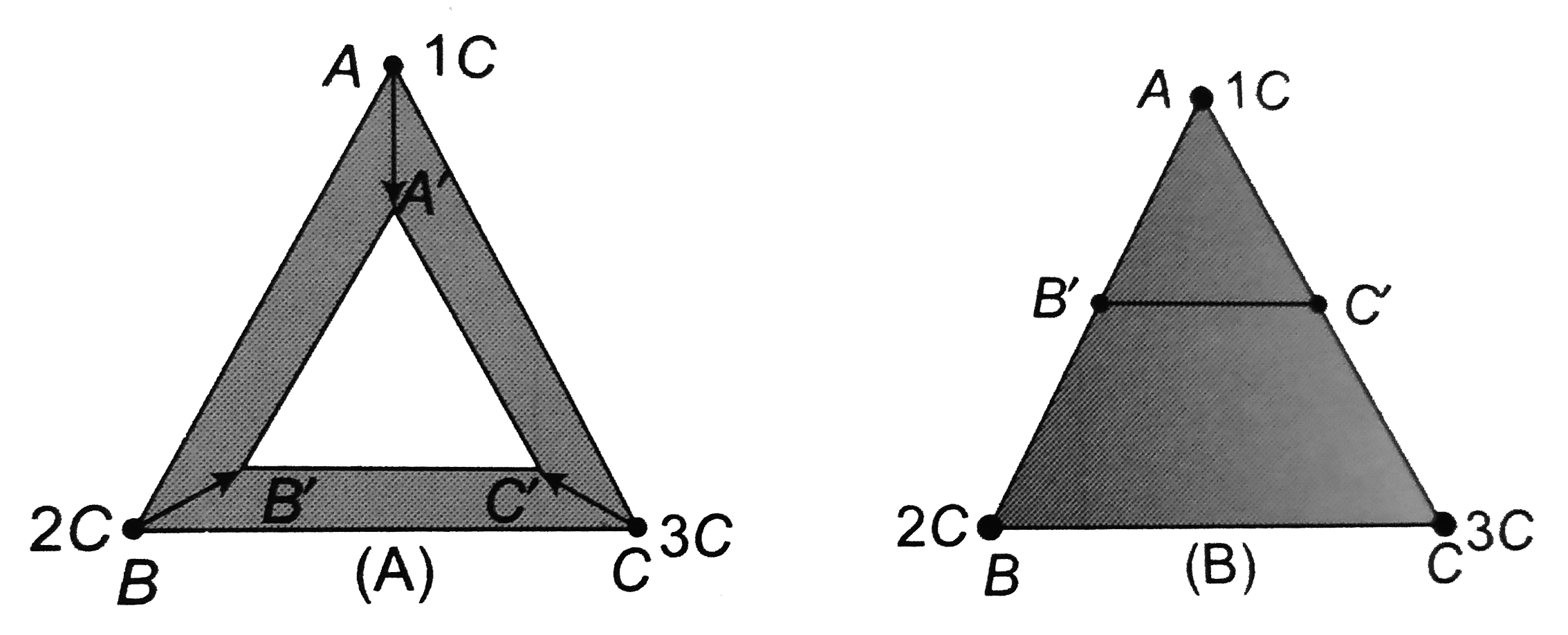 AWa>WbBWa<WbCWa=WbDWa=0 and Wb=0
AWa>WbBWa<WbCWa=WbDWa=0 and Wb=0 - Question 2 - Select One
Charge of 5μC each are placed at the corners of an equilateral triangle of side 10 cm. Then the force on each charge is :-
A78 NB39 NC29 ND22.5 N
Three points charges are placed at the corners of an equilateral triangle of side L as shown in the figure:
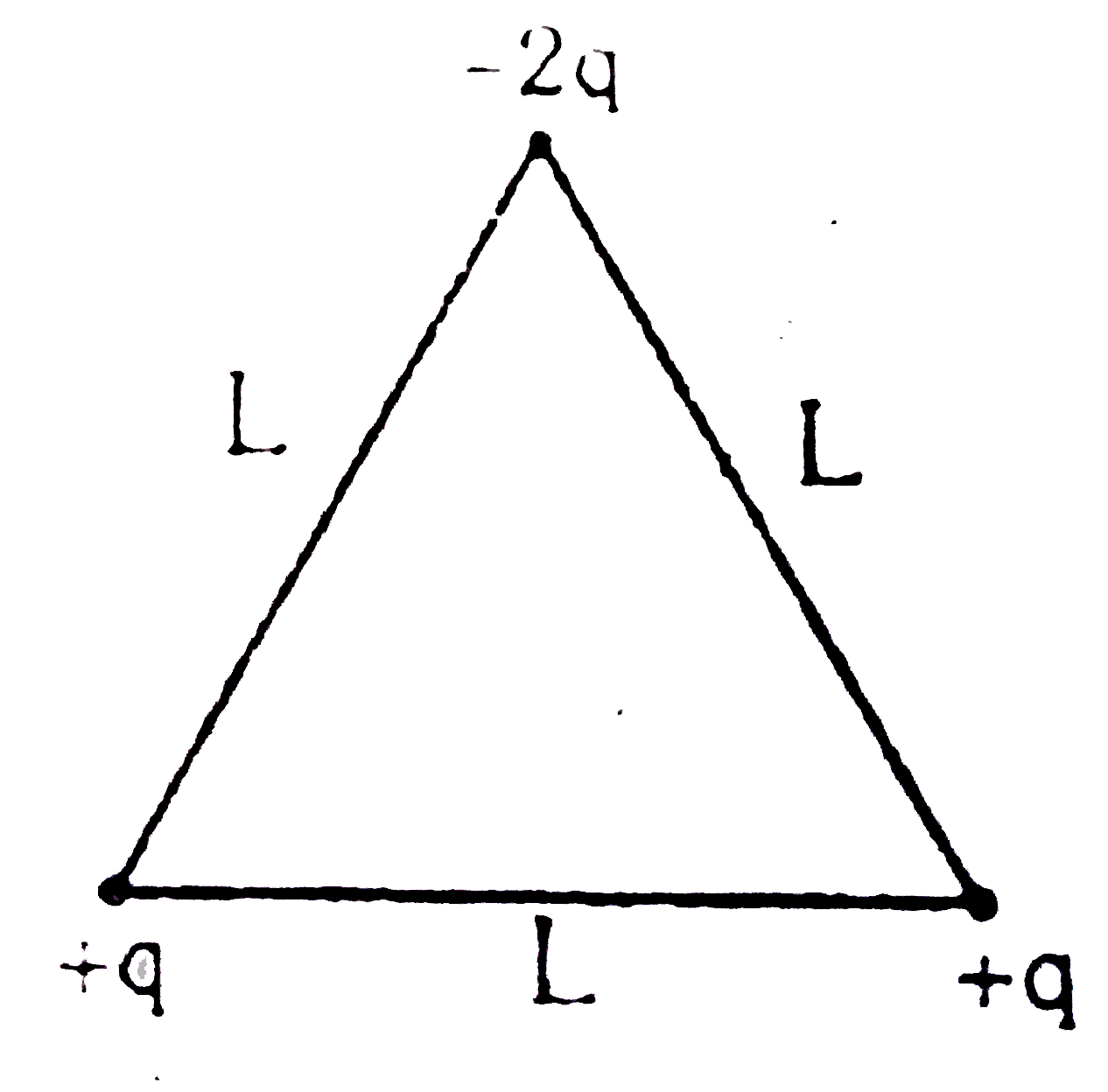 View Solution
View SolutionThree point charges 3nC, 6nC and 6nC are placed at the corners of an equilateral triangle of side 0.1 m. The potential energy of the system is
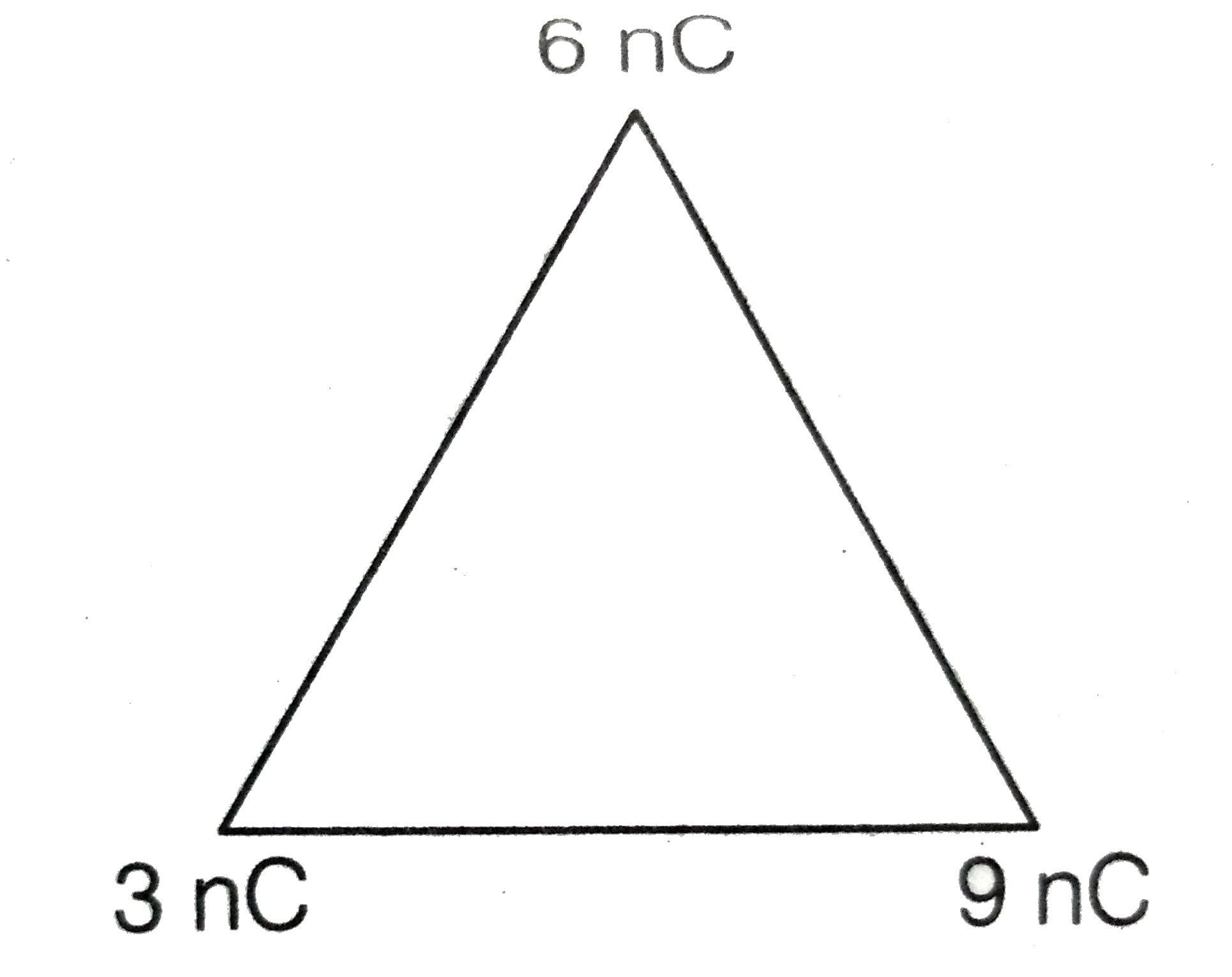 View Solution
View SolutionEqual charges of +4μC are placed at the three corners of an equilateral triangle of side 2m. Calculate the magnitude and direction of the force on one of the charges.
View SolutionThree charges of 1 nC, 2 nC and 3 nC are placed at the corners of an equilateral triangle of side √3m. Calculate electrostatic potential at a point equidistant from the three corners of the triangle.
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionA charge of 0.5 nC is placed at the centre of an equilateral triangle of side 10 cm. Calculate the potential at all the three vertices of the triangle.
View Solution

