A gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion ( in the intermediate stages of expansion/ compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=-PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process, since
P=nRTV,so,
w=∫dw=−∫VfVinRTV.dV=−nRT In(VfVi)
Since,dw=PdV, so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
In the above problem:
work done by gas Ist sample > work done by gas in Iind sample
work done by gas in Iind sample > work done by gas in Ist sample
work done by gas Ist sample=work done by gas in Iind sample
none of the above
The correct Answer is:a
Topper's Solved these Questions
Similar Questions
A gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different process.
I: by isothermal irreversible process
II: by reversible process having equation P2V= constant
III. by reversible adiabatic process
IV. by irreversible adiabatic expansion against constant external pressure.
Then, in the graph shown in the final state is represented by four different points then, the correct match can be
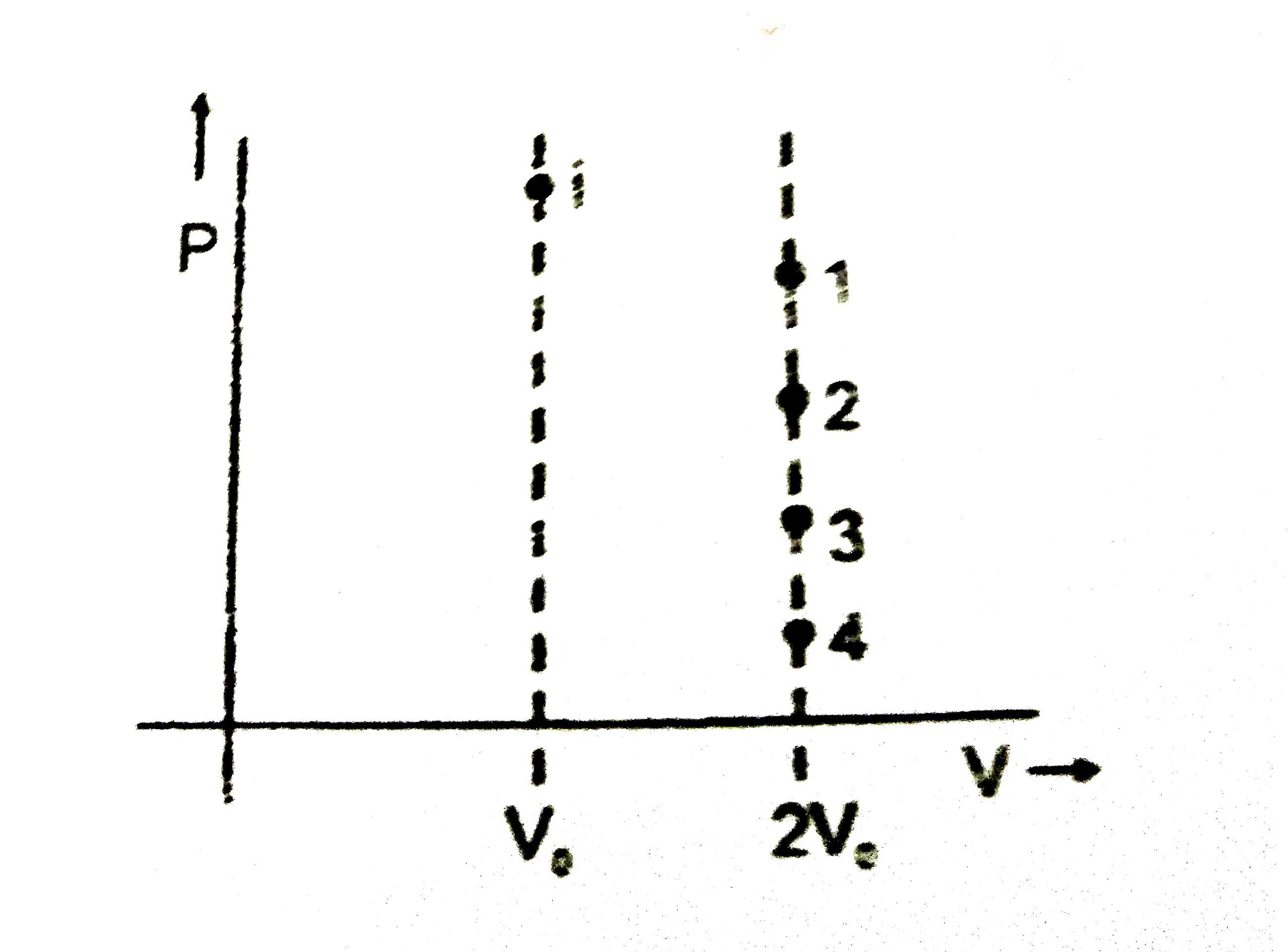
View SolutionA gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion ( in the intermediate stages of expansion/ compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=-PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process, since
P=nRTV,so,
w=∫dw=−∫VfVinRTV.dV=−nRT In(VfVi)
Since,dw=PdV, so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
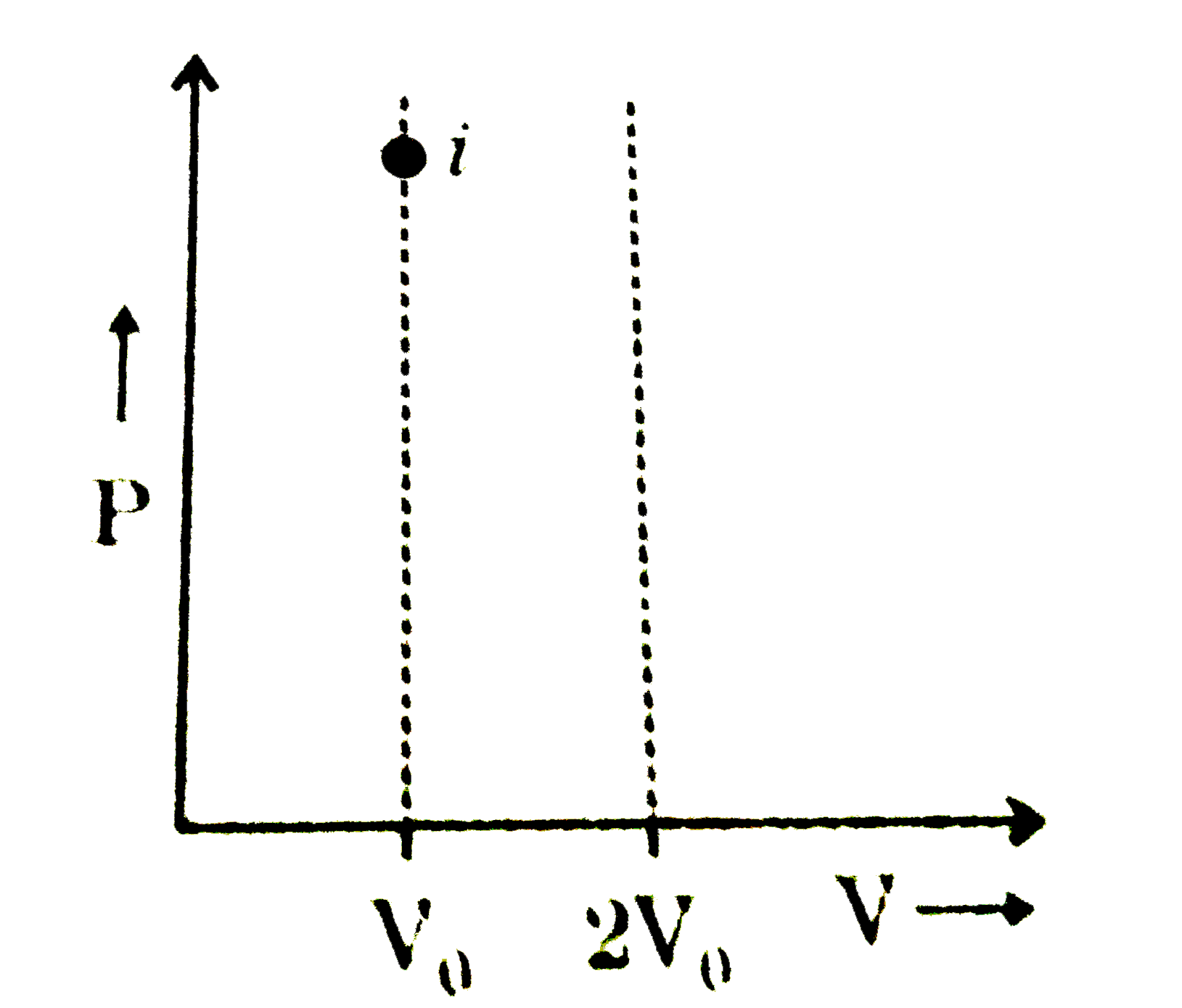
Two samples (initially under same states) of an idea gas are first allowed to expand to doubletheir volume using irreversible isothermal expansion against constant external pressure, then samples are turned back to their original volume first by reversible process having equation PV2= constant then:
View Solution
Knowledge Check
A gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion ( in the intermediate stages of expansion/ compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=-PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process, since
P=nRTV,so,
w=∫dw=−∫VfVinRTV.dV=−nRT In(VfVi)
Since,dw=PdV, so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
There are two sample of same gas initially at same initial state. Gases of both the sample are expanded. Ist sample using reversible isothermal process and IInd sample using reversible adiabatic process till final pressures of both the samples become half of the initial pressure , then :AFinal volume of Ist sample < final volume of Iind sampleBfinal volume of IInd sample < final volume of Ist sampleCfinal volumes will be equalDinformation insufficientA gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion ( in the intermediate stages of expansion/ compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=-PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process, since
P=nRTV,so,
w=∫dw=−∫VfVinRTV.dV=−nRT In(VfVi)
Since,dw=PdV, so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
An ideal gaseous sample at time state i(P0V0T0) is allowed to expand to volume 2V0 using two different processes, in the first process the equation of process is PV2=K1 and in second process the equation of the process is PV=K2. Then :Awork done in the first process will be greater than work in second process ( magnitude wise)Bthe order of values of work done cannot be compared unless we know the value of K1 and K2Cvalue of work done ( magnitude) in second process is greater in above expansion irrespective of the value of K1 and K2D1st process is not possibleA gaseous sample is generally allowed to do only expansion/compression type of work against its surroundings. The work done in case of an irreversible expansion ( in the intermediate stages of expansion/ compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=-PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process, since
P=nRTV,so,
w=∫dw=−∫VfVinRTV.dV=−nRT In(VfVi)
Since,dw=PdV, so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different processes.

(P)By isothermal irreversible process
(Q) By reversible process having equation P2V= constant
(R) By reversible adiabatic process
(S)By irreversible adiabatic expansion against constant external pressure. Then in the graph shown the final state is represented by four different points then, the correct match can be :A1−P,2−Q,3−R,4−SB1−Q,2−P,3−S,4−RC2−R,3−Q,4−P,1−SD3-Q,1-P,2-S,4-R
A gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
In the above problem
View SolutionA gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different process.
I: by isothermal irreversible process
II: by reversible process having equation P2V= constant
III. by reversible adiabatic process
IV. by irreversible adiabatic expansion against constant external pressure.
Then, in the graph shown in the final state is represented by four different points then, the correct match can be
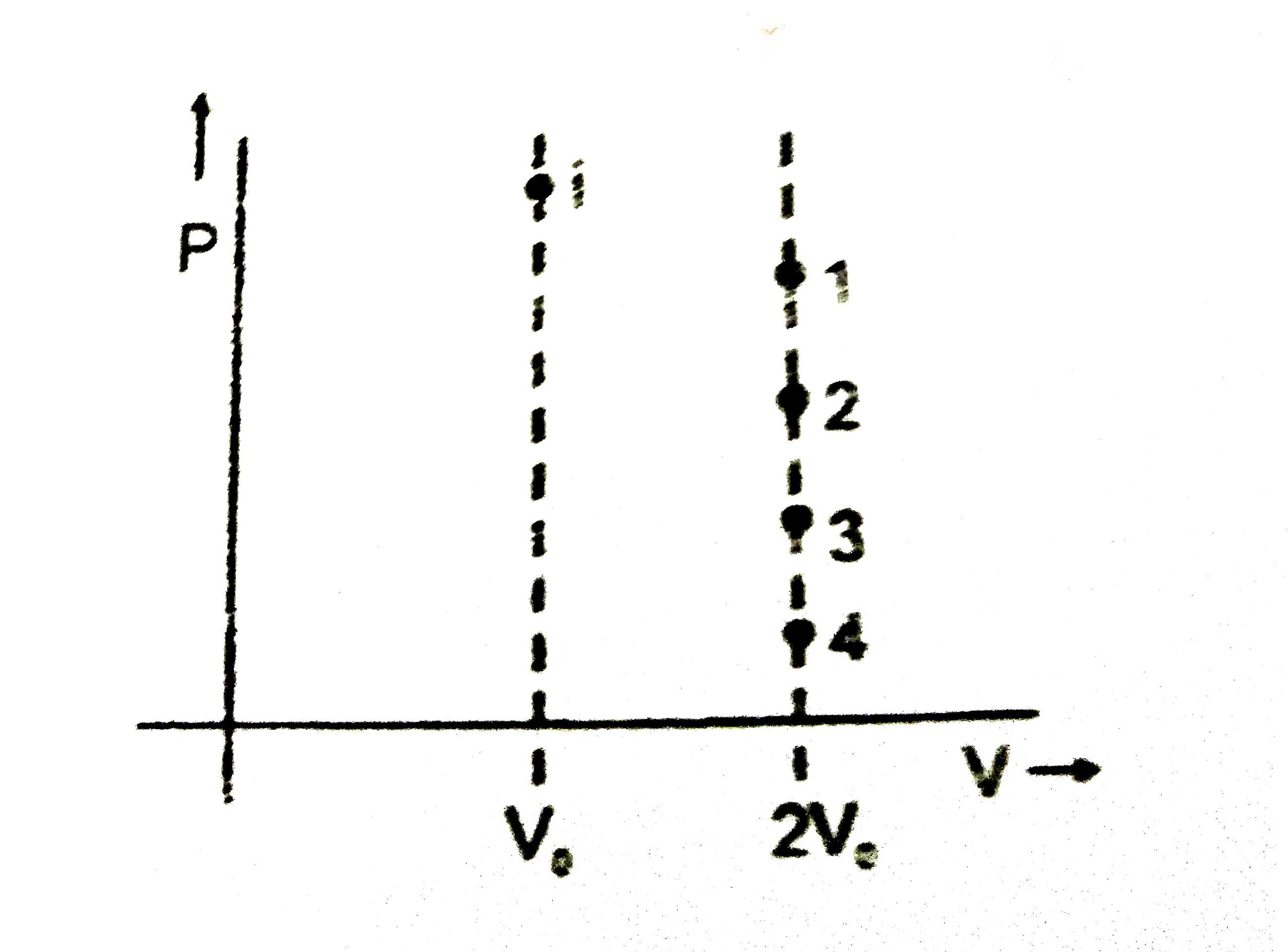
View SolutionWork done in a reversible expansion is
View SolutionThe work done in an isothermal reversible expansion of n moles of a gas is
View SolutionWork done in reversible isothermal expansion is given by
View Solution
