One mole of an ideal monoatomic gas at 27∘C undergoes the process in which TαV3. Then calculate the heat absorbed (in calories) when gas doubles it's volume (R=2cal//mol−K)
The correct Answer is:7700
To solve the problem step by step, we will follow the provided information and apply the relevant thermodynamic principles.
Step 1: Understand the Given Information
We have one mole of an ideal monoatomic gas at an initial temperature of 27∘C (which is 300K). The gas undergoes a process where the temperature T is proportional to the volume V cubed, i.e., T∝V3. We need to calculate the heat absorbed when the volume of the gas doubles.
Step 2: Determine Initial and Final Temperatures
Since the volume doubles, we can express this mathematically:
- Let the initial volume be V1.
- The final volume will be V2=2V1.
From the relationship T∝V3:
T2T1=(V2V1)3=(2)3=8
Thus, we can find T2:
T2=8×T1=8×300K=2400K
Step 3: Use the Ideal Gas Law
The ideal gas law is given by:
PV=nRT
For our case, we can express the temperature in terms of pressure and volume:
T=PVnR
Since n=1 mole and R=2cal/mol-K, we can write:
T∝V3⟹PV∝V3⟹PVn=constant
Here, we need to find n. From the relation PVn=constant, we can deduce that:
n=−2
Step 4: Calculate the Heat Capacity
For a monoatomic ideal gas, the heat capacities are:
CV=32RandCP=52R
The effective heat capacity C for the process can be calculated using:
C=CV+R1−n
Substituting CV and n:
C=32R+R1−(−2)=32R+R3
Finding a common denominator (which is 6):
C=9R6+2R6=11R6
Step 5: Calculate the Heat Absorbed
Using the formula for heat absorbed:
Q=nCΔT
Where:
- n=1 mole
- C=11R6
- ΔT=T2−T1=2400K−300K=2100K
Substituting the values:
Q=1×11R6×2100
Substituting R=2cal/mol-K:
Q=11×26×2100=226×2100=22×21006=7700calories
Final Answer
The heat absorbed when the gas doubles its volume is Q=7700calories.
---
We have one mole of an ideal monoatomic gas at an initial temperature of 27∘C (which is 300K). The gas undergoes a process where the temperature T is proportional to the volume V cubed, i.e., T∝V3. We need to calculate the heat absorbed when the volume of the gas doubles.
Since the volume doubles, we can express this mathematically:
- Let the initial volume be V1.
- The final volume will be V2=2V1.
T2T1=(V2V1)3=(2)3=8
Thus, we can find T2:
T2=8×T1=8×300K=2400K
The ideal gas law is given by:
PV=nRT
For our case, we can express the temperature in terms of pressure and volume:
T=PVnR
Since n=1 mole and R=2cal/mol-K, we can write:
T∝V3⟹PV∝V3⟹PVn=constant
Here, we need to find n. From the relation PVn=constant, we can deduce that:
n=−2
For a monoatomic ideal gas, the heat capacities are:
CV=32RandCP=52R
The effective heat capacity C for the process can be calculated using:
C=CV+R1−n
Substituting CV and n:
C=32R+R1−(−2)=32R+R3
Finding a common denominator (which is 6):
C=9R6+2R6=11R6
Using the formula for heat absorbed:
Q=nCΔT
Where:
- n=1 mole
- C=11R6
- ΔT=T2−T1=2400K−300K=2100K
Q=1×11R6×2100
Substituting R=2cal/mol-K:
Q=11×26×2100=226×2100=22×21006=7700calories
The heat absorbed when the gas doubles its volume is Q=7700calories.
Topper's Solved these Questions
Similar Questions
One mole of an ideal monoatomic gas at 1 atm, 300 K undergo a process in which pressure of gas is 8 atm then calculate W (in cal).
View SolutionOne mole of an ideal monoatomic gas undergoes the following cyclic process. Calculate the magnitude of work (in cal) in a cycle. (Use: ln 2 = 0.7)

View Solution
Knowledge Check
One mole of a monoatomic ideal gas undergoes a thermodynamic process such thatV3T2= constant. Then,
Awork done by the gas is 200R when temperature of the gas is raised by 300 KBthe specific heat of the gas in the process is 136RCwork done by the gas is 300R when temperature of the gas maised by 600 KDthe specific heat of the gas in the process is 214 ROne mole of an ideal monoatomic gas undergoes a described by the equations PV3= constant The heat the gas during this process is :
A2RBRC32RD53ROne mole of an ideal monoatomic gas under goes a process V=aT2. The temperature of the gas increases by 100K. Which of the following is incorrect ?
Athe work done by the gas in the process is 200R JouleBthe molar heat capacity for the process is 7R2Cfor the process PT2= constantDfor the process coefficient of volume expansion is γ=2T
One mole of a monoatomic ideal gas undergoes the process A→B in the given P-V diagram. What is the specific heat for this process?
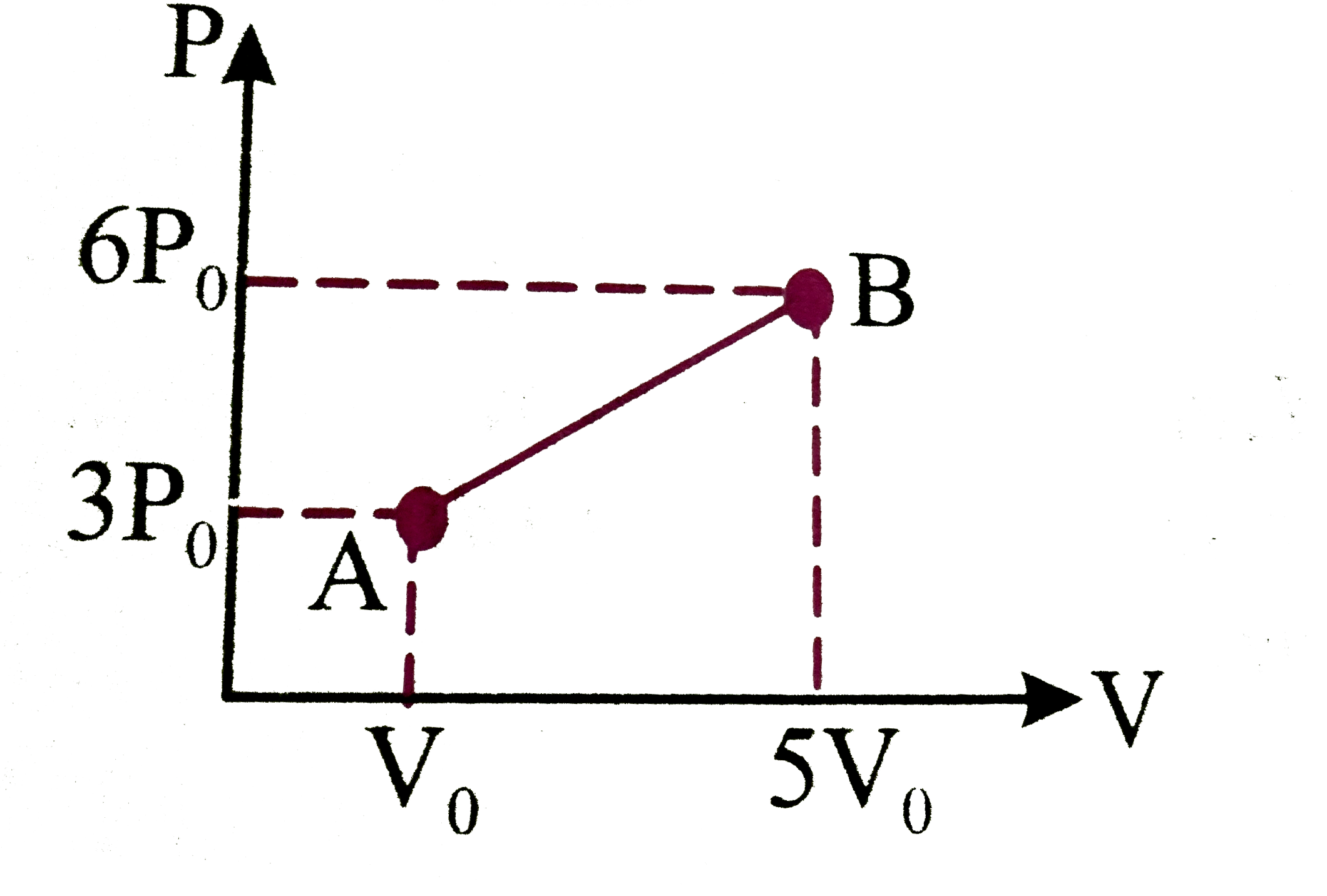
View SolutionOne mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
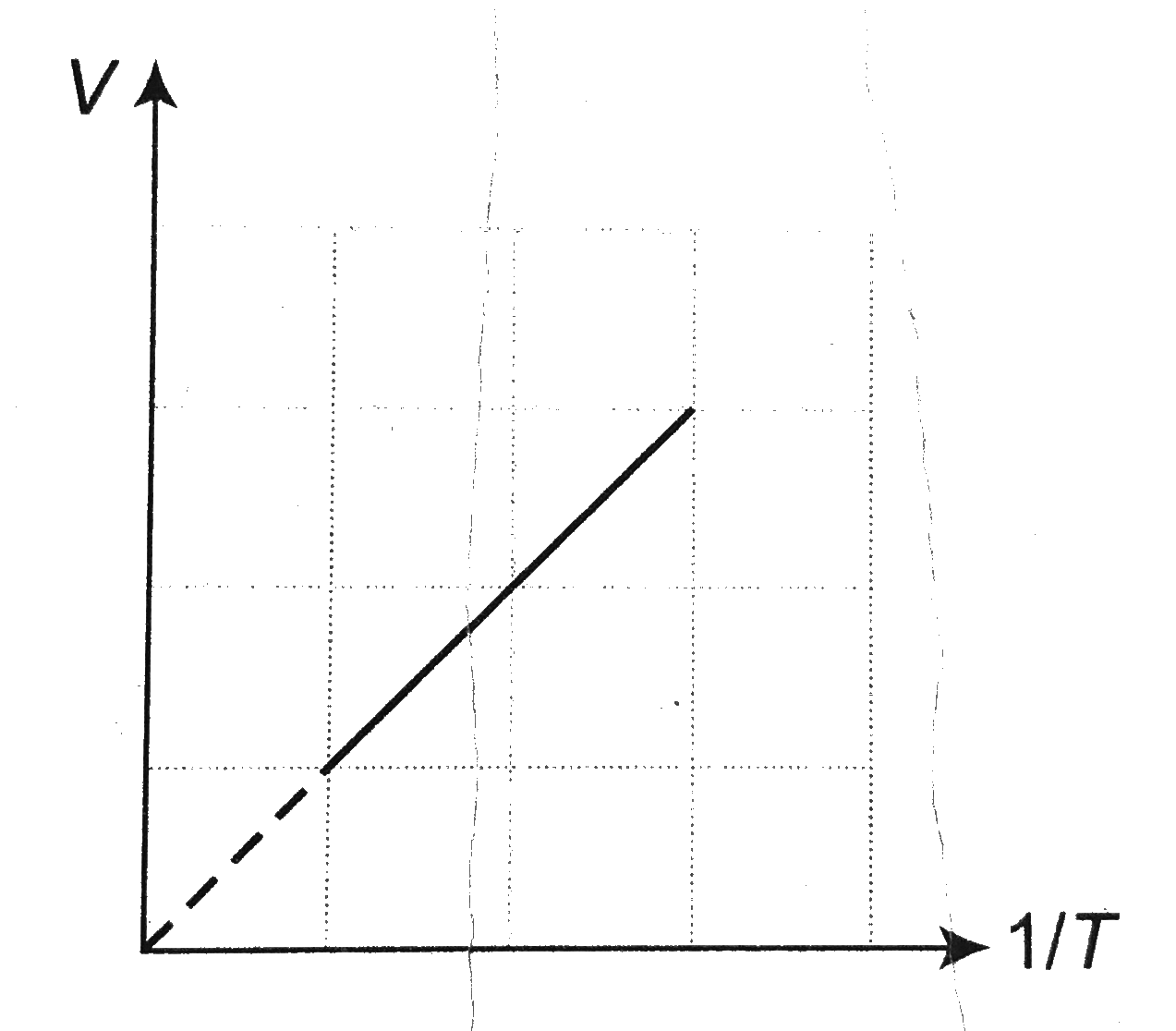
R is a gas constant.
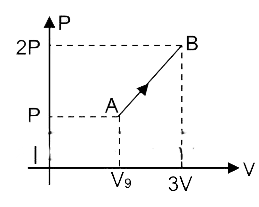
View SolutionOne mole of a monoatomic ideal gas undergoes process AB in given P – V diagram then average specific heat for this process is:
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process as shown in figure. Then the change in the energy in expanding the gas from a to c along the path abc is:

View SolutionAn ideal monoatomic gas undergoes a cyclic process ABCA as shown in the figure. The ratio of heat absorbed during AB to the work done on the gas during BC id
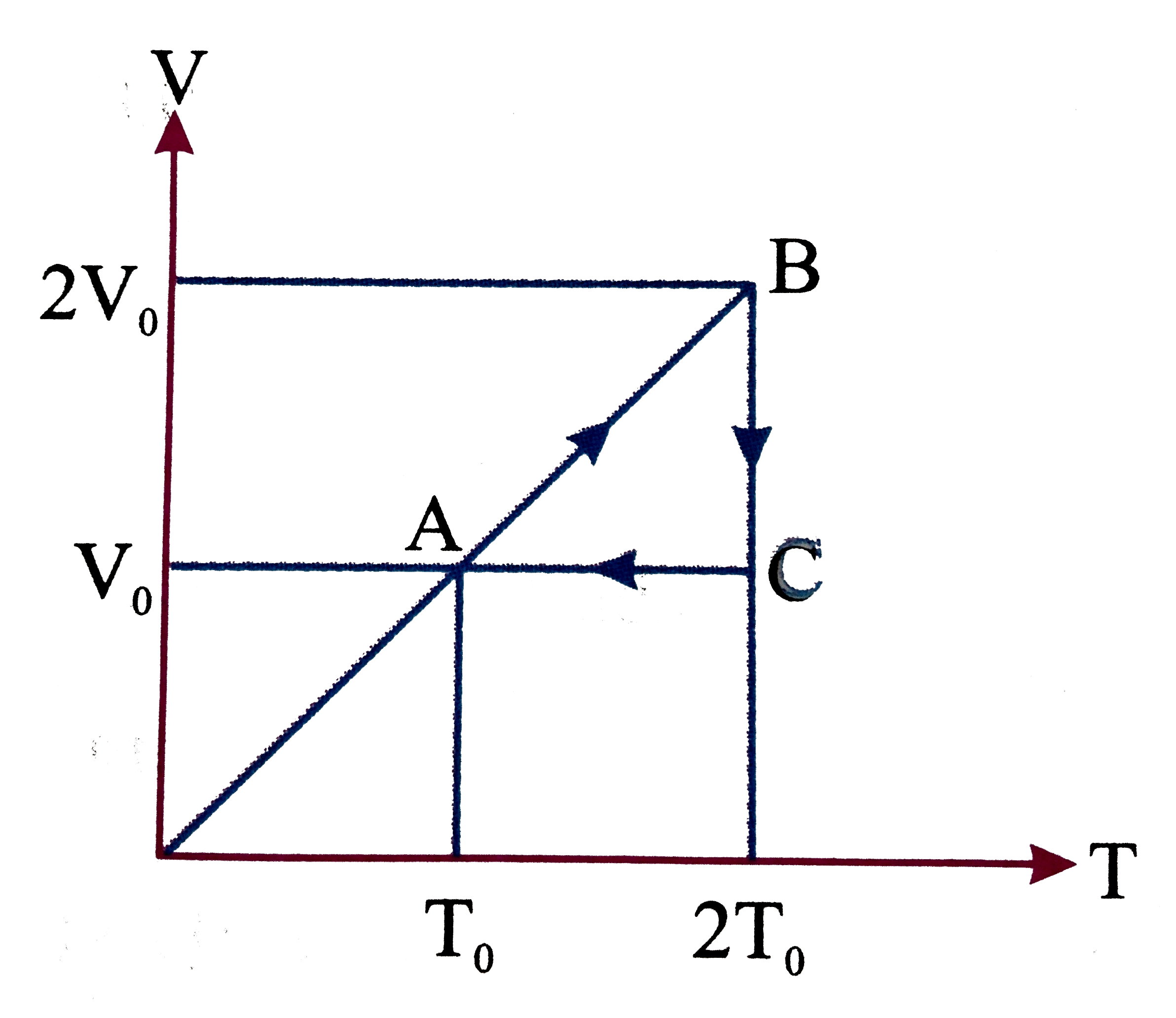
View Solution
