A uniform rectangular block of dimensions shown in fig is sliding on the horizontal surface with a velocity v when it strikes a small kerb in the surface. Determine the minimum value of v for which the block will pivot about the kerb and just reach the vertical position with no velocity. Assume negligible rebound at the step.

Step by step video & image solution for A uniform rectangular block of dimensions shown in fig is sliding on the horizontal surface with a velocity v when it strikes a small kerb in the surface. Determine the minimum value of v for which the block will pivot about the kerb and just reach the vertical position with no velocity. Assume negligible rebound at the step. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE83videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE41videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
A uniform block of mass M and dimensions as shown in the figure is placed on a rough horizontal surface and given a velocity V0 to the right. A is a point on the surface to the left of the block.
(a) Write the angular momentum of the block about point A just after it begins to move
(b) Due to friction the block stops. What happened to its angular momentum about point A? Which torque is responsible for change in angular momentum of the block?
 View Solution
View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
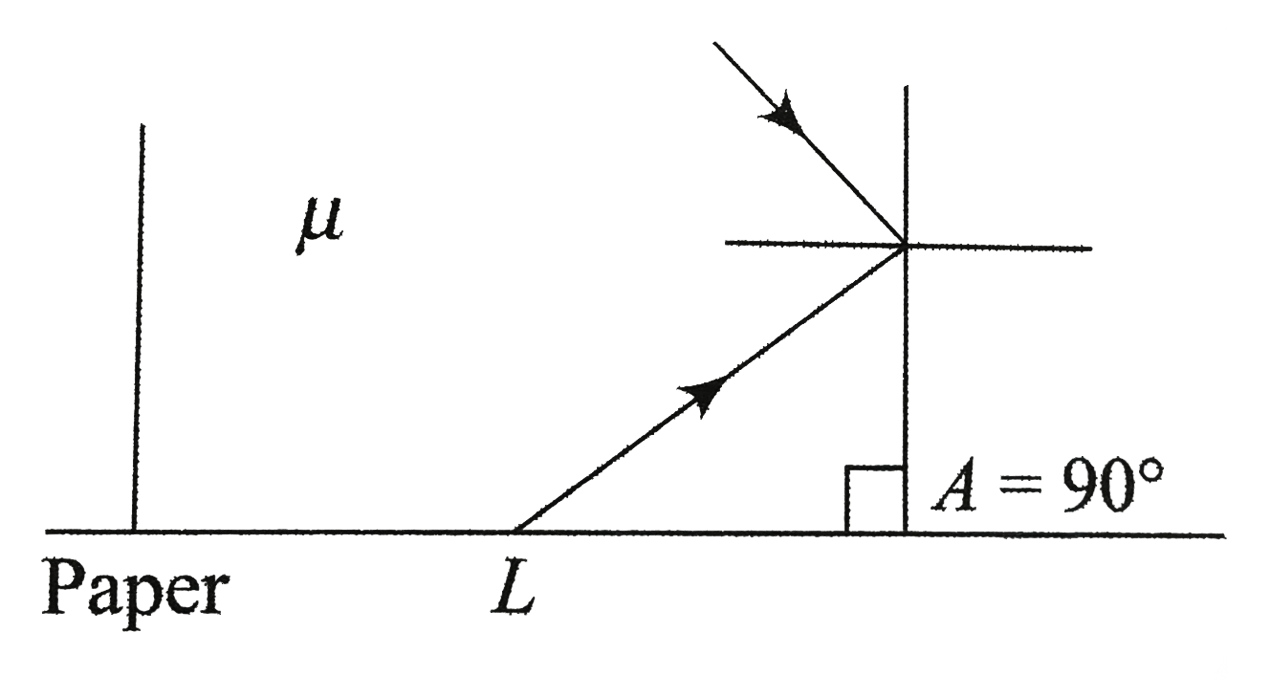 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
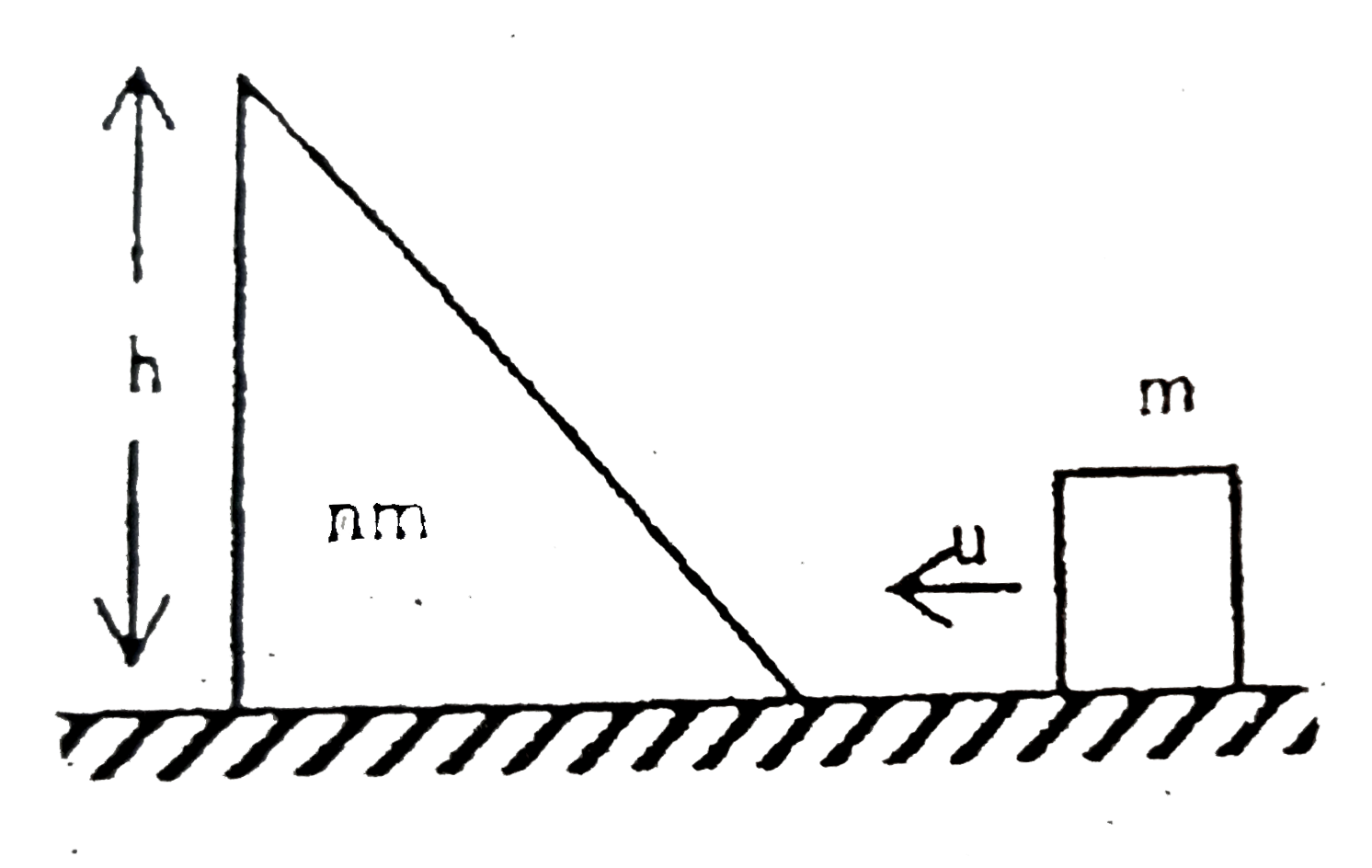 A√2ghBn2ghC√2gh(1+1n)D√2gh(1−1n)
A√2ghBn2ghC√2gh(1+1n)D√2gh(1−1n) - Question 2 - Select One
A block of mass m is pushed towards the movable wedge of mass M and height h, with a velocity v0. All surfaces are smooth . The minimum value of v0 for which the block will reach the top of the wedge is
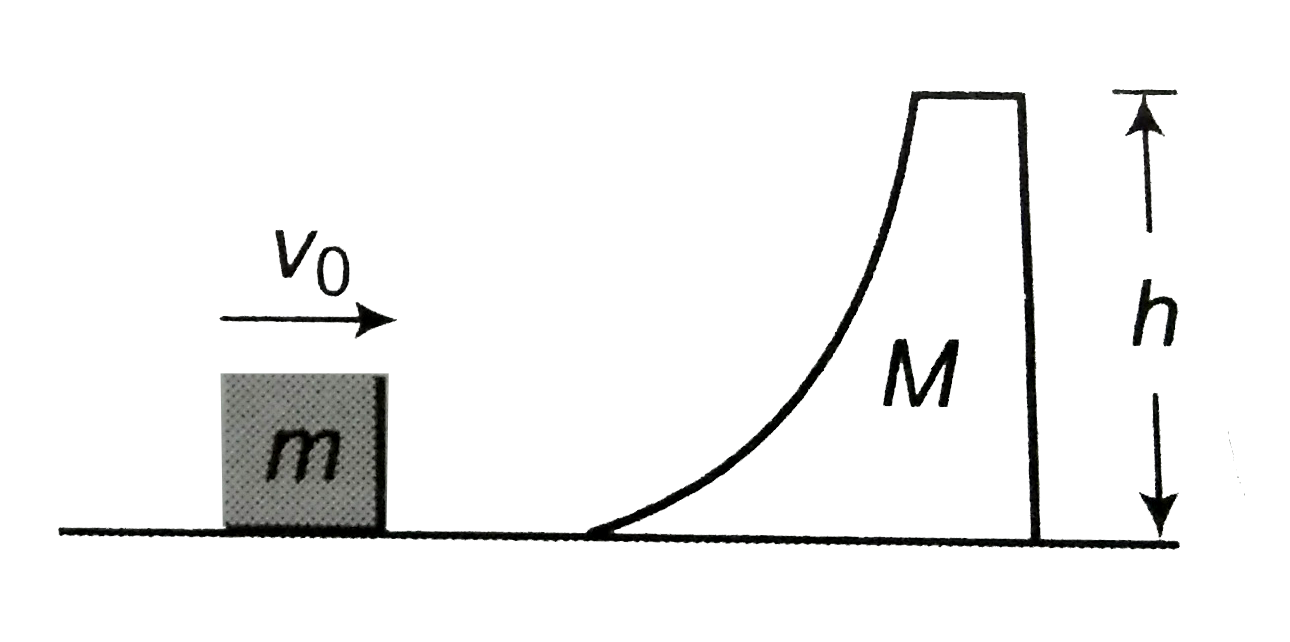 A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M)
A√2ghB√2ghmMC√2gh(m+M)MD√2ghm(m+M) - Question 3 - Select One
A small block of mass m is pushed towards a movable wedge of mass ηm and height h with initial velocity u.All surface are smooth. The minimum value of u for which the block will reach the top of the wedge:
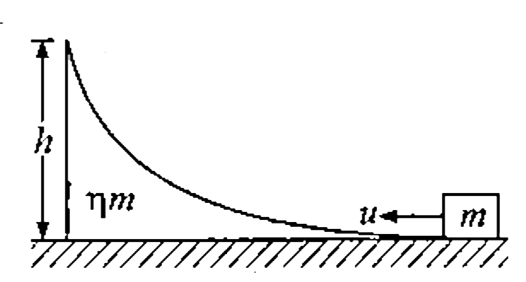 A√2gh(1+1h)B√(1+12gh)nC√n2ghD√1+h2gh
A√2gh(1+1h)B√(1+12gh)nC√n2ghD√1+h2gh
A block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?
 View Solution
View SolutionA small block of mass m is pushed towards a movable wedge of mass ηm and height h with initial velocity u.All surface are smooth. The minimum value of u for which the block will reach the top of the wedge:
 View Solution
View SolutionA 15kg block is initially moving along a smooth horizontal surface with a speed of v=4m/s to the left. It is acted by a force F , which varies in the manner shown. Determine the velocity of the block at t=15 seconds.
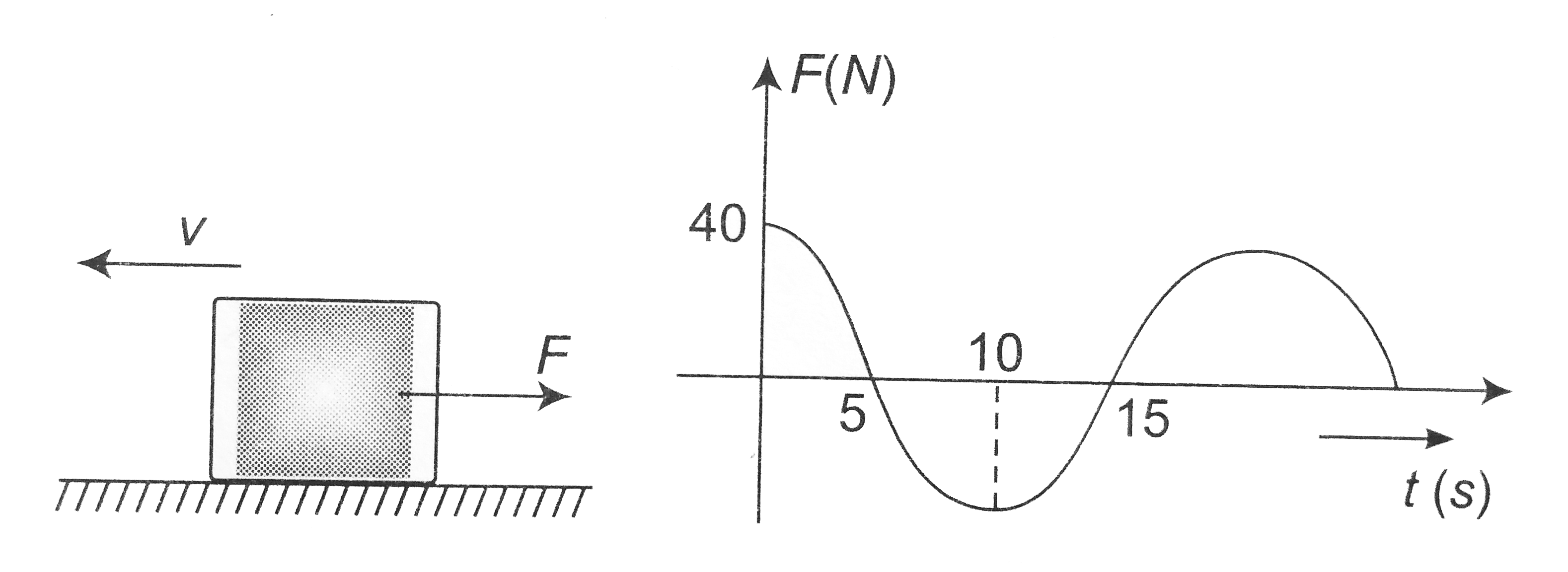 View Solution
View SolutionA block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
 View Solution
View SolutionA block of mass m is sliding down an inclined plane with uniform velocity v. Angle that the plane makes with the horizontal is θ. Assume edge of the cube to be a, calculate torque of the normal reaction about the centre of the block.
View Solution

