A heavy block of mass M hangs in equilibrium at the end of a rope of mass m and length l connected to a celling. Determine the tension in the rope at a distance x from the ceiling.
To determine the tension in the rope at a distance x from the ceiling, we can follow these steps:
Step 1: Understand the System
We have a heavy block of mass M hanging at the end of a rope of mass m and length l. The rope is attached to the ceiling, and we need to find the tension T in the rope at a distance x from the ceiling.
Step 2: Analyze the Free Body Diagram
Consider the section of the rope that is below the point at distance x from the ceiling. The length of this section of the rope is l−x. The weight of this section of the rope can be calculated as:
Weight of the rope section=(ml)(l−x)⋅g
where g is the acceleration due to gravity.
Step 3: Set Up the Equilibrium Condition
Since the block is in equilibrium, the sum of the forces acting on the section of the rope must be zero. The forces acting on this section are:
1. The tension T acting upwards.
2. The weight of the block M⋅g acting downwards.
3. The weight of the rope section (ml)(l−x)⋅g acting downwards.
Thus, the equilibrium condition can be expressed as:
T−(ml)(l−x)g−Mg=0
Step 4: Solve for Tension T
Rearranging the equilibrium equation gives us:
T=Mg+(ml)(l−x)g
This can be simplified to:
T=Mg+mg(l−x)l
Final Expression
The tension in the rope at a distance x from the ceiling is given by:
T=Mg+mg(l−x)l
We have a heavy block of mass M hanging at the end of a rope of mass m and length l. The rope is attached to the ceiling, and we need to find the tension T in the rope at a distance x from the ceiling.
Consider the section of the rope that is below the point at distance x from the ceiling. The length of this section of the rope is l−x. The weight of this section of the rope can be calculated as:
Weight of the rope section=(ml)(l−x)⋅g
where g is the acceleration due to gravity.
Since the block is in equilibrium, the sum of the forces acting on the section of the rope must be zero. The forces acting on this section are:
1. The tension T acting upwards.
2. The weight of the block M⋅g acting downwards.
3. The weight of the rope section (ml)(l−x)⋅g acting downwards.
T−(ml)(l−x)g−Mg=0
Rearranging the equilibrium equation gives us:
T=Mg+(ml)(l−x)g
This can be simplified to:
T=Mg+mg(l−x)l
The tension in the rope at a distance x from the ceiling is given by:
T=Mg+mg(l−x)l
Topper's Solved these Questions
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:level 1
Explore 103 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Level-2
Explore 73 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
- DESCRIPTION OF MOTIONBook:ANURAG MISHRAChapter:DESCRIPTION OF MOTIONExercise:Level-3
Explore 34 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:matching
Explore 3 Videos
Similar Questions
A uniform rope of mass m and length L is attached to the ceiling of a lift. The other end of the rope is attached to a block of mass M. The lift is moving up with a constant acceleration a0. Find the tension in the rope at a distance x from the ceiling as shown in the diagram.

View SolutionA uniform rope of length L is pulled by a constant force F. What is the tension in the rope at a distance l from the end where it is applied?
View Solution
Knowledge Check
A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
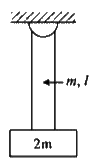
The speed of the pulseat the mid point of rope is:A√52glB√33glC√25glD√gl2A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
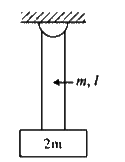
The time taken by the pulse to reach the other end of the rope is:A2√lg(√3−1)B2√lg(√3−2)C2√lgD2√lg(√3−√2)A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
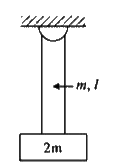
The wavelength of the pulse when it reaches the other end of the rope is :A√3λ0B√32λ0Cλ0Dλ02
A uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
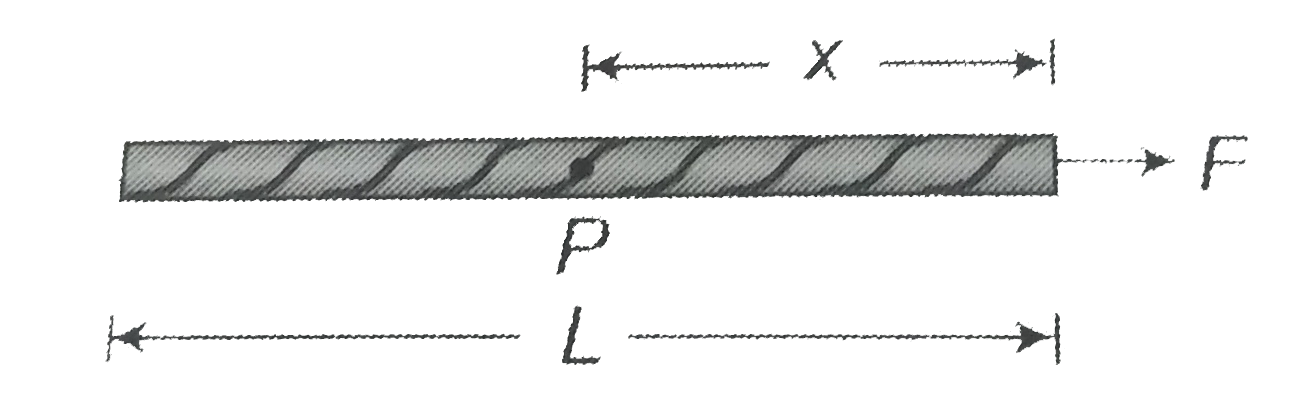
View SolutionA block of mass M is attached to a uniform rope of mass m. This arrangement is pulled by applying a force F at the rope as shown. Find the tension in the rope (a) at the junction of the rope and the block (b) at the mid point of the rope.
View SolutionA straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'I from that end is 9
View SolutionA 40-kg mass hanging at the end of a rope of length l. Oscillates in a vertical plane with an angular of θ0. What is the tension in the rope when it makes an angle θ with the vertial ? If the breaking strength of the rope is 80 kg, what is the maximum angular amplitude with which the mass can oscillate without the rope breaking ?
View SolutionA straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'l' from that end is
View Solution