The figure shows a block 'A' resting on a rough horizontal surface with μ=0.2. A man of mass 50 kg standing on the ground surface starts climbing the hanging ideal string. The maximum possible tension in the string is 1000N. The minimum time taken by the man to reach upto the pulley:
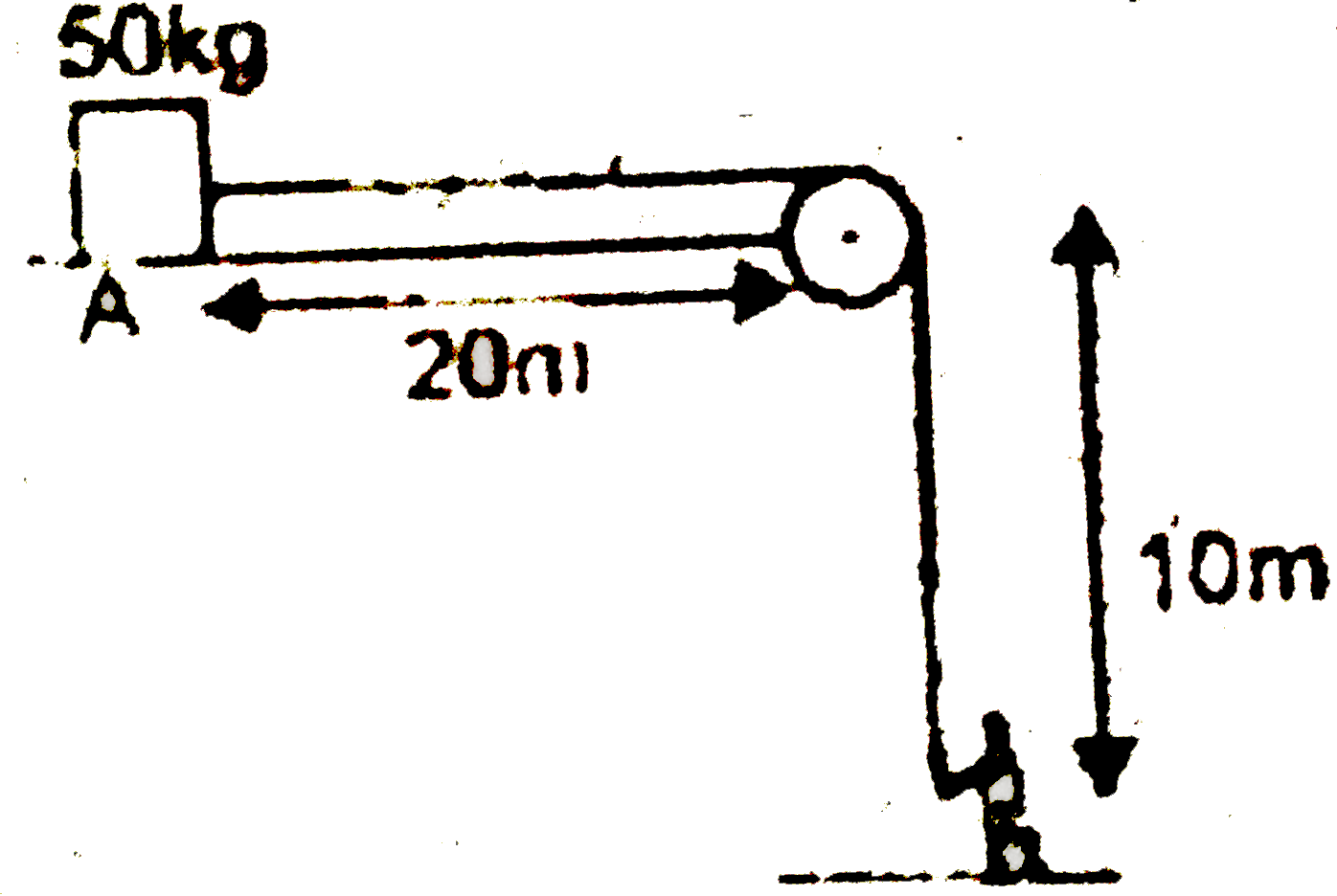
√2.5
1
√2
none of these
The correct Answer is:c
Topper's Solved these Questions
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-2
73 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-3
49 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Example
95 Videos
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-3
34 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
Similar Questions
A block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?
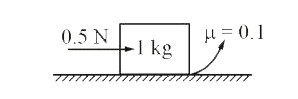
View SolutionA block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?

View Solution
Knowledge Check
A block of mass m and length l is kept at rest on a rough horizontal ground of friction coefficient μk. A man of mass m is standing at the right end. Now the man starts walking towards left and reaches the left end within time ‘t’. During this time, the displacement of the block is : (Assume the pressing force between the block and the ground remains constant and its value is same as it was initially. Also as sume that the block slides during the entire time (t))
 Al−μkgt22Bl+μkgt22Cμkgt2−l2Dl2
Al−μkgt22Bl+μkgt22Cμkgt2−l2Dl2A man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
 A2uBu2CzeroDu4
A2uBu2CzeroDu4A block of mass 100kg is kept on a horizontal rough surface. A man of mass 60kg is trying to pull the block with the help of ideal inextensible string. Find the minimum tension ( approximately ) in string to pull the block so that man remains at rest . Coefficient of friction between block and horizontal surface is 0.2 and that between man an horizontal surface is 0.5 ( g =10m/s2 )
A100NB166NC180ND196N
The figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
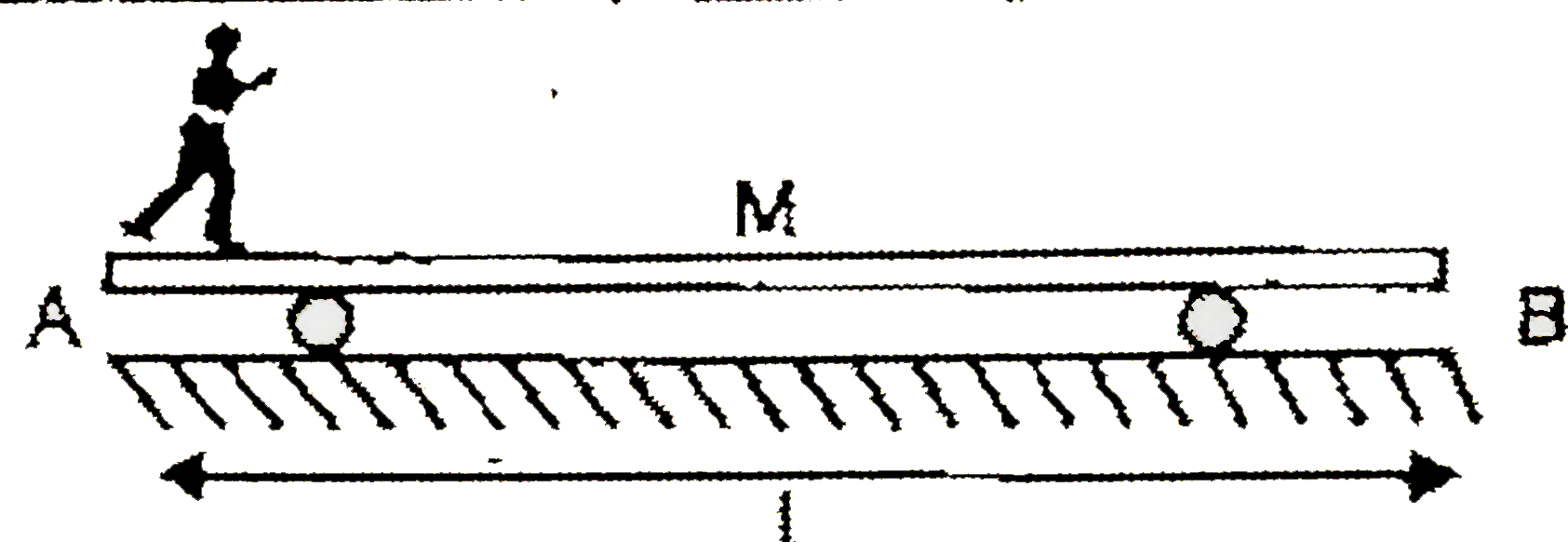
The time taken by the man to reach the other end is:
View SolutionA block of mass m and length l is kept at rest on a rough horizontal ground of friction coefficient μk. A man of mass m is standing at the right end. Now the man starts walking towards left and reaches the left end within time ‘t’. During this time, the displacement of the block is : (Assume the pressing force between the block and the ground remains constant and its value is same as it was initially. Also as sume that the block slides during the entire time (t))

View SolutionA body of mass 20kg is moving on a rough horizontal plane. A block of mass 3kg is connected to the 20 kg mass by a string of negligible mass through a smooth pulley as shown in the figure. The tension in the string is 27 N. The coefficient of kinetic friction between the heavier mass and the surface is (g = 10m/s2)
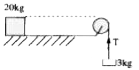
View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is

View SolutionA block of mass 100kg is kept on a horizontal rough surface. A man of mass 60kg is trying to pull the block with the help of ideal inextensible string. Find the minimum tension ( approximately ) in string to pull the block so that man remains at rest . Coefficient of friction between block and horizontal surface is 0.2 and that between man an horizontal surface is 0.5 ( g =10m/s2 )
View Solution
