Suppose a machine consists of a cage at the end of one arm The arm is hinged at O as shown in figure such that the cage revolves along a vertical circle of radius r at constant linear speed v=√gr. The cage is so attached that the man of weight W, standing on a weighing machine inside the cage, remains always vertical. Then :

The reading of his weight on the machine is equal to W at all positions
The weight reading at A is greater than the weight reading at E by 2W
The weight reading at G issame as that at C
The ratio of weight reading at E to that at A=0
The correct Answer is:b,c,d
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-349videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - level 1103videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-334videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
Similar Questions
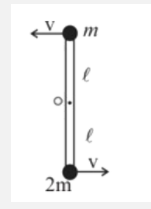
Two particles of masses m and 2m are attached to the massless rod of length 2l as shown in figure. The rod is hinged at its midpoint O and is free to rotate in vertical plane about hinge. The minimum speed v at the given instant so that it can complete the circle.
 View Solution
View SolutionTwo particles of masses m and 2m are attached to the massless rod of length 2l as shown in figure. The rod is hinged at its midpoint O and is free to rotate in vertical plane about hinge. The minimum speed v at the given instant so that it can complete the circle.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
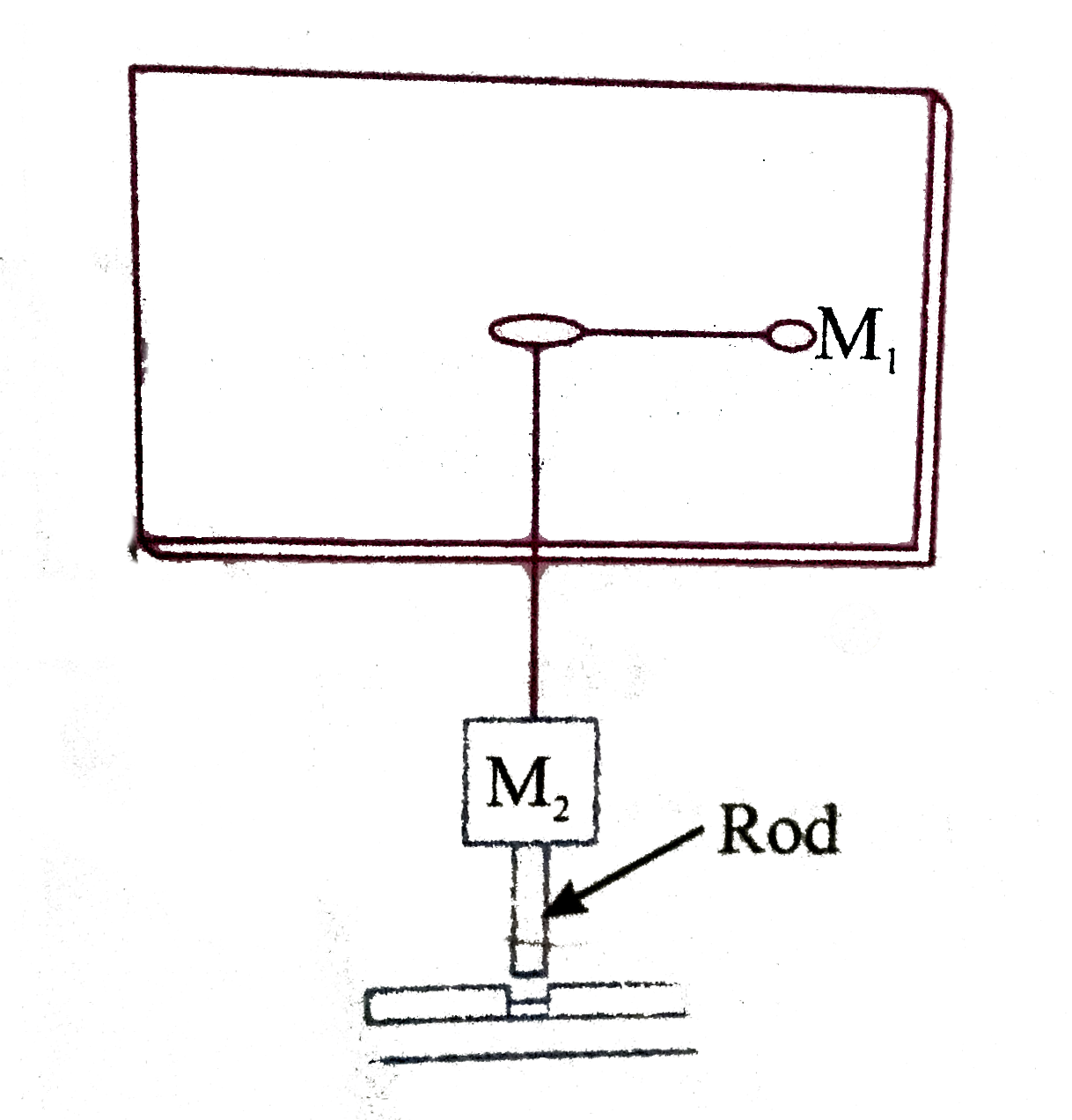
For the arrangement in the Figure, the particle M1 attached to one end of string which moves on a horizantal table in a circle of radius l2 (where l is the length of the string) with constant angular speed ω. The other end of the string attached to to mass M2 which rest on a vertical rod. When the rod collapse, the acceleration of mass M2 at that instant
 AgBω2l2C2M2g−M1lω22(M1+M2)DM2g+M1lω2M1+M2
AgBω2l2C2M2g−M1lω22(M1+M2)DM2g+M1lω2M1+M2 - Question 2 - Select One
STATEMENT-1: One end of a string of length r is tied to a stone of mass m and the other end to a small pivot on a frictionless vertical board. The stone is whirled in a vertical circle with the pivot as the centre. The minimum speed the stone must have, when it is at the topmost point on the circle, so that the string does not slack is √gR.
because
STATEMENT-2: At the topmost point on the circle, the centripetal force is provided partly by tension in the string and partly by the weight of the stone.AStatement-1 is true, Statement-2 is True, Statement -2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True, Statement -2 is NOT a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement - 1 is False, Statement -2 is True.
For the arrangement in the Figure, the particle M1 attached to one end of string which moves on a horizantal table in a circle of radius l2 (where l is the length of the string) with constant angular speed ω. The other end of the string attached to to mass M2 which rest on a vertical rod. When the rod collapse, the acceleration of mass M2 at that instant
 View Solution
View SolutionA wheel of radius R=10cm and moment of inertia I=0.05kgm2 is rotating about a fixed horizontal axis O with angular velocity ω0=10rads−1. A uniform riigid rod of mass m=3kg and length l=50cm is hinged at one end A such that it can rotate at end A in a vertical plane. End B of the rod is tied with a thread as shown in figure such that the rod is horizontal and is just in contact with the surface of rotating wheel. Horizontal distance between axis of rotation O of cylinder and A is equal to a=30cm.
If the wheel stops rotating after one second after the thread has burnt, calculate coefficient of friction ,μ between the rod and the surface of the wheel. (g=10ms−2)
 View Solution
View SolutionA wheel of radius R=10cm and moment of inertia I=0.05kgm2 is rotating about a fixed horizontal axis O with angular velocity ω0=10rads−1. A uniform riigid rod of mass m=3kg and length l=50cm is hinged at one end A such that it can rotate at end A in a vertical plane. End B of the rod is tied with a thread as shown in figure such that the rod is horizontal and is just in contact with the surface of rotating wheel. Horizontal distance between axis of rotation O of cylinder and A is equal to a=30cm.
If the wheel stops rotating after one second after the thread has burnt, calculate coefficient of friction ,μ between the rod and the surface of the wheel. (g=10ms−2)
 View Solution
View SolutionTwo blocks A and B having mass m = 1 kg and M = 4 kg respectively are attached to a spring and placed vertically on a weighing machine as shown in the figure. Block A is held so that the spring is relaxed. A is released from this position and it performs simple harmonic motion with angular frequency w=25rads−1. The spring remains vertical
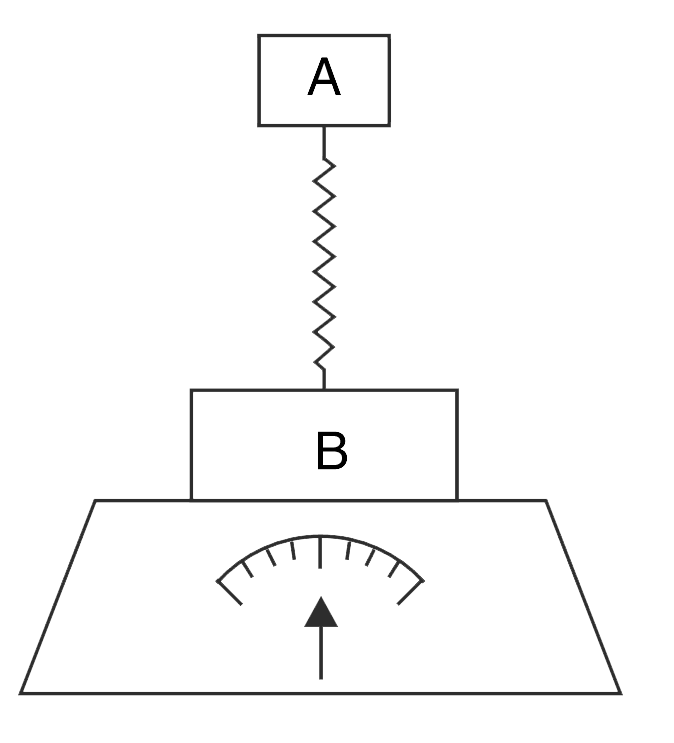
(a) Find the reading of the weighing machine as a function of time. Take t = 0 when A is released.
(b) What is the maximum reading of the weighing machine ?View SolutionIn a conical pendulum a small mass is revolving in horizontal circle with constant speed v at the end of the cord of length L that makes an angle θ with the vertical as shown . The value of angle θ would be (where r is the radius of circle)
 View Solution
View SolutionA small spherical marble of mass m and radius r is rolling without slipping on a rough track with speed v.The track further is in the shape of a vertical circle of radius R as shown in figure-5.144. With what minimum linear speed the marble is rolling so that it completely goes round the circle on the circular part of track.
 View Solution
View Solution

