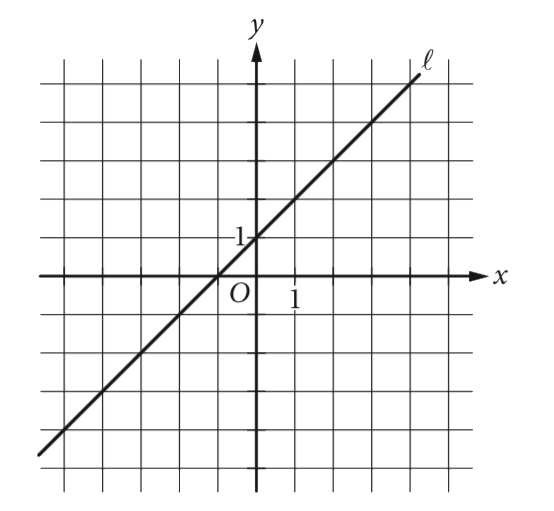
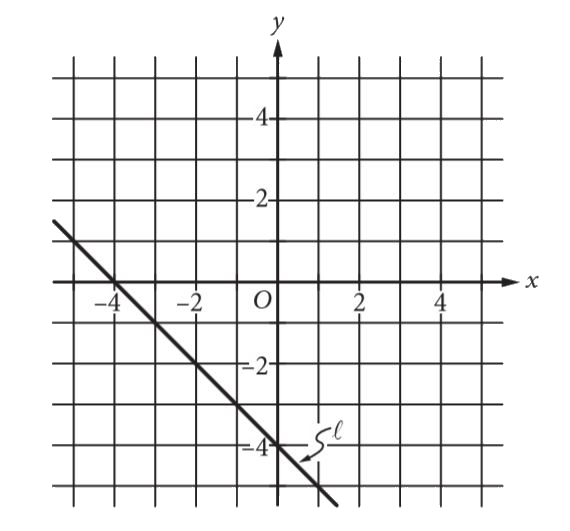
Which of the following equations has (have) graphes consisting of two perpendicular lines?
I. xy=0
II. |y|=|x|
III. |xy|=1
A
only I
B
only II
C
only III
D
only I and II
Video Solution
Text Solution
The correct Answer is:D
Graph I consists of the lines x=0 and y=0, which are the coodinate axes and are therefore perpendicular. Graph II consists of y=|x| and y=|x|, which are at ±45∘ to the coordinate axes and are therefore perpendicular. Graph III consists of the hypebolas xy=1 and xy=-1. Therefore, the correct answer choice is choice D.
There are two reasons why a graphing caculator solution is not recommended here. One is that equations, not functions, are given, and solving these equations so that they can be graphed involves two branches each. The other reason is that even with graphs, you would have to make judgments about perpendicularity. At a minimum, this would require you to graph the equations in a square window. [11]
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following is the graph of a line perpendicular to the line defined by the equation 2x+5y=10?
A B
B C
C D
D
- Question 2 - Select One
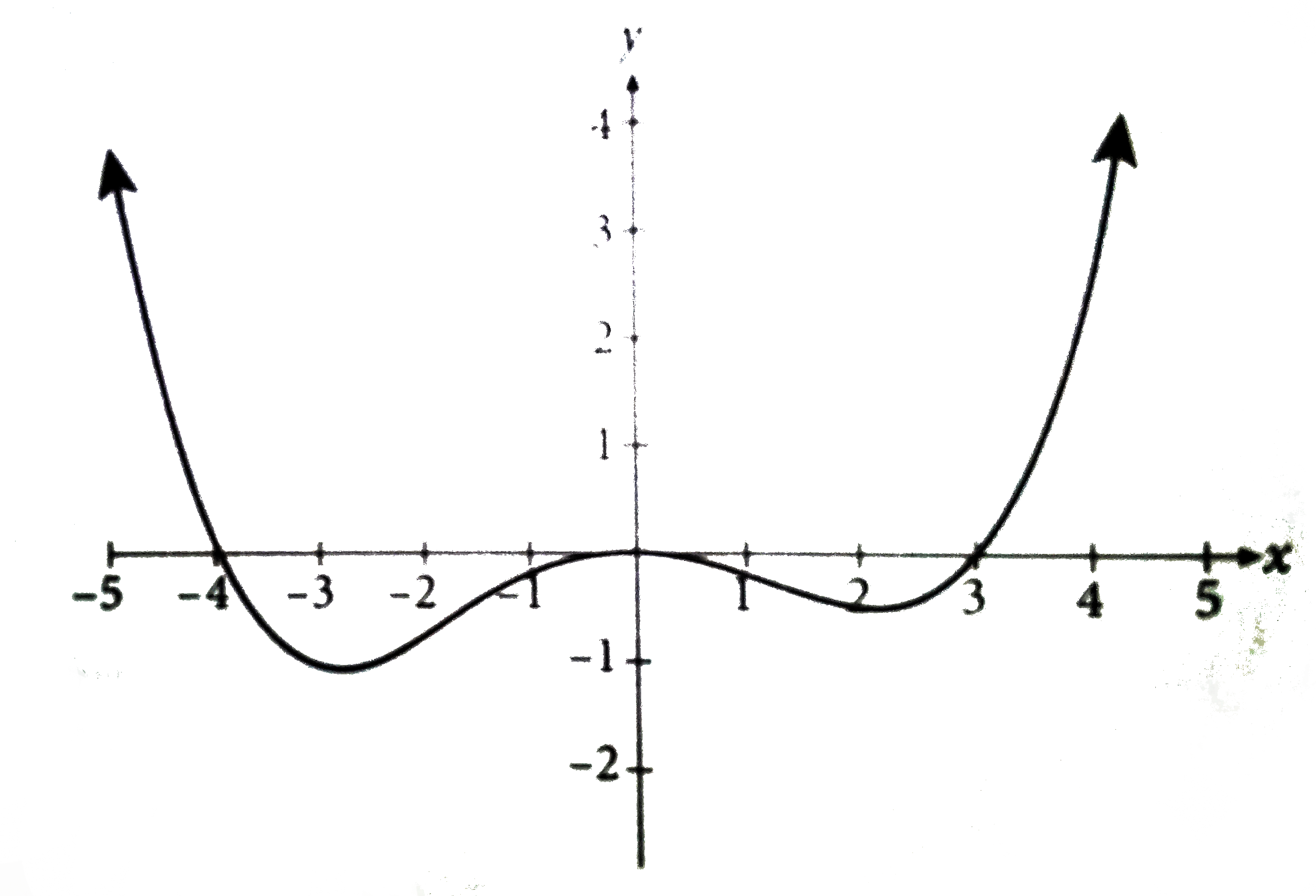
Which of the following could be the equation of the graph in the xy-plane shown above?Af(x)=x(x+3)(x−4)Bf(x)=x(x+4)(x−3)Cf(x)=x2(x+3)(x−4)Df(x)=x2(x+4)(x−3) - Question 3 - Select One
Which of the following equations has a graph in the xy-plane for which y is always greater than or equal to −1 ?
Ay=|x|−2By=x2−2Cy=(x−2)2Dy=x3−2
The equation 3ax2+9xy+(a2−2)y2=0 represents two perpendicular straight lines for
View SolutionWhich of the following equations have same graphs.
I.y=x−2
II.y=x2−4(x+2)
III.(x+2)y=x2−4View SolutionThe equation 2x2−3xy−py2+x+qy−1=0 represent two mutually perpendicular lines if
View SolutionWhich of the following is the graph of the equation y = 2x − 5 in the xy-plane?
View SolutionWhich of the following statements is true about the graph of the equation 2y − 3x = −4 in the xy-plane?
View Solution