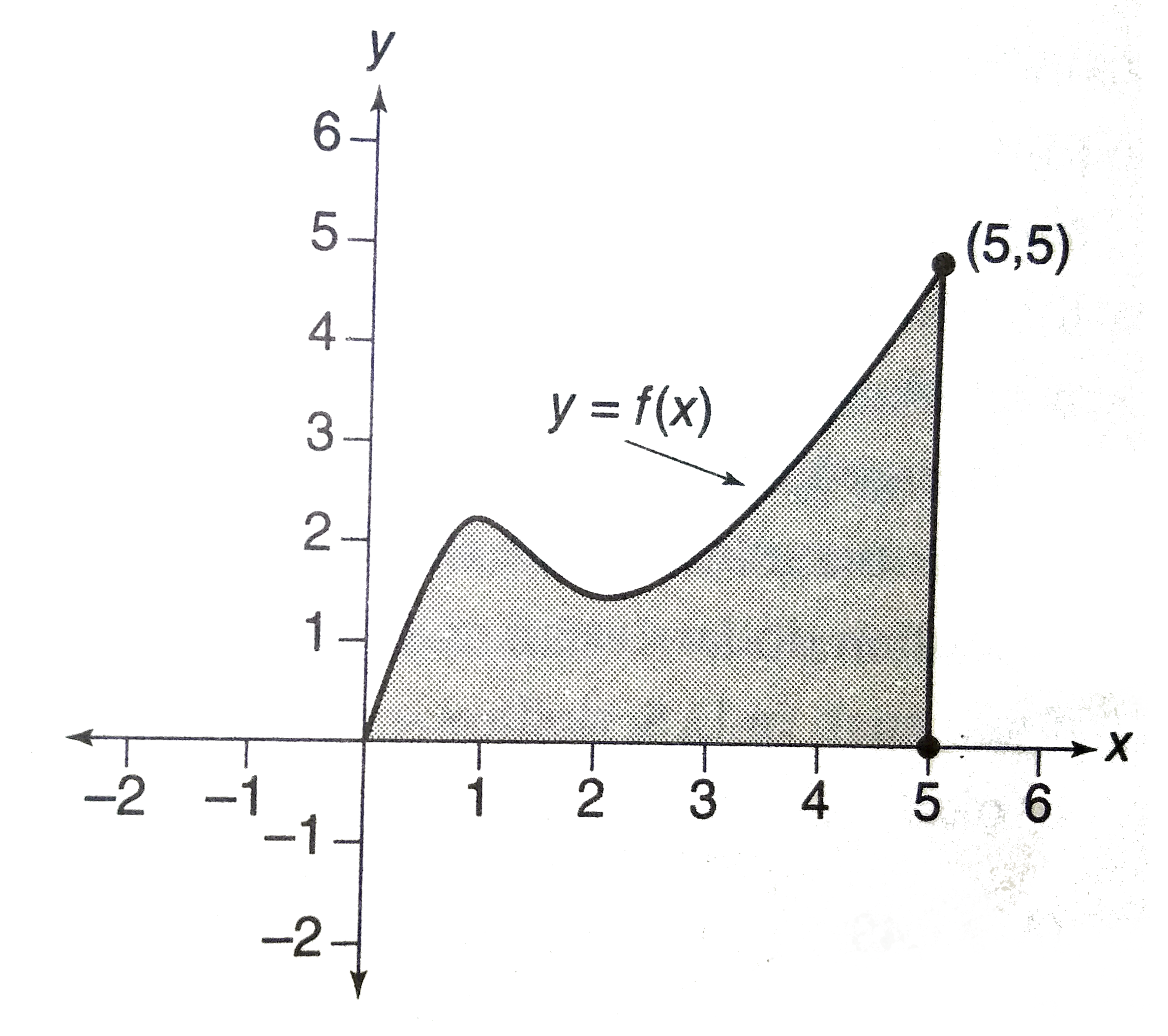
Function f is defined for 0≤x≤5, as shown in the accompanying figure. If (r, s) is a point inside the shaded region bounded by the x-axis, the line x=5 and y=f(x), which statement must be true?
I.r+s≤5
II.s≤f(r)
III.f≠s
I only
II only
III only
I and III only
The correct Answer is:B
Step by step video, text & image solution for Function f is defined for 0lexle5, as shown in the accompanying figure. If (r, s) is a point inside the shaded region bounded by the x-axis, the line x=5 and y=f(x), which statement must be true? I.r+sle5 II.slef(r) III.fnes by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A function f is defined by f(x)=2x−5. Write down the values of(i) f(0), (ii) f(7), (iii) f(3).
View Solutionf:R→R defined by f(x)=x2+5
View Solutionf:R→R given by f(x)=5-3 sin x, is
View SolutionLet f:R+→R defined as f(x)=ex+ln x and g=f−1 then correct statement (s) is/are:
View SolutionA function f:R→R is defined by f(x)=x2. Determine Range of f ii. {x:f(x)=4} iii. {y:f(y)=−1}
View SolutionLet f: R → Ris defined by/(x)= 3x + 5. Then
View SolutionLet a function f:R→R be defined as f(x)=x+sinx. The value of ∫2π0f−1(x)dx will be:
View SolutionIf a continuous function f defined on the real line R assume positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative, then the equation f(x)=0 has a root in R. Consider f(x)=kex−x, for all real x where k is a real constant.
The positive value of k for which kex−x=0 has only one root isView SolutionLet f:R→R be a function defined by f(x+1)=f(x)−5f(x)−3∀x∈R. Then which of the following statement(s) is/are true?
View SolutionThe function f:R→R is defined as f(x)=3−x. From the following statements,
I. f is one-one
II. f is onto
III. f is a decreasing function the true statements areView Solution

