A table has a heavy circular top of radius 1m and mass 20kg, placed on four light (considered massless) legs placed symmetrically on its circumference. The maximum mass that can be kept anywhere on the table without toppling it is close to
20kg
34kg
47k
59kg
The correct Answer is:C
Step by step video, text & image solution for A table has a heavy circular top of radius 1m and mass 20 kg, placed on four light (considered massless) legs placed symmetrically on its circumference. The maximum mass that can be kept anywhere on the table without toppling it is close to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
A table has a heavy circular top of radius 1 m and mass 20 kg. It has four light legs of lengths 1 m fixed symmetrically on its circumference. (a) What is the maximum mass that may be placed any where on this table without toppling the table ? (b) What is the area of the table tope over which any weight may be placed without toppling it ?
View SolutionA table has a heavy circular top of radius 1 m and mass 20 kg . It has four light legs of length 1 m fixed symmetrically on its circuference. What is the maximum weight which may be placed anywhere on this table wihtout toppling it?
View Solution
Knowledge Check
- Question 1 - Select One
Four identical rods of mass M and length L are placed on one another on the table so as to produce the maximum overhang as shown in figure. The maximum total overhang will be :
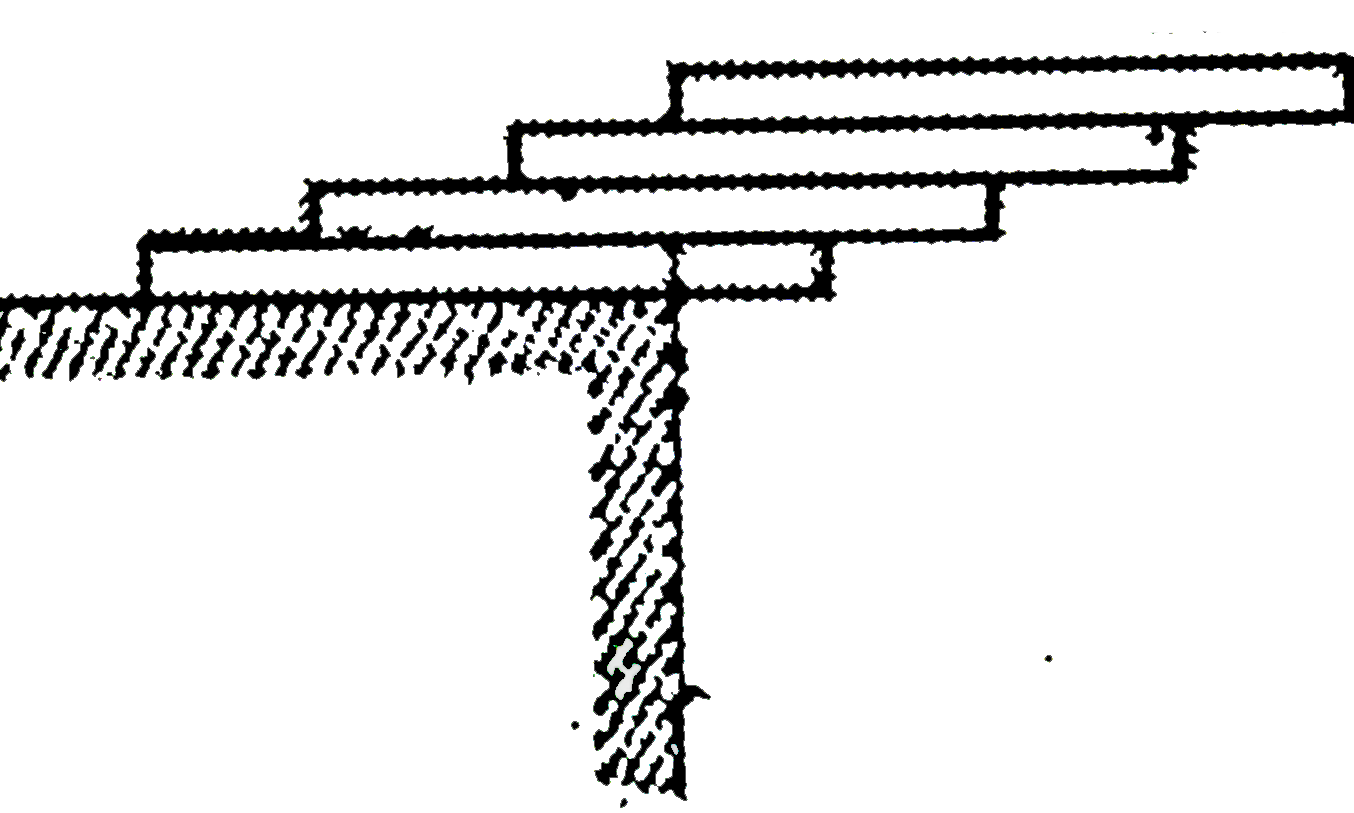 A3L4B24L25C25L24D4L3
A3L4B24L25C25L24D4L3 - Question 2 - Select One
Two identical uniform rectangular blocks (with longest side L) and a solid sphere of radius R are to be balanced at the edge of a heavy table such that the centre of the sphere remains at the maximum possible horizontal distance from the vertical edge of the table without toppling as indicated in the figure.
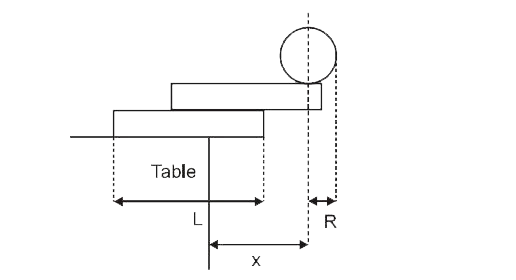
If the mass of each block is M and of the sphere is M/2, then the maximum distance x that can be achieved isA8L/15B5L/6C(3L/4 + R)D(7L/15 + R) - Question 3 - Select One
A uniform chain of length l and mass m is placed on a smooth table with one-fourth of its length hanging over the edge. The work that has to be done to pull the whole chain back onto the table is :
A14mglB18mglC116mglD132mgl
A table has a heavy circular top of radius 1m and mass 2kg. It has four light legs of length 1m fixed symmetrically on its circumference. Find the maximum mass (in kg) which may be placed anywhere on this table without toppling it. (take √2=1.4)
View SolutionA round table of radius 10 m has four vertical legs fixed at the circumference of the table top in the form of four corners of a square. If the mass of the table is 10 kg, what maximum mass (in kg) can be kept on the circumference of the table so that table doesn't topple is (x√2−y), then the value of (x+y) is ?
View SolutionTwo blocks of mass m1=10kg and m2=5kg connected to each other by a massless inextensible string of length 0.3m are placed along a diameter of the turntable. The coefficient of friction between the table and m1 is 0.5 while there is no friction between m2 and the table. the table is rotating with an angular velocity of 10rad/s. about a vertical axis passing through its center O. the masses are placed along the diameter of the table on either side of the center O such that the mass m1 is at a distance of 0.124m from O. the masses are observed to be at a rest with respect to an observed on the tuntable (g=9.8m/s2).
(a) Calculate the friction on m1
(b) What should be the minimum angular speed of the turntable so that the masses will slip from this position?
(c ) How should the masses be placed with the string remaining taut so that there is no friction on m1.View SolutionConsider three uniform solid spheres. sphere (i ) has radius r and mass m sphere (ii) has radius r and mass 3m, sphere (iii) has radius 3r and mass 'm'. All the spheres can be placed at the same point on the same inclined plane where they will roll without slipping to the bottom. If allowed to roll down the incline, then at the 'bottom of the incline
View SolutionConsider three solid spheres, sphere (i) has radius r and mass m, sphere (ii) has radius r and mass 3 m, sphere (iii) has radius 3r and mass m, All can be placed at the same point on the same inclined plane, where they will roll without slipping to the bottom, If allowed to roll down the incline, then at the bottom of the incline
View Solution

