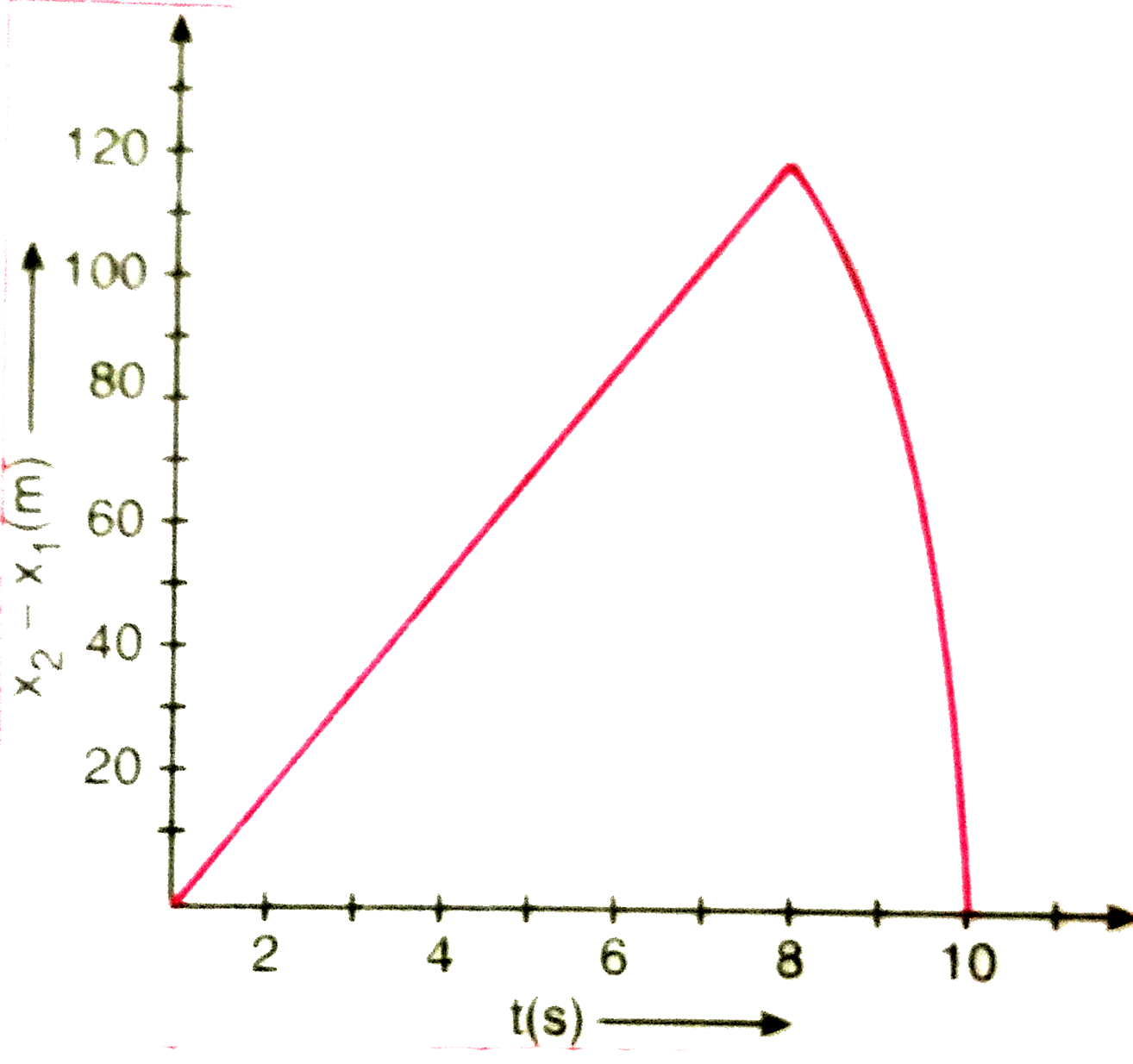
किसी 200 मीटर ऊँची खड़ी चट्टान के किनारे से दो पत्थरो को एक साथ ऊपर की ओर 15 मीटर/सेकण्ड तथा 30 मीटर/सेकण्ड की प्रारंभिक चाल से फेंका जाता है । इसका सत्यापन कीजिए कि नीचे दिखाया गया ग्राफ (चित्र 3.59) पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है वायु के प्रतिरोध को नगण्य मानिए और यह मानिए कि जमीन से टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं । मान लीजिए g=10 मीटर/सेकण्ड2 | ग्राफ के रेखीय व वक्रीय भागो के लिए समीकरण लिखिए ।
पहले पत्थर के लिए : प्रारम्भिक स्थिति (जमीन से सापेक्ष) x0=200 मीटर प्रारम्भिक वेग u1=15 मीटर/सेकण्ड तथा त्वरण a=−g=−10 मीटर/सेकण्ड2 (नीचे की ओर)
t समय बाद पहले पत्थर की स्थिति x1=x0+u1t+12at2 . . .(i)
या x1=200+15t+12(−10)t2
जब पत्थर जमीन से टकराता है x1=0
इस प्रकार 0=200+15t−5t2
या t2−3t−40=0
या (t+5)(t−8)0
या t=−5 सेकण्ड या t=8 सेकण्ड
चूँकि पत्थर को t=0 पर फेंका गया था, इस प्रकार t का ऋणात्मक मान सम्भव नहीं होगा । अतः पत्थर जमीन से 8 सेकण्ड बाद टकराता है ।
दूसरे पत्थर के लिए : प्रारम्भिक स्थिति x0=200 मीटर, प्रारम्भिक वेग u2=300 मीटर/सेकण्ड2 तथा त्वरण a=−10 मीटर/सेकण्ड2
t समय बाद इसकी स्थिति x2=x0+u2t+12at2 . . .(ii)
या x2=2000+30t+12(−10)t2 . . . (iii)
जब पत्थर जमीन से टकराता है, x2=0
इस प्रकार 0=200+30−5t2
या t2−5t−40=0
(t+4)(t−10)=0
या t=−4 सेकण्ड या t=10 सेकण्ड
t का ऋणात्मक मान इस स्थिति में भी संभव नहीं है अतः दूसरा पत्थर जमीन से 10 सेकण्ड बाद टकराता है |
8 सेकण्ड तक, पहले के सापेक्ष दूसरे पत्थर की तुलनात्मक स्थिति का मान समीकरण (i) व (ii) से, x2−x1=(u2−u1)t
=(30−15)t
या x2−x1=15t (iv)
समीकरण (iv) दोनों पत्थरो का रैखिक पथ दर्शाता है, (x2−x1) तथा t1 बीच रैखिक समीकरण के कारण, ग्राफ (चित्र 3.59) में 8 सेकण्ड तक वक्र सरल रेखा होती है ।
t=8 सेकण्ड में दोनों पत्थरो के बीच अधिकतम दूरी,
(x2−x1)अधिकतम=15×8=120 मीटर (ग्राफ से)
सेकण्ड बाद, सिर्फ दूसरा पत्थर ही गतिमान होगा जब तक कि वह t=10 सेकण्ड पर जमीन से टकराता है इस प्रकार समीकरण (iii) से 8 सेकण्ड तथा 10 सेकण्ड के बीच की गति अर्थात x2=200+30t−5t2 होगी ।
यह एक द्विघात समीकरण है अतः यह ग्राफ के वक्र भाग को दर्शाती है | t=10 सेकण्ड बाद दोनों पत्थर की स्थिति जमीन पर होगी तथा दोनों के बीच दूरी शून्य होगी ।
Topper's Solved these Questions
- सरल रेखा में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - अतिरिक्त महत्वपूर्ण स्मरणीय तथ्य
8 Videos
- सरल रेखा में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - बोधात्मक प्रश्न
8 Videos
- सरल रेखा में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - संख्यात्मक प्रश्न (गति के समीकरण)
21 Videos
- समतल में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - समतल में गति EXERCISE - वस्तुनिष्ठ प्रश्न
58 Videos
- सरल रेखा में गति एवं समतल में गति BOOK - SHIVLAAL PUBLICATIONCHAPTER - सरल रेखा में गति एवं समतल में गति EXERCISE - एक शब्द/ वाक्य में उत्तर
8 Videos
Similar Questions
यदि कोई वस्तु कुल चली गयी दूरी की आधी दूरी v1 वेग से तथा शेष आधी दूरी वेग v2 से तय करती है तो गति दौरान वस्तु का वेग निम्न होगा :
vav=(S/2)+(S/2)(S/2v1)+(S/2v1)=2v1v2v1+v2
View Solutionक्या यह सम्भव है कि
किसी वस्तु का वेग नियत हो, लेकिन चाल परिवर्ती हो ?
View Solutionएक बस वेग 30 किमी/घण्टा से चल रही है ब्रेक लगाने पर वह 10 मीटर चलकर रूक जाती है । बस के रूकने में लगे समय की गणना कीजिए ।
View Solutionनिम्नलिखित में से अदिश राशि है :
View Solutionθ कोण पर झुके हुए दो सदिश →A व →B के परिणामी सदिश के परिणाम के लिए सूत्र लिखिए|
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक 13 मीटर लम्बी सीढ़ी दीवार के सहारे झुकी हुई है। सीढ़ी के पाद को 1.5 मी./से. की दर से जमीन के सारे दीवार से दूर खींचा जाता है। सीढ़ी तथा जमीन के मध्य का कोण किस गति से परिवर्तित हो रहा है जबकि सीढ़ का पावि दीवार से 12 मीटर दूर हो ।
View Solutionग्राफ की सहायता से गति के समीकरणों को व्युत्पन्न करना
View Solutionअंकित पूर्व दिशा की ओर चलना शुरू करता है | 30 मीटर चलने के बाद वह बाएं मुड़ जाता है और 40 मीटर चलता है फिर वह बाएं मुड़ जाता है और 30 मीटर दूर चलता है | अब वह पुनः बाएं मुड़ता है और 50 मीटर चलता है | तब वह अपनी प्रारम्भिक स्थिति से कितनी दूर है ?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionजब दो तत्वों A और D के दो यौगिकों ACl_(3) और DCl_(3) को एक साथ मिश्रित किया जाता है, तो एक यौगिक ADCl_(6) का निर्माण होता है। संरचनात्मक विश्लेषण से पता चला कि ADCl_(6) एक आयनिक यौगिक है। दिया गया है कि DCl_(3) त्रिकोणीय समतल है और ACl_(3) त्रिकोणीय पिरामिडीय है, ऋणायन DCl_(4)^(-) की आकृति ज्ञात कीजिए।
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionग्लूकोज के ताजा तैयार विलयन से समय के साथ प्रकाशिक घूर्णन में परिवर्तन को निम्न में जाना जाता है -
View Solutionएक गैस को इस तरह गर्म किया जाता है कि उसका दाब और आयतन दोनों दोगुने हो जाते हैं। तब ताप में कमी करके वायु के कुछ अणुओं को पात्र में मिलाया जाता है ताकि दोगुने किये गए आयतन और दाब को बनाये रखा जा सके। माना कि प्रारंभिक मोलों की संख्या के 1वें भाग को इस उद्देश्य के लिए मिलाया गया है। तब प्रारंभिक परमताप के सापेक्ष परिणामी ताप का प्रभाज क्या होगा?
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solution
