A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass ?Solution in Tamil
Step by step video & image solution for A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed it completely. Calculate the raise of the water in the glass ? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBOOK - SURA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Exercise 7.3
8 Videos
- MENSURATIONBOOK - SURA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Exercise 7.4
8 Videos
- MENSURATIONBOOK - SURA PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Unit Test (Section -C)
2 Videos
- GOVT. MODEL QUESTION PAPER-2019-20BOOK - SURA PUBLICATIONCHAPTER - GOVT. MODEL QUESTION PAPER-2019-20EXERCISE - Part-IV
6 Videos
- NUMBER AND SEQUENCESBOOK - SURA PUBLICATIONCHAPTER - NUMBER AND SEQUENCESEXERCISE - Unit test
12 Videos
Similar Questions
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel.
View SolutionAn aluminium sphere of radius 12 cm is melted to make a cylinder of radius 8 cm. Find the height of the cylinder.
View SolutionA shuttle cock used for playing badminton has the shape of a frustum of a cone is mounted on a hemisphere. The diameters of the frustum are 5 cm and 2 cm. The height of the entire shuttle cock is 7 cm. Find its external surface area.
View SolutionFind two consecutive positive integers, sum of whose squares is 365.
View SolutionUsing Euclid's division lemma, if the cube of any positive integers is divided by 9 then the possible remainders are ___.
View SolutionA glass cylinder with diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which water will rise in the cylinder. (Take π=3.142)
View Solutionएक गोला जिसका व्यास 12 सेमी है, एक लम्बवृतिये बर्तन में डाला जाता है जिसमे थोड़ा बेलनाकार बर्तन में पानी में पूरा डूब जाता है तो बेलनाकार बर्तन में पानी की सतह 359 सेमी बढ़ जाती है, तो बेलनाकार बर्तन का व्यास ज्ञात कीजिए ।
View Solutionएक शंक्वाकार बर्तन जिसके आधार की त्रिज्या 5 सेमी और ऊंचाई 24 सेमी है, पानी से पूरा भरा है । इस पानी को एक बेलनाकार बर्तन में पलटा जाता है जिसके आधार की त्रिज्या 10 सेमी है । बेलनाकार बर्तन में पानी ऊंचाई ज्ञात कीजिए| (π=227) (अथवा) एक शंक्वाकार बर्तन, जिसका आन्तरिक व्यास 10 सेमी है और ऊंचाई 24 सेमी है, पानी से भरा है। पानी को एक बेलनाकार पात्र, जिसकी आन्तरिक व्यास 20 सेमी है, में डाला जाता है । बेलनाकार पात्र में डेल गए पानी की ऊंचाई ज्ञात कीजिए ।
View Solution5 सेमी त्रिज्या तथा 24 सेमी ऊँचाई के एक शंक्वाकार बर्तन का 34 भाग पानी से भरा है । इस पानी को एक बेलनाकार बर्तन जिसकी आन्तरिक त्रिज्या 10 सेमी है, में खाली किया जाता है । बेलनाकार बर्तन में पानी की ऊँचाई ज्ञात कीजिए ।
View Solutionएक 6 सेमी. त्रिज्या वाले गोले को आंशिक रूप से भरे पानी के बेलनाकार बर्तन में डाला जाता है। बतेन की त्रिज्या 8 सेमी. है। यदि गोला इसमें पूणत: डूब जाता हो, तो ऊपर उठे पानी को ऊँचाई है:
View SolutionAs shown in the figure, a cylindrical glass contains water with a metallic sphere of diameter 2 cm immersed in it. Find the volume of the water.
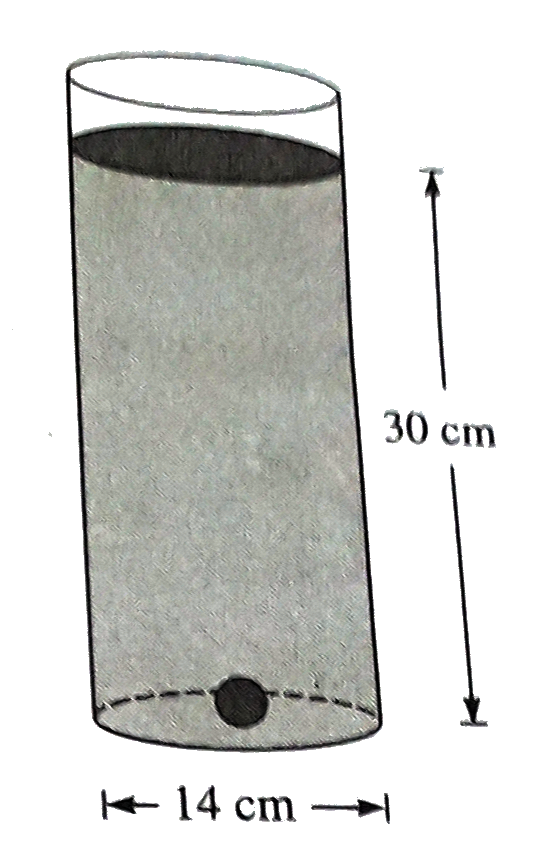
View Solutionएक बेलनाकार बर्तन, जिसके आधार की त्रिज्या 7.5 सेमी है, में कुछ पानी भरा है, 4 सेमी त्रिज्या का बेलन पूरा डूबा देने पर पानी का तल 5 सेमी ऊँचा उठ जाता है। डुबाये गये बेलन की ऊँचाई ज्ञात कीजिए।
View SolutionAs shown in the figure, a cylindrical glass contains water. A metal sphere of diameter 2 cm is immersed in it. Find the volume of the water.
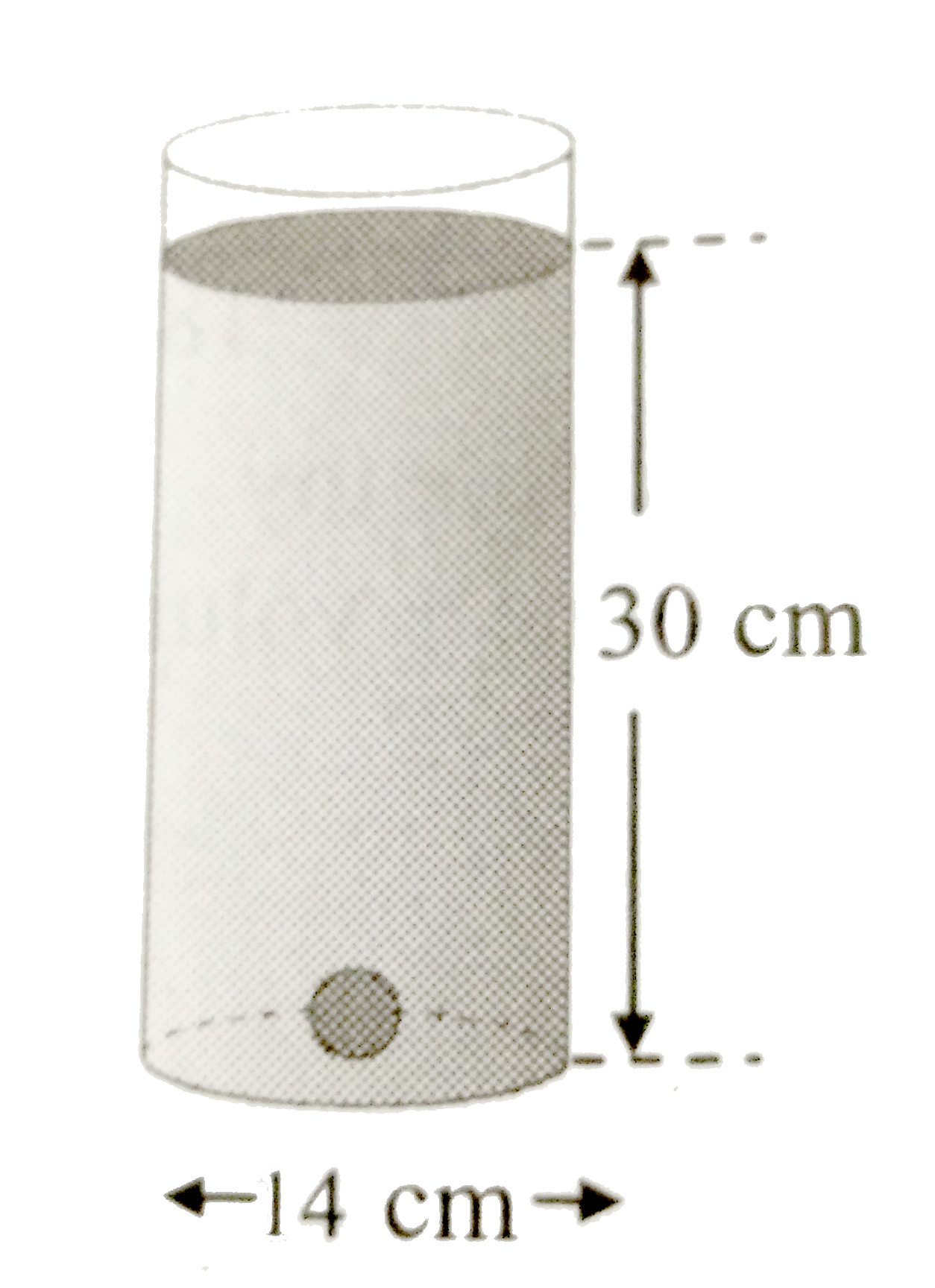
View SolutionA glass cylinder with diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which water will rise in the cylinder. (Take π=3.142)
View SolutionA glass cylinder with diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which water will rise in the cylinder. (Take π=3.142)
View Solution
