Suppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function
Find
the distribution functionSolution in Tamil
Step by step video & image solution for Suppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function f(x)={{:(k, 200 le x le 600), (0, "otherwise"):} Find the distribution function by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONSBOOK - SURA PUBLICATIONCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.4
11 Videos
- PROBABILITY DISTRIBUTIONSBOOK - SURA PUBLICATIONCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.5
13 Videos
- PROBABILITY DISTRIBUTIONSBOOK - SURA PUBLICATIONCHAPTER - PROBABILITY DISTRIBUTIONSEXERCISE - EXERCISE 11.2
9 Videos
- ORDINARY DIFFERENTIAL EQUATIONSBOOK - SURA PUBLICATIONCHAPTER - ORDINARY DIFFERENTIAL EQUATIONSEXERCISE - ADDITIONAL QUESTIONS
24 Videos
- THEORY OF EQUATIONSBOOK - SURA PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - 4 MARKS
5 Videos
Similar Questions
For the random variable X with the given probability mass function as below, find the mean and variance.
f(x)=⎧⎨⎩110x=2,515x=0,1,3,4
View SolutionCompute P(X=k) for the binominal distribution, B(n,p) where
n=6,p=13,k=3
View SolutionThree fair coins are tossed simultaneously. Find the probability mass function for number of heads occurred.
View SolutionThe order and degree of the differential equation [(d2ydx2)+(dydx)2]12=d3ydx3 are
View SolutionIf the sum of the roots of the quadratic equation ax2+bx+c=0 ( abc ≠ 0) is equal to the sum of the squares of their reciprocals, the sum of the squares of their reciprocals, then ac,ba,cb are in H.P.
View SolutionFollowing is the distribution function F(x) of a X.

Find P(X≤3),P(2≤X≤5)
View SolutionShow that the function f(x) defined by .f(x)=17, for 1≤x≤8 =0, otherwise, is a probability density function for a random variable. Hence find P(3<X<10)
View SolutionProbability distribution of X is given by
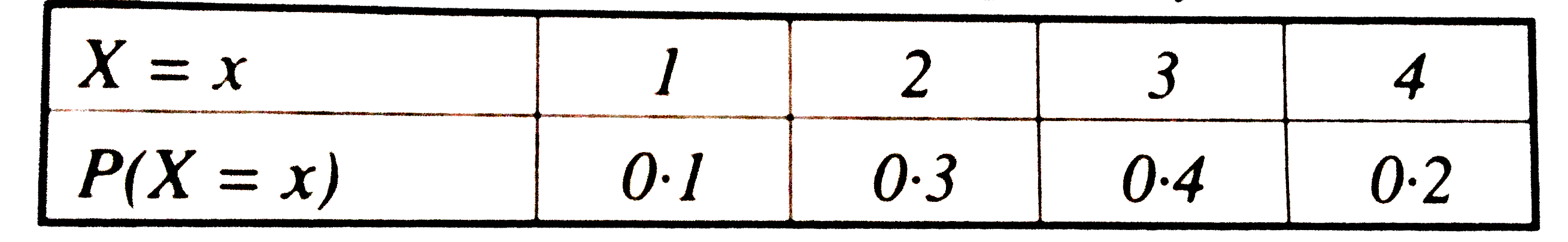
Find P(X≤2) and obtain cumulative distribution function of X.
View SolutionThe probability density function of X is given by f(x)={kxe−2xfor x>00for x≤0 Find the value of k.
View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(0.2≤X<0.6)
View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(1.2≤X<1.8)
View SolutionThe probability density function of X is
f(x)=⎧⎪⎨⎪⎩x0<x<12−x1≤x<20otherwise
Find
P(0.5≤X<1.5)
View SolutionSuppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function
f(x)={k200≤x≤6000otherwise
Find
the value of k
View SolutionSuppose the amount of milk sold daily at a milk booth is distributed with a minimum of 200 litres and a maximum of 600 litres with probability density function
f(x)={k200≤x≤6000otherwise
Find
the probability that daily sales will fall between 300 litres and 500 litres?
View SolutionThe probability density function of X is given by f(x)={ke−x3for x>00for x≤0
Find
the value of k
View Solution
