In Fig 3E.17, the mass rests on a rough table. The mass is pushed against the spring to which it is not attached Force constant of the spring is k, coefficient of friction is .
(a) Find the speed of the blocks after the spring is released and has fallen a distance of .
(b) If the spring is attached to the block and it falls a distance before coming to rest, calculate the coefficient of friction .
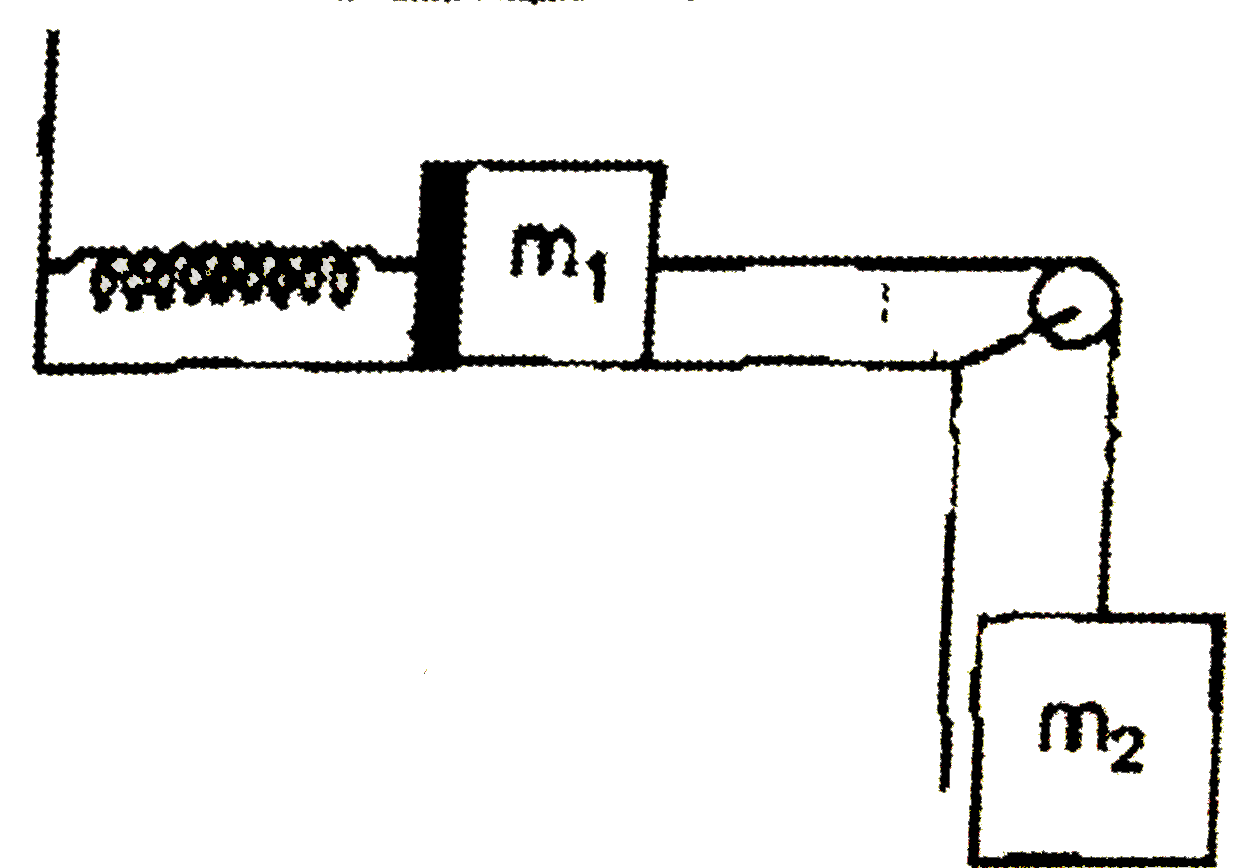
Step by step video & image solution for In Fig 3E.17, the mass m_(2) rests on a rough table. The mass m_(1) is pushed against the spring to which it is not attached Force constant of the spring is k, coefficient of friction is mu_(k). (a) Find the speed of the blocks after the spring is released and m_(2) has fallen a distance of h. (b) If the spring is attached to the block and it falls a distance h before coming to rest, calculate the coefficient of friction mu_(k). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 153videos
WORK AND ENERGY
- BOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 218videos
WORK AND ENERGY
- BOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Matching types problems14videos
WORK AND ENERGY
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.
 View Solution
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A mass m is attached to a spring. The spring is stretched to x by a force F and refeased. After being released, the mass comes to rest at the initial equilibrium position. The coeffiecient of friction, μk , is :−
 Aμk=2KxmgBμk=2mgFCμk=F2mgDμk=mg2Kx
Aμk=2KxmgBμk=2mgFCμk=F2mgDμk=mg2Kx - Question 2 - Select One
In the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
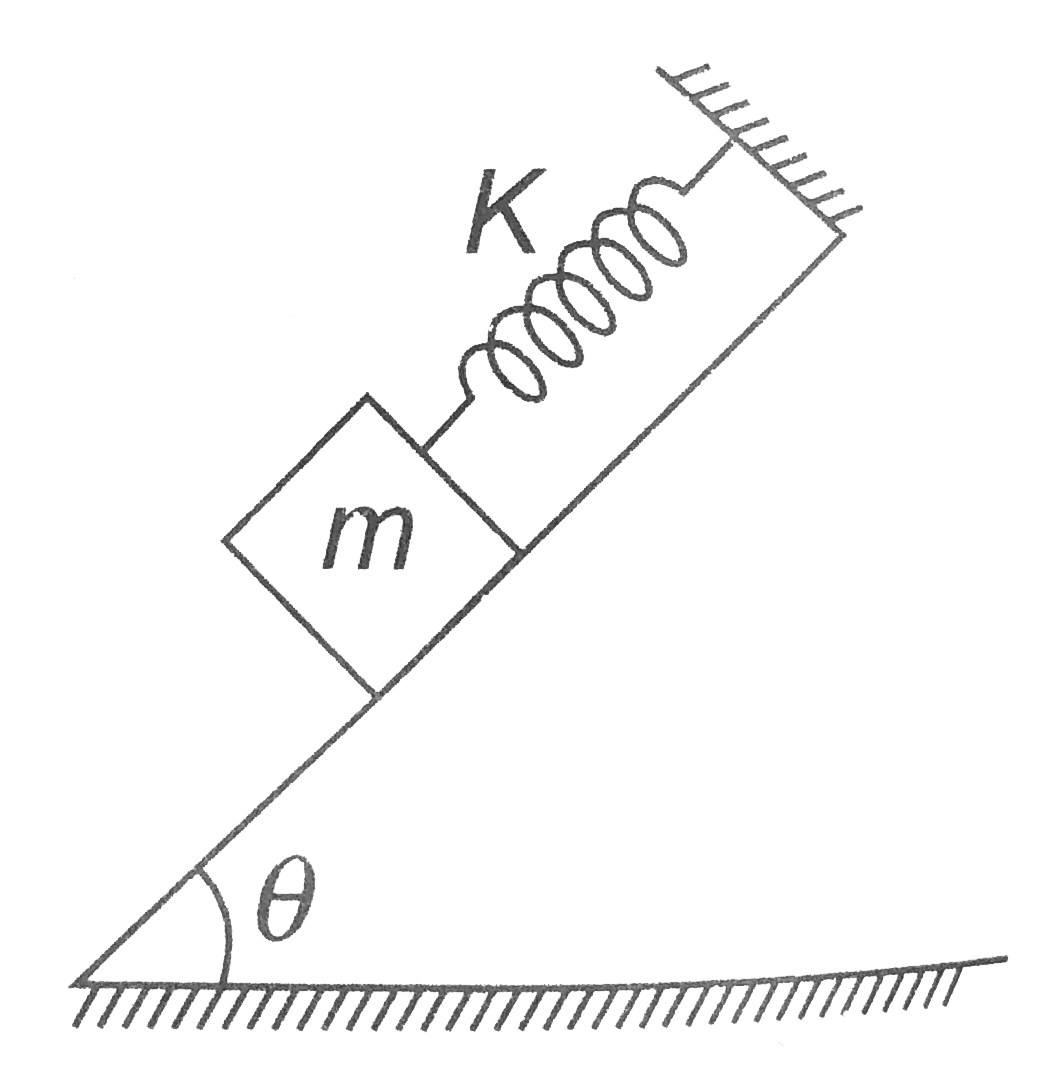 A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mk
A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mk - Question 3 - Select One
A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
Force constant of a spring is 100 N/m. If a 10kg block attached with the spring is at rest, then find extension in the spring.
(g=10m/s2)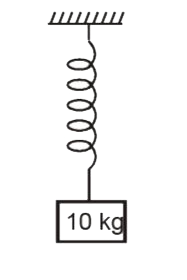 View Solution
View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionTwo blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
View SolutionA block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=34. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)
 View Solution
View SolutionIn the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.
 View Solution
View Solution

