A particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form U(x)=ax2−bx where a and b are positive constants. The position of equilibrium is:
b2a
2ba
ab
2ab
The correct Answer is:D
Topper's Solved these Questions
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 2
18 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Level 3
34 Videos
- WORK AND ENERGYBOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Eample
47 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions
The potential energy U in joule of a particle of mass 1kg moving in x−y plane obeys the lawU=3x+4y, where (x,y) are the co-ordinates of the particle in metre. If the particle is at rest at (6,4) at time t=0 then :
View SolutionIn the shown figure, the spring and string is ideal. The spring the stiffness of 100N/m and m=1kg friction exists between mass 2m and surface with coefficient μ=0.8. The system is released with spring from its relaxed position. Based on above data, answer the following question: (take g=10m/s2)
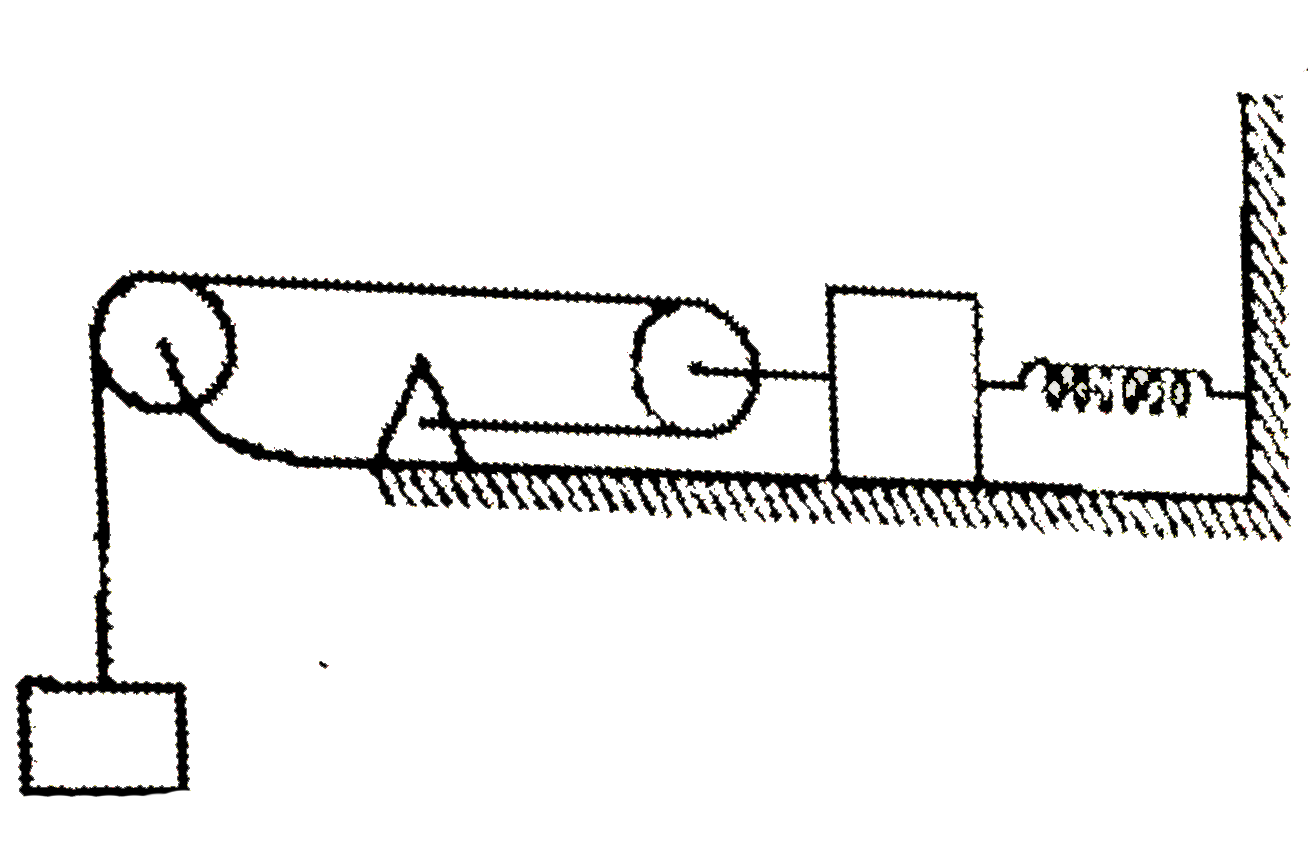
Maximum extension in spring is :
View SolutionAn object is displaced from position vector →r1=(2ˆi+3ˆj)m to →r2==(4ˆj+6ˆk)m under a force →F=(3x2ˆi+2yˆj)N. Find the. work done this force.
View SolutionMatch the column :
Column-I (Quantity)Column-II(Unit)(a)Energy density (Energy per unit volume)(p)dyne/cm2(b)Force constant of a spring(r)kg−m/s(c)Pressure(r)erg/cm2(s)pascal
View SolutionA particle located in a one-dimensional potential field has its potential energy function as U(x)=ax4−bx2, where a and b are positive constants. The position of equilibrium x corresponds to
View SolutionA particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=ax2−bx, where a and b are positive constant. The particle will perform.
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=-ax^2+bx^4 , where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form u(x) = a/x^(2)-b/x) , where a and b are positive constants. Find the period of small oscillations of the particle.
View SolutionA particle located in one dimensional potential field has potential energy function U(x)=(a)/(x^(2))-(b)/(x^(3)) , where a and b are positive constants. The position of equilibrium corresponds to x equal to
View SolutionThe potential energy of a particle in a certain field has the form U=a/r2−b/r, where a and b are positive constants, r is the distance from the centre of the field. Find:
(a) the value of r0 corresponding to the equilibrium position of the particle, examine where this position is steady,
(b) the maximum magnitude of the attraction force, draw the plots U(r) and Fr(r) (the projections of the force on the radius vector r).
View SolutionA particle of mass m is located in a one dimensional potential field where potential energy is given by
V(x) = A(1- cos Px) , where A and P are constant . The period of small oscillations of the particle is
View SolutionA particle located in a one-dimensional potential field has its potential energy function as U(x)(a)/(x^4)-(b)/(x^2) , where a and b are positive constants. The position of equilibrium x corresponds to
View SolutionA particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=ax2−bx, where a and b are positive constant. The particle will perform.
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=−ax2+bx4, where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA particle located in one dimensional potential field has potential energy function U(x)=(a)/(x^(2))-(b)/(x^(3)) , where a and b are positive constants. The position of equilibrium corresponds to x equal to
View Solution
