A block speed of mass m and a pan of equal mass are connected by a string going over a smooth light pulley. Initially, the system is at rest, then a particle of mass m falls on the pan ad sticks to it. If the particle strikes the pan with a speed v, find the speed with which the system moves just after the collision.
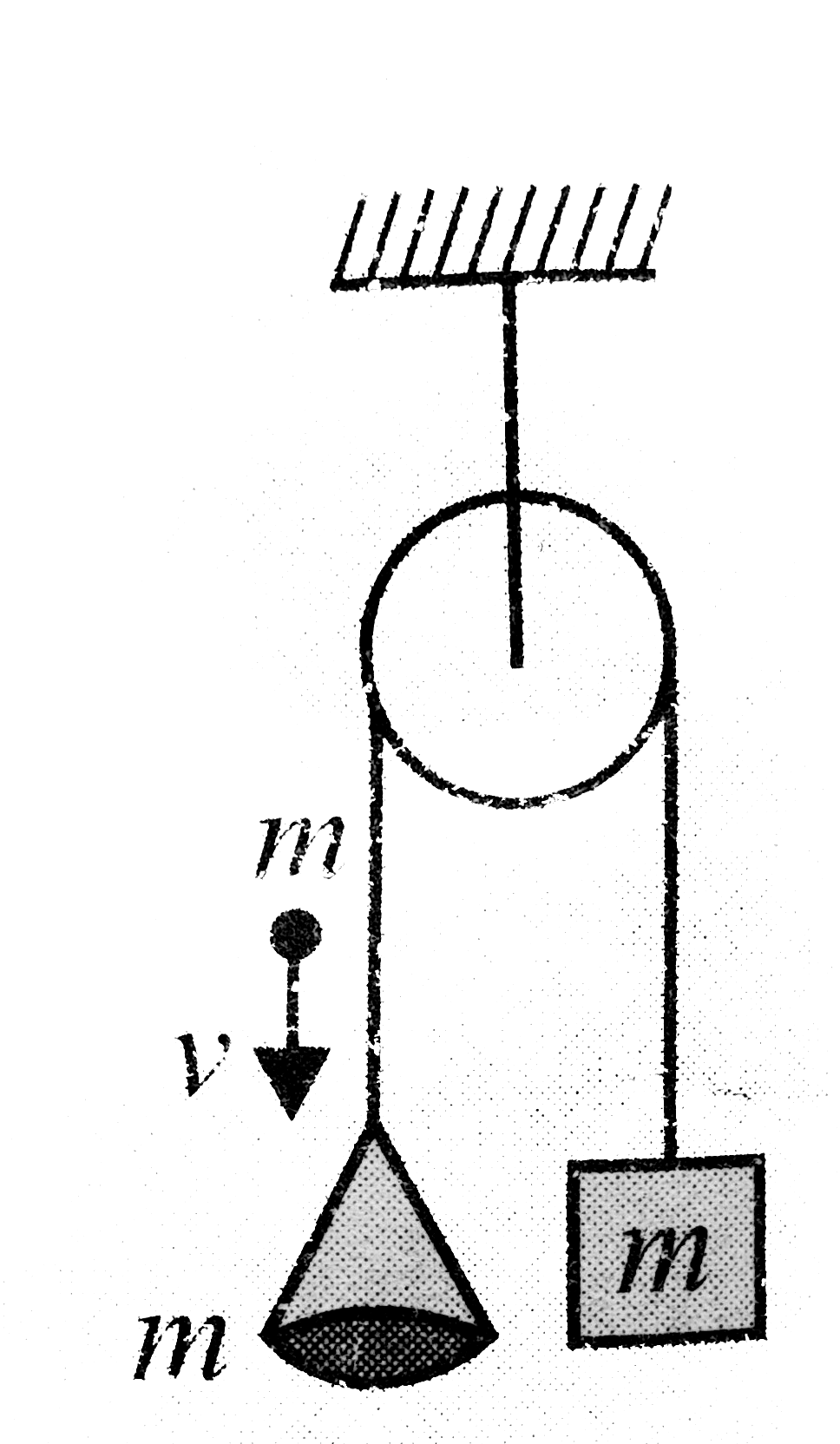
Step by step video & image solution for A block speed of mass m and a pan of equal mass are connected by a string going over a smooth light pulley. Initially, the system is at rest, then a particle of mass m falls on the pan ad sticks to it. If the particle strikes the pan with a speed v, find the speed with which the system moves just after the collision. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Example50videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Level 1110videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
Similar Questions
A block of mass m and α pan of equla mass are connected by a string going over a smooth light pulley as shwon in figure. Initially the systemis at rest when a particle of mass m falls on the pan and sticks to it. If the particle strikes thepan witha speed v find the speed with which the system moves just after the collision.
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it. The speed of the system will be
View Solution
Knowledge Check
- Question 1 - Select One
Two masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
Ag(M−mM+m) downwardBg(M−mM+m)2 downwardCg(M−mM+m)2 upward if M<mDzero - Question 2 - Select One
Two bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
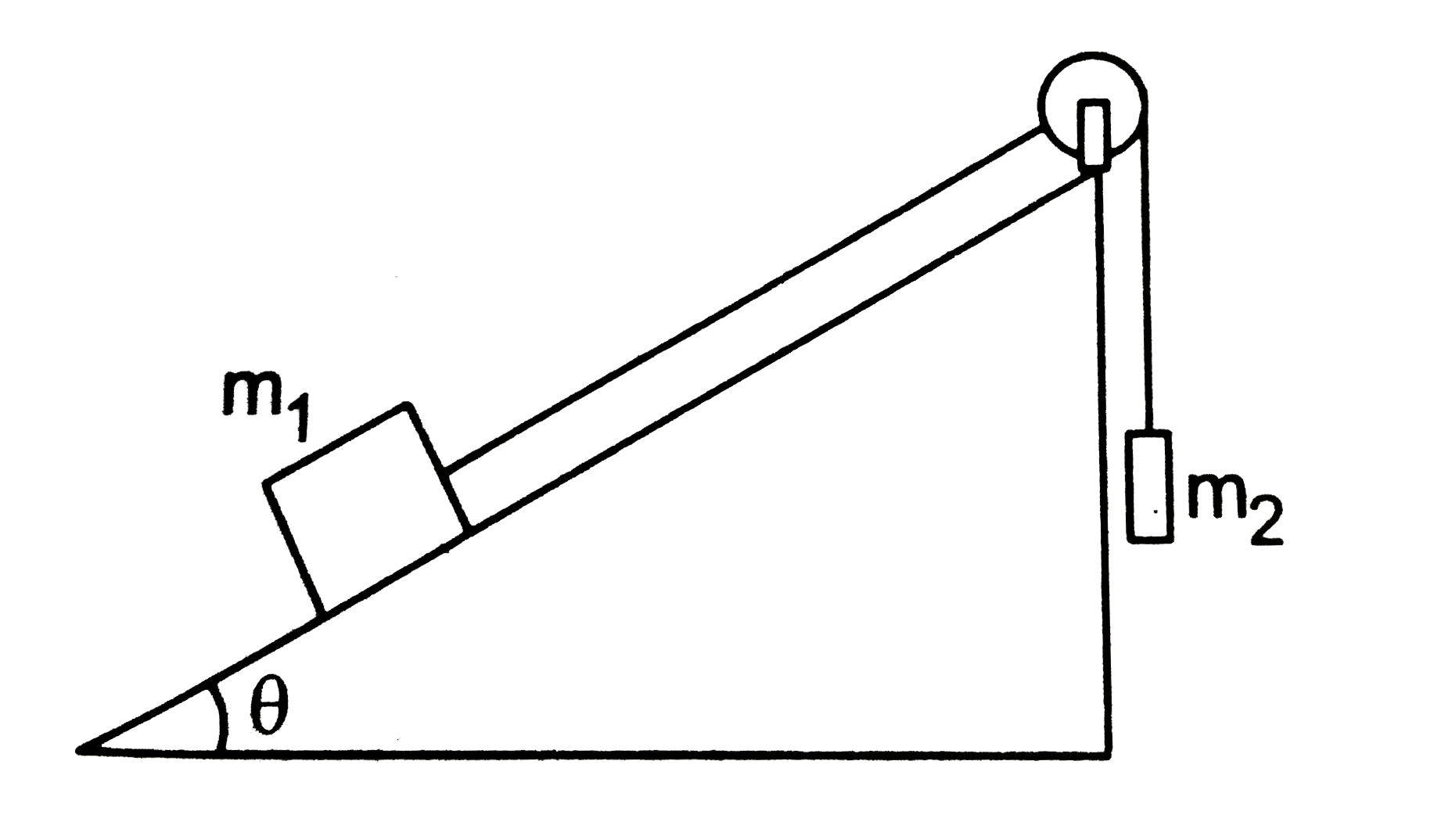Asinθ=2m2m1 , N=m1gcosθBsinθ=m2m1 , N=m1gcosθCsinθ=m2m1 , N=m1gsinθDsinθ=m2m1 , N=4m1gcosθ - Question 3 - Select One
A particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
A0.8vB0.2vC0.6vD0.4v
A particle of mass m moving with velocity v strikes a stationary particle of mass 2m and sticks to it. The speed of the system will be.
View SolutionA particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
View SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.
Find the velocity of pan + ball system at t=2.6s. Assume that the block comes to rest instantaneously after striking the floor.View SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.
Find the time t at which the block strikes the floor for the first timeView SolutionA pan of mass m=1.5kg and a block of mass M=3kg are connected to each other by a light inextensible string, passing over a light pulley as shown in Fig. Initially, the block is resting on a horizontal floor. A ball of mass m0=0.5kg collides with the pan at a speed v0=20m/s. Consider this instant of collision as t=0. Assume collision to be perfectly inelastic. Now, Fig. answer the following questions based on the above information.
. Find the maximum height reached by the block alter the second jerk.View Solution