A man hangs from a rope attached to a hot-air balloon. The mass of the man is greater than the mass of the balloon and its constents. The system is stationary in air. If the man now clims up to the balloon using the rope, the centre of mass of the man plus balloon system will
remain stationary
move up
move down
first move up and then return to its intial position
The correct Answer is:a
Step by step video, text & image solution for A man hangs from a rope attached to a hot-air balloon. The mass of the man is greater than the mass of the balloon and its constents. The system is stationary in air. If the man now clims up to the balloon using the rope, the centre of mass of the man plus balloon system will by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A person of mass m is hanging from a rope fastened to a stationary balloon of mass M If the person climbs the rope , then with what velocity the balloon would move and in what direction ?
View SolutionA man of mass m is suspended in air by holding the rope of a ballon of mass M. As the man climbs up the rope, the ballon

View Solution
Knowledge Check
A ladder of length l carrying a man of mass m at its end is attached to the basket of a balloon of mass M. The entire system is in equilibrium in the air. As the man climbs up the ladder into the balloon, the balloon descends by a height h.
The work done by the man isA(a) mglB(b) mghC(c) mgD(d) mg(l−h)A ladder of length l carrying a man of mass m at its end is attached to the basket of a balloon of mass M. The entire system is in equilibrium in the air. As the man climbs up the ladder into the balloon, the balloon descends by a height h.
The potential energy of the balloonA(a) Decreases by mghB(b) Increases by mghC(c) Increases by mgl(l−h)D(d) Increases by mglA rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
AmMvrBm2MvrCMmvrD2Mmvr
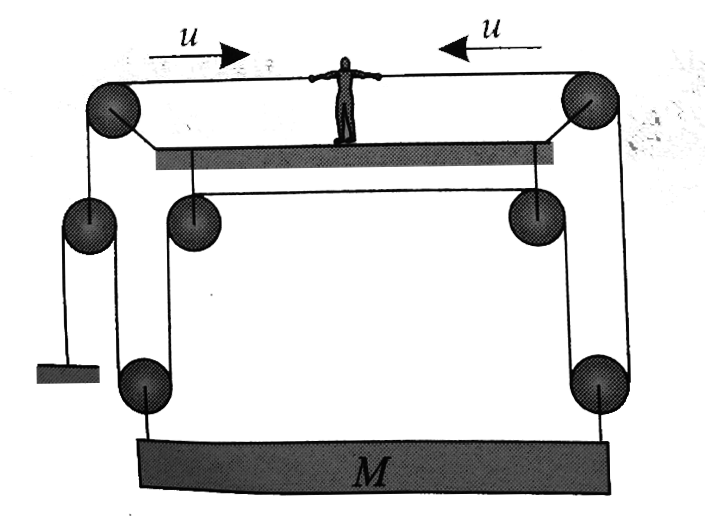
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.
View SolutionA man of mass M hanging with a light rope which is connected with a balloon of mass m. the system is at rest in air. When man rises a distance h with respect to balloon find. The distance raised by man
View SolutionA ladder of length l carrying a man of mass m at its end is attached to the basket of a balloon of mass M. The entire system is in equilibrium in the air. As the man climbs up the ladder into the balloon, the balloon descends by a height h.
The potential energy of the man
View SolutionA balloon of mass M with a light rope having monkey on the rope is in equilibrium. If the monkey starts moving up with acceleration a w.r.t. rope . Then the acceleration of cenre of mass of the system is

View SolutionTwo similar balloons filled with helium gas are tied to Lm long string. A body of mass m is tied to another ends of the strings. The balloons float on air at distance r. If the amount of charge on the ballons is same then the magnitude of charge on each balloon will be
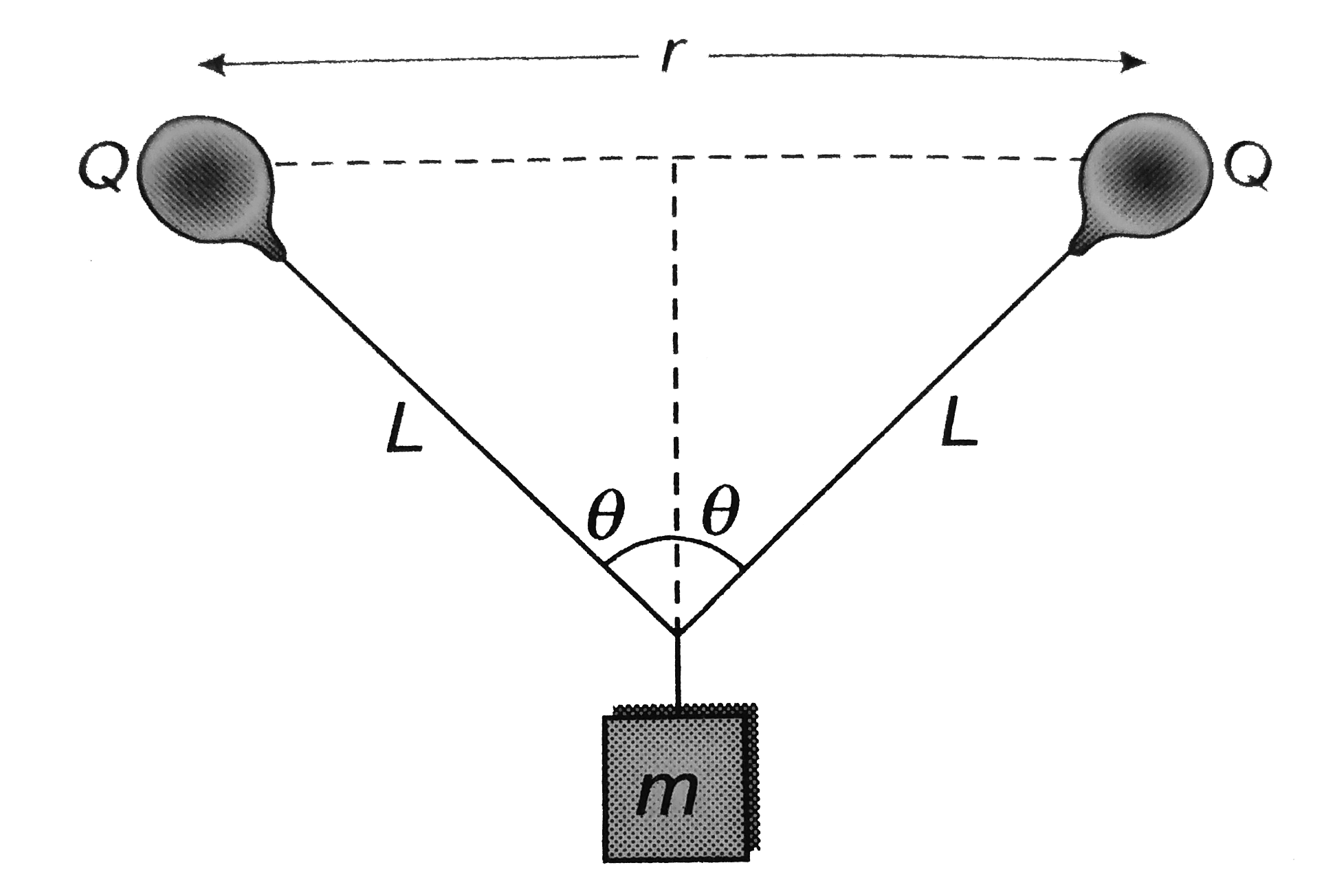
View Solution
