A stationary swimmer S, inside a liquid of refractive index μ1, is at a distance d from a fixed point P inside the liquid. A rectangular block of width t and refractive index μ2(μ2<μ1) is now placed between S and P.S will observer P to be at a distance
d−t(μ1μ2−1)
d−t(1−μ2μ1)
d+t(1−μ2μ1)
d+t(μ1μ2−1)
The correct Answer is:D
Step by step video, text & image solution for A stationary swimmer S, inside a liquid of refractive index mu_(1), is at a distance d from a fixed point P inside the liquid. A rectangular block of width t and refractive index mu_(2)(mu_(2) lt mu_(1)) is now placed between S and P.S will observer P to be at a distance by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An equiconvex lens of refractive index μ2 is placed such that the refractive :
View SolutionTwo parallel rays are travelling in a medium of refractive index μ1=43 . One of the rays passes through a parallel glass slab of thickness t and refractive index μ2=32 The path difference between the two rays due to the glass slab will be
View Solution
Knowledge Check
A prism of refractive index μg deviates the incident ray towards its base. If it is immersed in a transparent liquid of refractive index μ1 such that μ1>μg then prism would
Adeviate the ray towards its baseBdeviate the ray away from its baseCbot deviate the ray at allDnothing can be saidA convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
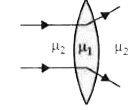 Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
A ray of light ab passing through air enters a liquid of refractive index μ1 at the boundary XY. In the liquid, the ray is shown as bc. The angle between ab and bc ( angle of deviation) is δ. The ray then passes through a rectangular salb ABCD of refractive index μ2(μ2>μ1) and emerges from the slab as the ray de. The angle between XY and AB is θ. The angle between ab and de isAδBδ+θCδ+sin−1(μ1μ2)Dδ+θ−sin−1(μ1μ2)
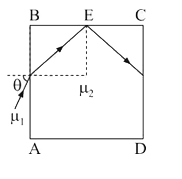
A transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:
View SolutionTwo parallel rays are travelling in a medium of refractive index μ1=4/3. One of the rays passes through a parallel glass slab of thickness t and refractive index μ2=3/2. The path difference between the two rays due to the glass slab will be
View SolutionIf refractive index of core & cladding are μ1 & μ2 respectively then :
View SolutionIf refractive index of core & cladding are μ1&μ2 respectively then :
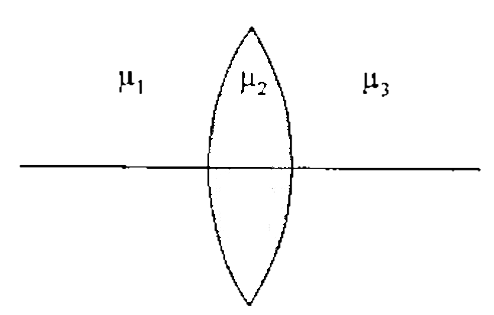
View SolutionA double convex lens, lens made of a material of refractive index μ1, is placed inside two liquids or refractive indices μ2 and μ3, as shown. μ2>μ1>μ3. A wide, parallel beam of light is incident on the lens from the left. The lens will give rise to

View Solution
