With t taken in seconds and I taken in amp, the variation of I follows the equation t2+I2=25
What amount of Ag will be electrodeposited with this current flowing in the interval 0-5 second? (Ag=108)
22 mg
66 mg
77 mg
88 mg
The correct Answer is:A
To solve the problem, we need to find the amount of silver (Ag) that will be deposited when a current varies according to the equation t2+I2=25 over the interval from 0 to 5 seconds.
1. Understand the Equation:
The equation t2+I2=25 describes a relationship between time t and current I. We can rearrange this to express I in terms of t:
I=√25−t2
2. Determine the Current Over Time:
We need to calculate the total charge Q that flows through the circuit from t=0 to t=5 seconds. The charge can be calculated using the formula:
Q=∫50I(t)dt=∫50√25−t2dt
3. Evaluate the Integral:
The integral ∫√25−t2dt can be solved using trigonometric substitution. Let t=5sin(θ), then dt=5cos(θ)dθ. The limits change from t=0 to t=5 which corresponds to θ=0 to θ=π2.
Q=∫π20√25−(5sin(θ))2⋅5cos(θ)dθ
Simplifying inside the square root:
Q=∫π20√25(1−sin2(θ))⋅5cos(θ)dθ=∫π205⋅5cos2(θ)dθ=25∫π20cos2(θ)dθ
4. Use the Integral of Cosine Squared:
The integral ∫cos2(θ)dθ can be evaluated using the identity:
∫cos2(θ)dθ=12(θ+12sin(2θ))
Evaluating from 0 to π2:
∫π20cos2(θ)dθ=π4
Therefore,
Q=25⋅π4=25π4
5. Calculate the Amount of Silver Deposited:
According to Faraday's law, the amount of substance deposited is given by:
m=Q⋅MF
where M is the molar mass of silver (Ag = 108 g/mol) and F is Faraday's constant (F=96500C/mol):
m=25π4⋅10896500
6. Final Calculation:
Calculate m:
m=25⋅108⋅π4⋅96500
This can be simplified to find the numerical value.
The equation t2+I2=25 describes a relationship between time t and current I. We can rearrange this to express I in terms of t:
I=√25−t2
We need to calculate the total charge Q that flows through the circuit from t=0 to t=5 seconds. The charge can be calculated using the formula:
Q=∫50I(t)dt=∫50√25−t2dt
The integral ∫√25−t2dt can be solved using trigonometric substitution. Let t=5sin(θ), then dt=5cos(θ)dθ. The limits change from t=0 to t=5 which corresponds to θ=0 to θ=π2.
Q=∫π20√25−(5sin(θ))2⋅5cos(θ)dθ
Simplifying inside the square root:
Q=∫π20√25(1−sin2(θ))⋅5cos(θ)dθ=∫π205⋅5cos2(θ)dθ=25∫π20cos2(θ)dθ
The integral ∫cos2(θ)dθ can be evaluated using the identity:
∫cos2(θ)dθ=12(θ+12sin(2θ))
Evaluating from 0 to π2:
∫π20cos2(θ)dθ=π4
Therefore,
Q=25⋅π4=25π4
According to Faraday's law, the amount of substance deposited is given by:
m=Q⋅MF
where M is the molar mass of silver (Ag = 108 g/mol) and F is Faraday's constant (F=96500C/mol):
m=25π4⋅10896500
Calculate m:
m=25⋅108⋅π4⋅96500
This can be simplified to find the numerical value.
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - ELECTROCHEMISTYEXERCISE - Conductance and Kohlrausch s law40videos
ELECTROCHEMISTY
- BOOK - GRB PUBLICATIONCHAPTER - ELECTROCHEMISTYEXERCISE - Reasoning type28videos
ELECTROCHEMISTY
- BOOK - GRB PUBLICATIONCHAPTER - ELECTROCHEMISTYEXERCISE - Thermodynamics in Electrochemistry22videos
ELECTROCHEMISTY
- BOOK - GRB PUBLICATIONCHAPTER - D-BLOCK ELEMENTSEXERCISE - Subjective Type18videos
D-BLOCK ELEMENTS
- BOOK - GRB PUBLICATIONCHAPTER - ENVIRONMENTAL CHEMISTRY EXERCISE - Straight objective type40videos
ENVIRONMENTAL CHEMISTRY
Similar Questions
Knowledge Check
- Question 1 - Select One
The flux in a closed circuit of resistance 20Ω varies with time according to the equation ϕ=6t2−5t+1. What is the induced current at time t=0.25 second?
A0.5 AB0.4 AC0.1 AD0.2 A - Question 2 - Select One
A current in a wire is given by the equation, . I=2t2−3t+1, the charge through cross section of : wire in time interval t=3s to t=5s is
A32.33CB43.34CC45.5CD42C - Question 3 - Select One
The current flowing through wire depends on time as, I=3t2+2t+5
The charge flowing through the cross - section of the wire in time t=0 to t=2 second isA22CB20CC18CD5C
If a charge flowing through a cross section of wire can be written as q=5t2+8tC, then calculate the electric current at t=0 and t=2s. Calculate the amount of charge that must have flown in the interval of 2 seconds starting from t=0 and also calculate the average electric current for this interval.
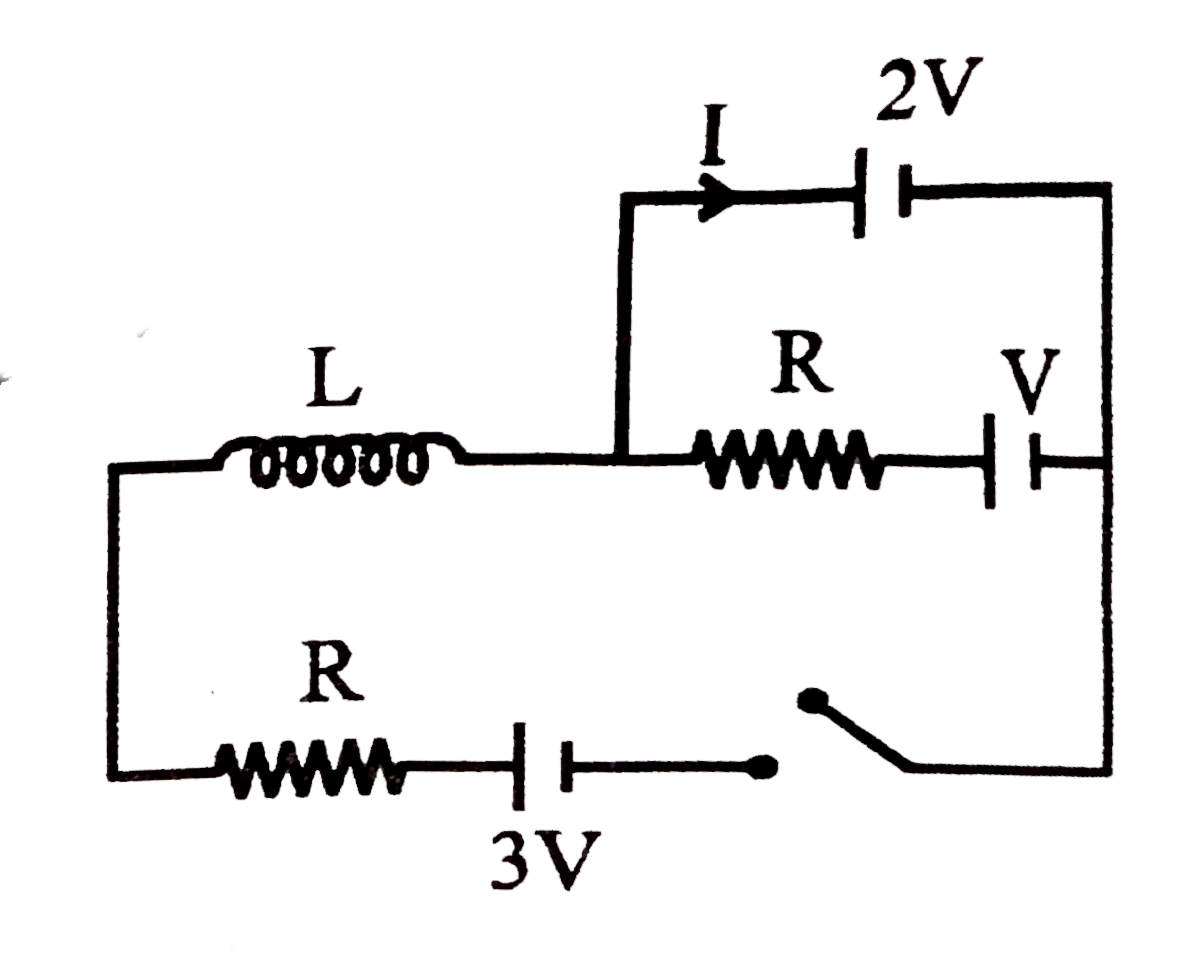
View SolutionIn the LR circuit shown, what is the variation of the current I as a function of time? The switch is closed at time t=0 sec.
 View Solution
View SolutionThe flux of magnetic field through a closed conducting loop of resistance 0.4Ω changes with time according to the equation Φ=0.20t2+0.40t+0.60 where t is time in seconds.Find (i)the induced emf at t=2s.(ii)the average induced emf in t=0 to t=5s.(iii)charge passed through the loop in t=0 to t=5s (iv)average current.In time interval t=0 to t=5s (v) heat produced in t=0 to t=5s
View SolutionThe current in a coil self inductance 2.0 H is increasing according to i=2sint2 amp. Find the amount of energy spent during the period when current changes from to 2 A.
View SolutionThe magnetic flux passing through a metal ring varies with time t according to ϕB=6t3−I8t2 , t is in second. The resistance of the ring is 3Ω . Determine the maximum current induced in the ring during the interval from t=0 to t=2sec .
View Solution