Decomposition of NH4NO2(aq into N2(g) and 2H2O(l) is first order reaction.
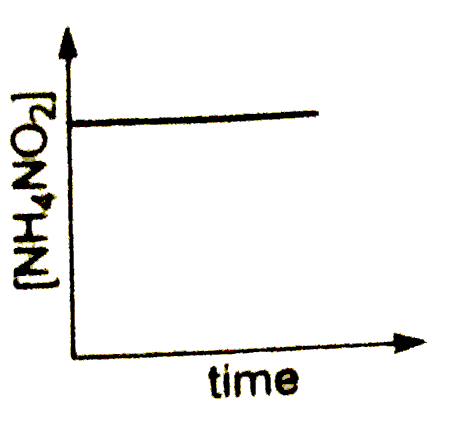

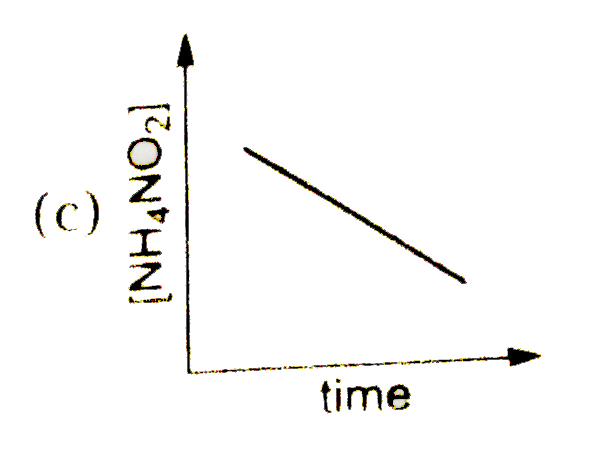
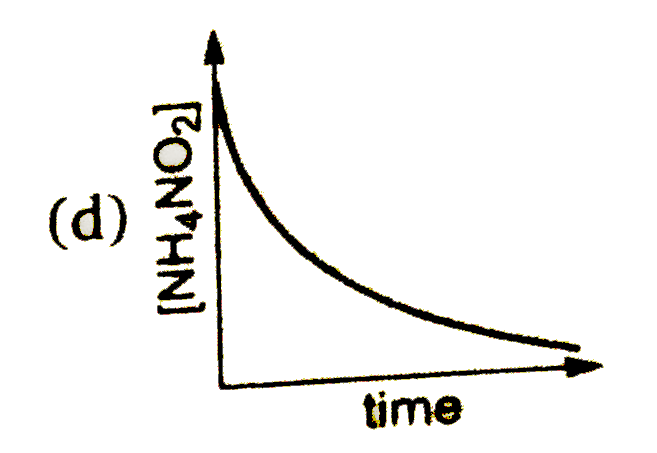
The correct Answer is:D
To solve the problem regarding the decomposition of ammonium nitrite (NH₄NO₂) into nitrogen gas (N₂) and water (H₂O), we need to analyze the reaction and its characteristics as a first-order reaction. Here’s a step-by-step solution:
Step 1: Write the Reaction
The decomposition reaction can be represented as:
NH4NO2(aq)→N2(g)+2H2O(l)
Step 2: Identify the Order of the Reaction
The problem states that this is a first-order reaction. In a first-order reaction, the rate of reaction is directly proportional to the concentration of one reactant.
Step 3: Write the Rate Law
For a first-order reaction, the rate law can be expressed as:
Rate=−d(NH4NO2)dt=k(NH4NO2)
where k is the rate constant.
Step 4: Integrate the Rate Law
To find the relationship between concentration and time, we need to integrate the rate law. Rearranging gives:
d(NH4NO2)(NH4NO2)=−kdt
Integrating both sides:
∫d(NH4NO2)(NH4NO2)=−k∫dt
This results in:
ln(NH4NO2)=−kt+C
Where C is the integration constant. At t=0, let (NH4NO2)=(NH4NO2)0:
ln(NH4NO2)0=C
Substituting back gives:
ln(NH4NO2)=−kt+ln(NH4NO2)0
Step 5: Exponential Form
Exponentiating both sides to eliminate the natural logarithm yields:
(NH4NO2)=(NH4NO2)0e−kt
Step 6: Graphical Representation
The concentration of NH₄NO₂ decreases exponentially over time. The graph of concentration vs. time for a first-order reaction will show a downward curve, indicating that as time increases, the concentration of NH₄NO₂ decreases.
Step 7: Identify the Correct Graph
Based on the characteristics of a first-order reaction, the graph will be an exponential decay curve. Among the options provided, the correct graph will be the one that shows a decreasing exponential trend.
Conclusion
The correct answer is the graph that represents an exponential decrease in concentration over time.
---
The decomposition reaction can be represented as:
NH4NO2(aq)→N2(g)+2H2O(l)
The problem states that this is a first-order reaction. In a first-order reaction, the rate of reaction is directly proportional to the concentration of one reactant.
For a first-order reaction, the rate law can be expressed as:
Rate=−d(NH4NO2)dt=k(NH4NO2)
where k is the rate constant.
To find the relationship between concentration and time, we need to integrate the rate law. Rearranging gives:
d(NH4NO2)(NH4NO2)=−kdt
∫d(NH4NO2)(NH4NO2)=−k∫dt
ln(NH4NO2)=−kt+C
ln(NH4NO2)0=C
ln(NH4NO2)=−kt+ln(NH4NO2)0
Exponentiating both sides to eliminate the natural logarithm yields:
(NH4NO2)=(NH4NO2)0e−kt
The concentration of NH₄NO₂ decreases exponentially over time. The graph of concentration vs. time for a first-order reaction will show a downward curve, indicating that as time increases, the concentration of NH₄NO₂ decreases.
Based on the characteristics of a first-order reaction, the graph will be an exponential decay curve. Among the options provided, the correct graph will be the one that shows a decreasing exponential trend.
The correct answer is the graph that represents an exponential decrease in concentration over time.
Topper's Solved these Questions
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.3 To Q.32)
2 Videos
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.33 To Q.62)
3 Videos
- SURFACE CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level 3 - Assertion - Reason Type Questions
1 Videos
Similar Questions
The decomposition of N2O5 according to the equation 2N2O5(g)→4NO2(g)+O2(g) is a first order reaction. After 30 min. from start of decomposition in a closed vessel the total pressure developed in found to be 284.5 mm Hg. On complete decomposition, the toal pressure is 584.5 mm Hg. Calculate the rate constant of the reaction.
View SolutionThe molar heat of formation of NH4NO3(s) is −360.0kJ and those of N2O(g)and H2O(l) are +80.00kJ and −285.00kJ, respectively, at 25∘C and 1atm. Calculate ΔH and ΔU for the reaction.
NH4NO3(s)→N2O(g)+2H2O(l)
View Solution
Knowledge Check
Decomposition of NH4NO2(aq into N2(g) and 2H2O(l) is first order reaction.
A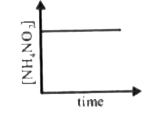 B
B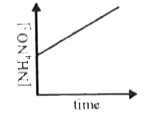 C
C D
D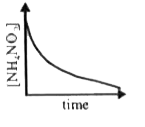
The gas phase reaction 2NO2(g)→N2O4(g) is an exothermic reaction. The decomposition of N2O4 in equilibrium mixture of NO2(g)andN2O4 can be increased by :
Alowering the temperatureBincreasing the pressureCaddition of an inert gas at constant volumeDaddition of an inert gas at constant pressureNH4NO3Δ−−→N2O+H2O
AFor disproportionation reaction.BFor comproportionation reaction.CFor either intermolecular redox reaction or displacement reactionDFor either thermal combination redox reaction or thermal decomposition redox reaction.
The molar heat of formation of NH4NO3(s) is −367.5kJ and those of N2O(g) and H2O(l) are +81.46kJand−285.78kJ respectively at 25∘C and 1 atmospheric pressure. Calculate the ΔH and ΔU for the reaction,
NH4NO3(s)→N2O(g)+2H2O(l)
View SolutionThe molar heat of formation of NH4NO3(s) is −367.5kJ and those of N2O(g) and H2O(l) are +81.46kJand−285.78kJ respectively at 25∘C and 1 atmospheric pressure. Calculate the ΔH and ΔU for the reaction,
NH4NO3(s)→N2O(g)+2H2O(l)
View SolutionIn the reaction NH4NO2(aq.)→N2(g)+2H2O(l) the volume of N2 after 20 min and after a long time is 40ml and 70ml respectively, The value of rate constant is :
View SolutionIn the reaction NH4NO2(aq.)→N2(g)+2H2O(l) the volume of N2 after 20 min and after a long time is 40ml and 70ml respectively, The value of rate constant is :
View SolutionIn the reaction NH4NO2(aq.)→N2(g)+2H2O(l) the volume of N2 after 20 min and after a long time is 40ml and 70ml respectively, The value of rate constant is :
View Solution
