For the reaction
(i) AkI−−→P
(ii) BKII−−→Q, following observation is made.
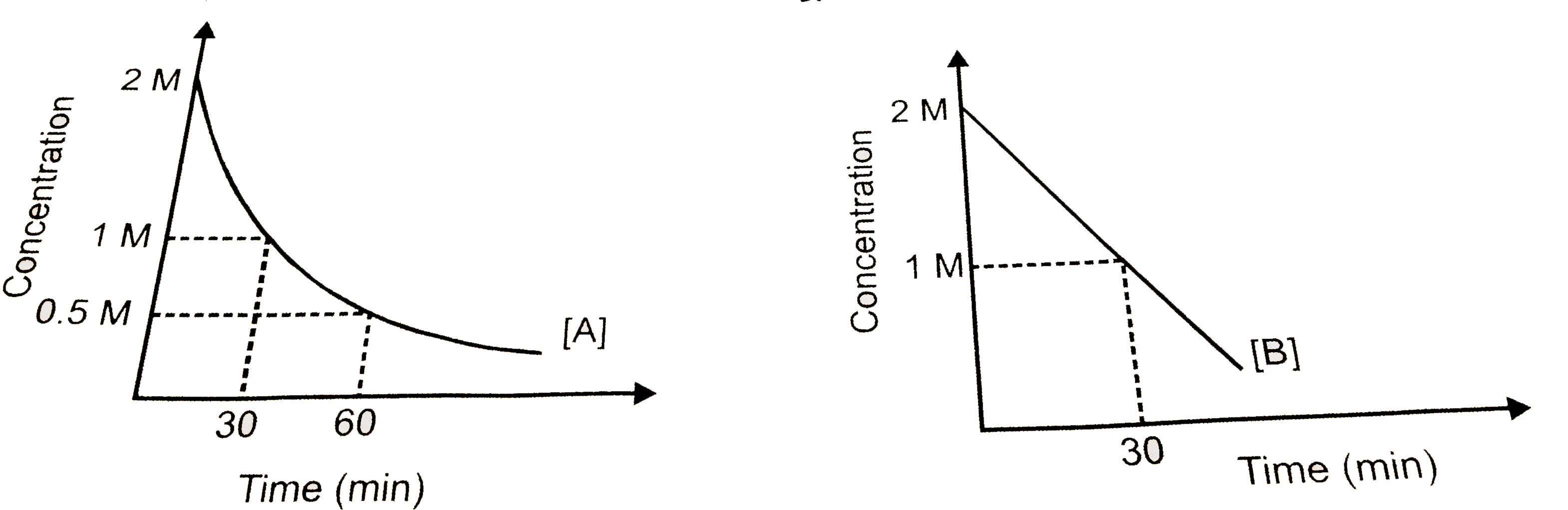
Calculate k1kII, where kI and kII and rate constant for the respective reaction.
2.303
1
0.36
0.693
The correct Answer is:D
Step by step video, text & image solution for For the reaction (i) Aoverset(k_(I))toP (ii) Boverset(K_(II))toQ, following observation is made. Calculate (k_(1))/(k_(II)), where k_(I) and k_(II) and rate constant for the respective reaction. by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.3 To Q.32)2videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.33 To Q.62)3videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level 3 - Assertion - Reason Type Questions1videos
SURFACE CHEMISTRY
Similar Questions
Conisder parallel reaction:
Ak1−−→B,2Ak2−−→C+D
What would be the rate expresison for [A] ?View Solution60.A consecutive reaction occurs with two equilibria which co-exist together Pk1k2Qk3k4R Where k1,k2,k3 and k4 are rate constants.Then the equilibrium constant for the reaction P ↔ R is
(1) (k1⋅k2)/(k3⋅k4)
(2) (k1⋅k4)/(k2k3)
(3) k1*k2*k3⋅k4
(4) (k1⋅k3)/(k2k4)]]View Solution
Knowledge Check
- Question 1 - Select One
For the reaction
(i) Ak1−−→P
(ii) BkII−−→Q, following observation is made.
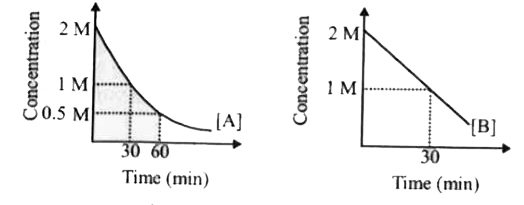
Calculate kIkII, where kI and kII are rate constant for the respective reaction.A2.303B1C0.36D0.693 - Question 2 - Select One
For the reactions (i) AKI−−→P and (ii) BKII−−→Q, following observation is made.
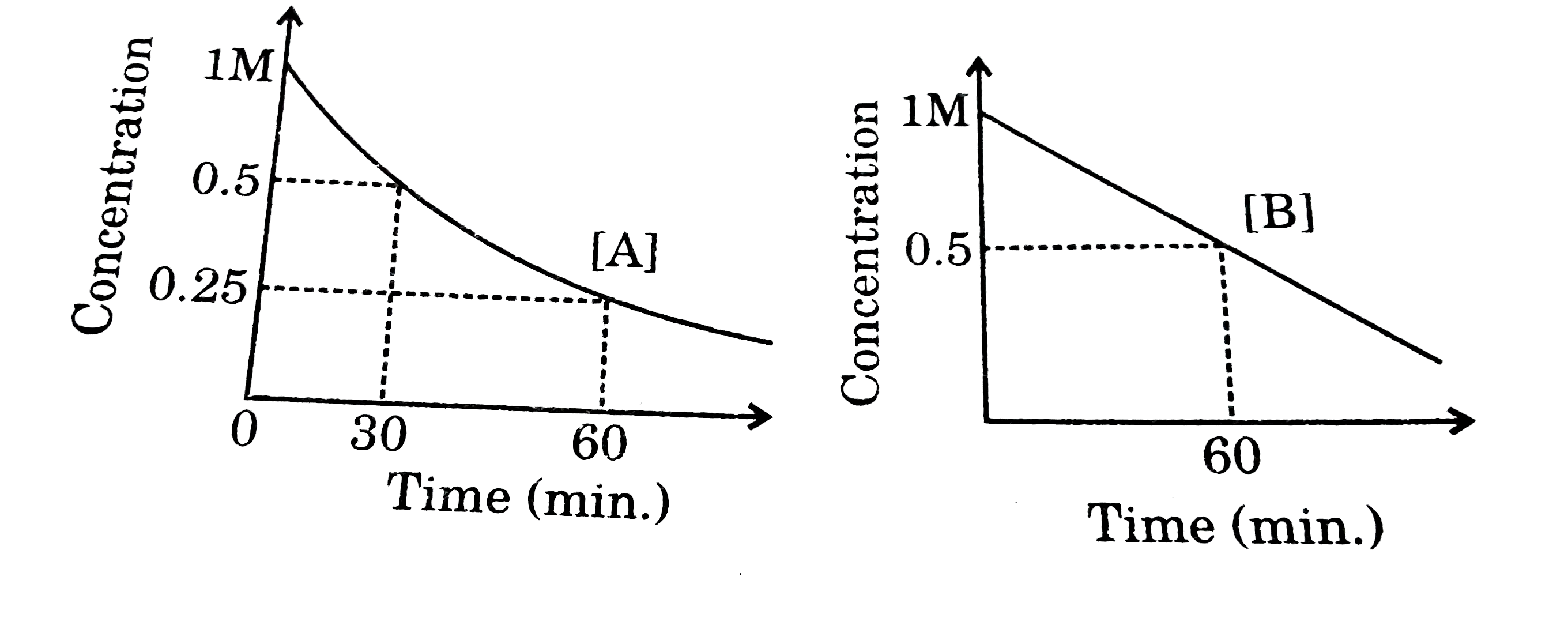
Calculate KIKII where KI and KII are rate constants for the respective reaction.A2.772B1C0.36DNone of these - Question 3 - Select One
For the processes K+(g)I−−→K(g)II−−→K(s)
Aenergy is released in (I) and absorbed in (II)Benergy is absorbed in (I) and released in (II)Cenergy is absorbed in both the processesDenergy is released in both the processes
For the reaction of I, II and III orders, k1=k2=k3 when concentrations are expressed in mole L−1. What will be the relation in k1,k2,k3, if the concentration are expressed in molmL−1?
View SolutionConsider the following hypothetical reactions
Ak1⇐⇒k2B , Bk3−−→slowC
The overall rate constant kθ of the reaction isView SolutionIf a unimolecular reaction, A(g)→ Products, takes place according to the mechanism
(I)A+Ak1⇐===⇒k−1Aa+A
(II)Aa−−→k2P
where k1, k−1 and k2 are the rate constants and P,A and Aa stand for product molecule, normal molecule of reactant and activated molecules of reactant and activated molecules of reactant respectively.
For the reaction scheme, X+Ykf⇐===⇒kbZ, Y+Zk−−→T, the rate equation for the formation of T will beView SolutionIf a unimolecular reaction, A(g)→ Products, takes place according to the mechanism
(I)A+Ak1⇐===⇒k−1Aa+A
(II)Aa−−→k2P
where k1, k−1 and k2 are the rate constants and P,A and Aa stand for product molecule, normal molecule of reactant and activated molecules of reactant and activated molecules of reactant respectively.
The order 'n' initial concentration a0 and time of half reaction t1/2, for a reaction are related asView SolutionIf a unimolecular reaction, A(g)→ Products, takes place according to the mechanism
(I)A+Ak1⇐===⇒k−1Aa+A
(II)Aa−−→k2P
where k1, k−1 and k2 are the rate constants and P,A and Aa stand for product molecule, normal molecule of reactant and activated molecules of reactant and activated molecules of reactant respectively.
Which of the following expressions are correct?View Solution

