A circuit consists of a coil, a switch and a battery, all in series. The interval resistance of the battery is negligible compared with that of the coil. The switch is originally open. It is thrown closed, after a time interval Δt. The current in the circuit reaches 80.0% of its final value. The switch then remains closed for a time interval much longer than Δt. The wires connected to the terminals of the battery are then short circuited with another wire and removed from the battery, so that the current is uninterrupted.
At an instant that is a time interval Δt. After the short circuit, the current is what percentage of its maximum value?
20.0%
8.0%
4.0%
10.0%
The correct Answer is:A
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Concept Based
9 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICSCHAPTER - INDUCTANCEEXERCISE - Multiple Correct Answer
3 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICSCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
28 Videos
- KINETIC THEORYBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORYEXERCISE - Question Bank
31 Videos
Similar Questions
Determine the current through the battery in the circuit shown in figure.
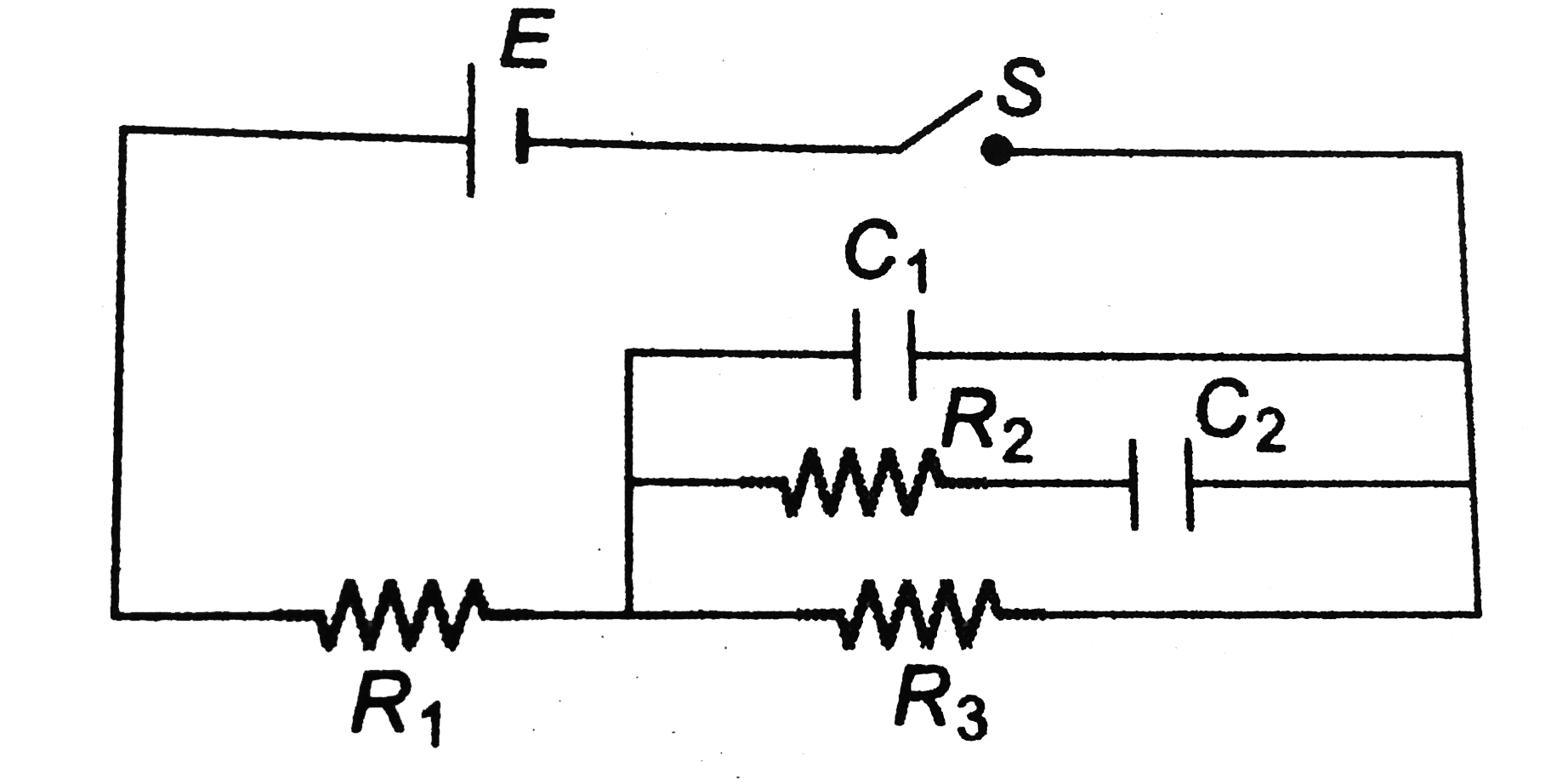
(a) immediately after the switch S is closed
(b) after a long time.
View SolutionDetermine the current through the battery in the circuit shown in figure.

(a) immediately after the switch S is closed
(b) after a long time.
View Solution
Knowledge Check
A circuit consists of a coil, a switch and a battery, all in series. The interval resistance of the battery is negligible compared with that of the coil. The switch is originally open. It is thrown closed, after a time interval Δt. The current in the circuit reaches 80.0% of its final value. The switch then remains closed for a time interval much longer than Δt. The wires connected to the terminals of the battery are then short circuited with another wire and removed from the battery, so that the current is uninterrupted.
At the moment 2Δt after the coil is short-circuited, the current in the coil is what percentage of its maximum value?A20.0%B8.0%C4.0%D10.0%The circuit shown consists of a switch (S), a battery (B) of emf E, a resistance R, and an inductor L.

The current in the circuit at the instant the switch is closed is-AE/RBE/R(1−e)C∞D0In the circuit as shown in figure the switch is closed at t=0.

A long time after closing the switchAvoltage drop across the capacitor is EBcurent through the battery is E/R1+R2Cenegru stores in the capacitor is
12C(R2ER1+R2)2Dcurrent through the capacitor becomes zero
A circuit consists of three identical lamps connected to a battery as shown in figure. When the switch S is closed then the intensities of lamps A and B
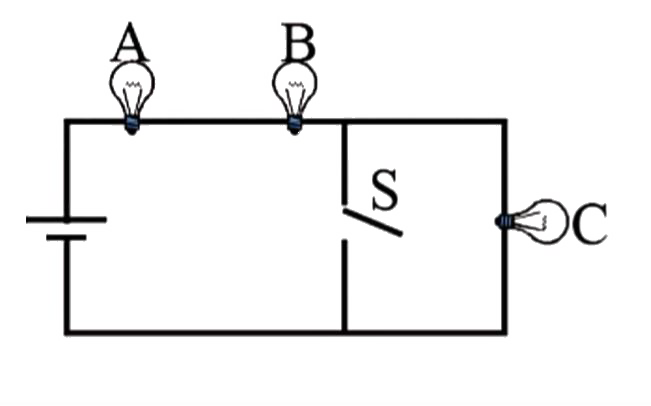
View SolutionA circuit consists of three identical lamps connected to a battery as shown in the figure. When the switch S is closed then the intensities of lamps A and B
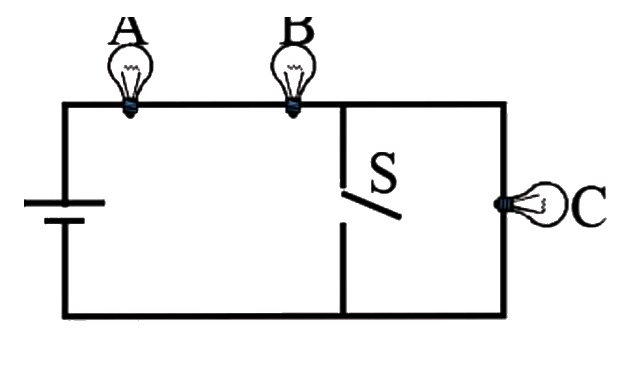
View SolutionA circuit consists of three identical lamps connected to a battery as shown in the figure. When the switch S is closed then the intensities of lamps A and B

View SolutionIn the circuit diagram the current through the battery immediately after the switch S is closed is
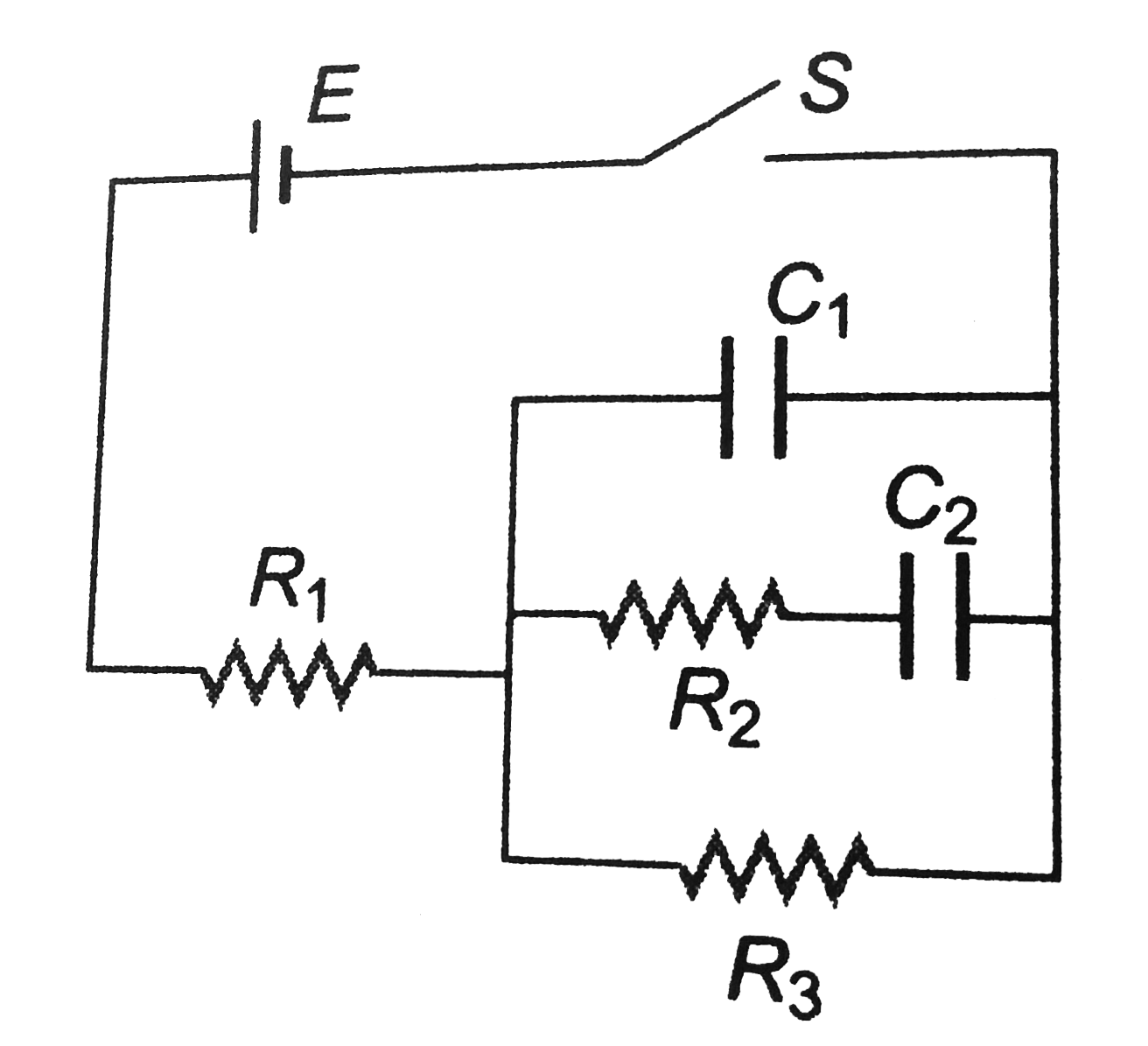
View SolutionIn the circuit diagram the current through the battery immediately after the switch S is closed is

View Solution
