Find the locus of the points where the intensity of the magnetic field due to a magnetic dipole will be perpendicular to its axis.
The correct Answer is:At 54∘42' with the axis of the dipole
Step by step video, text & image solution for Find the locus of the points where the intensity of the magnetic field due to a magnetic dipole will be perpendicular to its axis. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Find the locus of points where the electric field due to a dipole is (i) perpendicular to its axis , (ii) anti-parallel to the axis .
[Hint : tanα=tanθ2]View SolutionThere is one short electric dipole placed on a horizontal plane. A circle is drawn assuming centre of dipole as centre of circle and plane of the circle is perpendicular to the axis of electric dipole. Thế number of points on this circle where electric field intensity due to electric dipole is perpendicular to the axis of dipole.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic induction at any point due to a short magnetic dipole is
Aπ04πMr3√3cos2θ+1Bπ04π2Mr2√3cos2θ+1Cπ04π√3cos2θ+1Dπ04π2Mr3√3cos2θ+1 - Question 2 - Select One or More
Consider the situation of the previous problem. The directions of the magnetic field due to the dipole are opposite at
Aa tangent galvanometerBa diflection galvanometer if the earth's horizontal field is knownCan oscillation magnetometer if the earth's horizontal field is knownDboth diflection and oscillation magnetometer if the earth's horizontal field is not known. - Question 3 - Select One
Intensity of magnetic field due to earth at a point inside a hollow steel box is
ALess than outsideBMore than outsideCsameDZero
What is the potential energy of a magnetic dipole when it is placed perpendicular to the magnetic field?
View SolutionA short bar magnet having magnetic dipole moment M is moving along the axis of a fixed conducting (non magnetic) ring of radius R. The axis of the ring is along z direction.
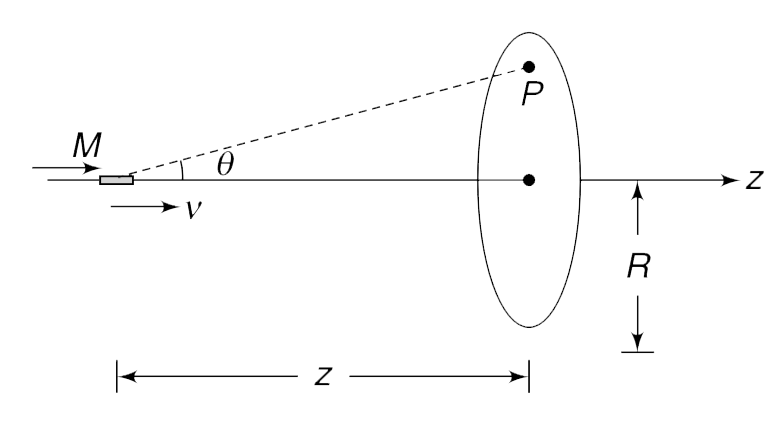
(a) Write the z component of magnetic field due to the magnetic dipole at a point P in the plane of the ring, at the instant the magnet is at a distance z from the centre of the ring. Position of point P can be defined in terms of angle θ as shown.
(b) Write the magnetic flux through the ring due to the magnetic field produced by the magnet as a function of z.
(c) Write the magnitude of emf induced in the ring at the instant shown if speed of the magnet at the moment is v.View SolutionThe ratio of the electric field due to an electric dipole on its axis and on the perpendicular bisector of the dipole is -
View SolutionThe magnetic potential at any point due to short magnetic dipole is
View SolutionThe locus of the points (in the xy-plane) where the electric field due to a dipole (dipole axis is along x-axis and its equatorial is along y-axis) is perpendicular to its axis, is
View Solution

