A horizontal cylindrical vessel with a small orifice of area s is first filled with a liquid of density and then forced out through it by applying a constant force on the piston closing the cylinder. The time taken is t. The time taken is t. Calculate the work done.
The correct Answer is:
Step by step video, text & image solution for A horizontal cylindrical vessel with a small orifice of area s is first filled with a liquid of density rho and then forced out through it by applying a constant force on the piston closing the cylinder. The time taken is t. The time taken is t. Calculate the work done. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.

View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View Solution
Knowledge Check
A liquid of density ρ is filled in two indentical cylindrical vessels with base area A and height of the liquid in one vessel is h1 and that in the other vessel is h2. If both the vesels are connected with their base at the same level then calculate the work done by gravity in equalizing the levels.
A(h1−h2)gρB(h1−h2)gAρC12(h1−h2)2gAρD14(h1−h2)2gAρFigure shows a semi-cylindrical massless gate pivoted at the point O holding a stationary liquid of density ρ. The length of the cylinder is l. Calculate, the horizontal force exerted by the liquid on the gate.
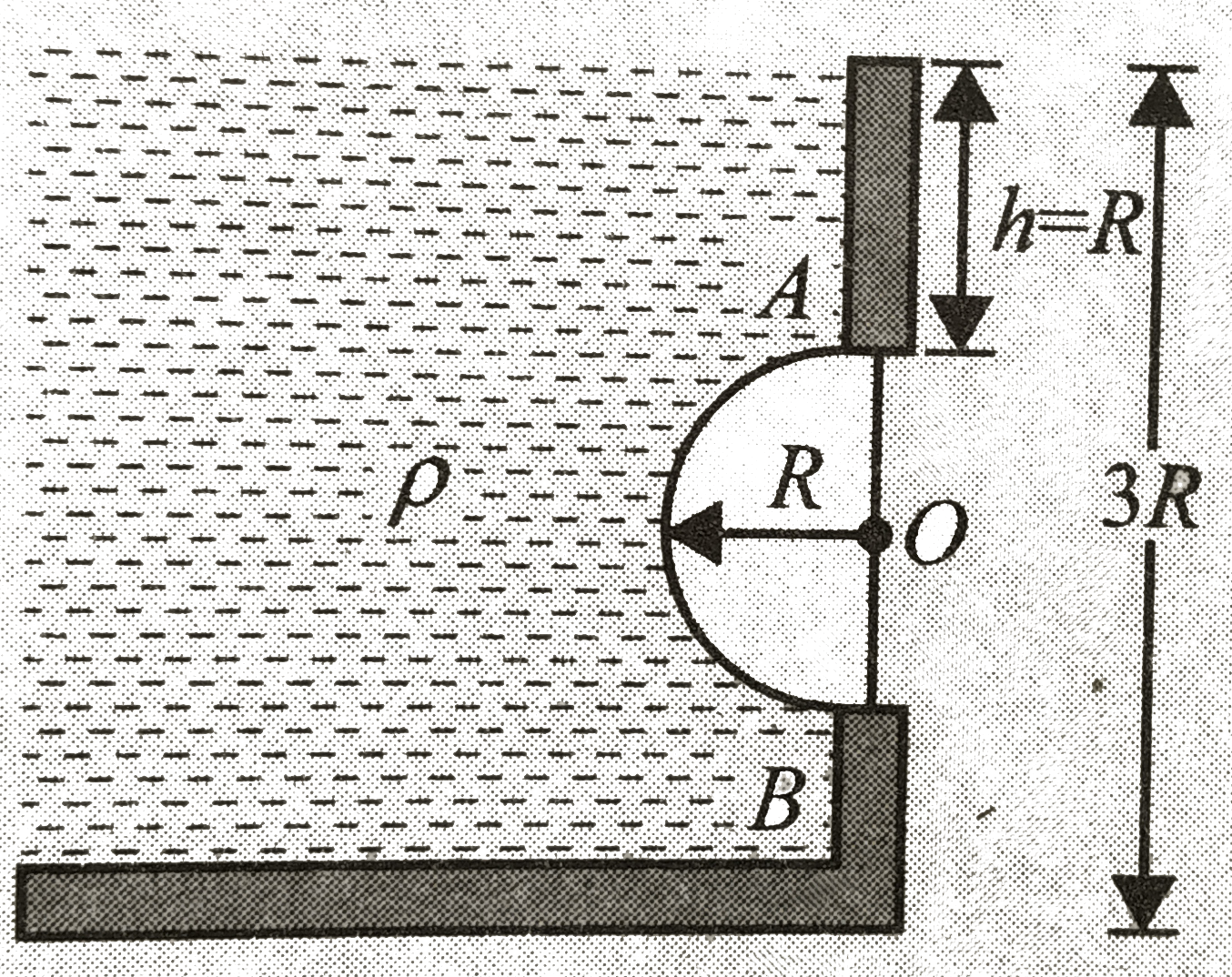 A4ρgR2lBρgR2lC4ρgR3lDnone
A4ρgR2lBρgR2lC4ρgR3lDnoneA cylindrical vessel of area of cross-section A and filled with liquid to a height of h1 has a capillary tube of length l and radius r protuding horizontally at its bottom. If the viscosity of liquyid is η and density ρ. Find the time in which the level of water in the vessel falls to h2.
A8ηlAπρgr4 ln h1h2B8ηlAπρgr4CηAg(√h1−√h2)D8ηlAπρgr4 ln h2h1
A small ball of mass m and density ρ is dropped in a viscous liquid of density σ. Ather some time the ball falls with a constant velocity. Calculate the viscous force acting on the ball.
View SolutionA large vessel of height H is filled with a liquid of density ρ upto the brim. A small hole of radius r is made at the side vertical face, close to the base. The horizontal force is required to stop the gushing of liquid is
View SolutionA horizontal cylinder of length l contains water. On the left a constant force F is applied on the piston and on the right there is a small hole of area a. What is the velocity of the piston? Hence, calculate the work done in emptying the vessel in time t. brgt
 given area of cylinder is A
given area of cylinder is A
View SolutionA pump is designed as a horizontal cylinder with a piston of areal A and and outlet orifice of areal a arranged mear the cylinder axis. Find the velocity of out flow of the liquid from the pump if the piston moves with a constant velocity under the action of a constant force F. The density of the liquid is ρ.
View SolutionA body of mass 0.25 kg moving with velocity 12m/s is stopped by applying a force of 0.6 N. Calculate the time taken to stop the body. Also calculate the impulse of this force.
View Solution