Two springs of force constants k1 and k2 are joined together and the combination is attached to a mass m resting on a frictionless table at one end and clamped to a fixed support at the other. Show the frequency of oscillation of the mass is f=12π√k1k2(k1+k−(2))m
[Hint: Let the mass be displaced by x and the clamped end of the second spring by x′. Then mf = −k1(x−x′). Considering the first spring and the mass as a single system we have mf =−k2x′]
The correct Answer is:NA
Step by step video, text & image solution for Two springs of force constants k_(1) and k_(2) are joined together and the combination is attached to a mass m resting on a frictionless table at one end and clamped to a fixed support at the other. Show the frequency of oscillation of the mass is f = 1/(2pi)sqrt((k_(1)k_(2))/((k_(1) + k-(2)))m [Hint: Let the mass be displaced by x and the clamped end of the second spring by x^('). Then mf = -k_(1)(x-x^(')). Considering the first spring and the mass as a single system we have mf =-k_(2)x^(')] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - NN GHOSHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Eexercies39videos
SIMPLE HARMONIC MOTION
- BOOK - NN GHOSHCHAPTER - SIMPLE AND COMPOUND PENDULUMEXERCISE - Exercise24videos
SIMPLE AND COMPOUND PENDULUM
- BOOK - NN GHOSHCHAPTER - SPECIFIC HEAT CAPACITY OF GASESEXERCISE - All Questions17videos
SPECIFIC HEAT CAPACITY OF GASES
Similar Questions
Two springs of force constants k1 and k2 are attached to two opposite sides of a cube of mass m resting on a frictionless table and clamped to two supports at their other ends. Show that if the cube is displaced a little it will execute simple harmonic motion of frequency f=12π√k1+k2m
View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two spring of spring constant k1 and k2 are joined in series The effective spring constant of the combination is given by
A√k1k2B(k1+k2)/2Ck1+k2Dk1k2k1+k2 - Question 2 - Select One
Two springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
A√k1k2B(k1+k2)2Ck1+k2Dk1k2(k1+k2) - Question 3 - Select One
Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 View Solution
View SolutionTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
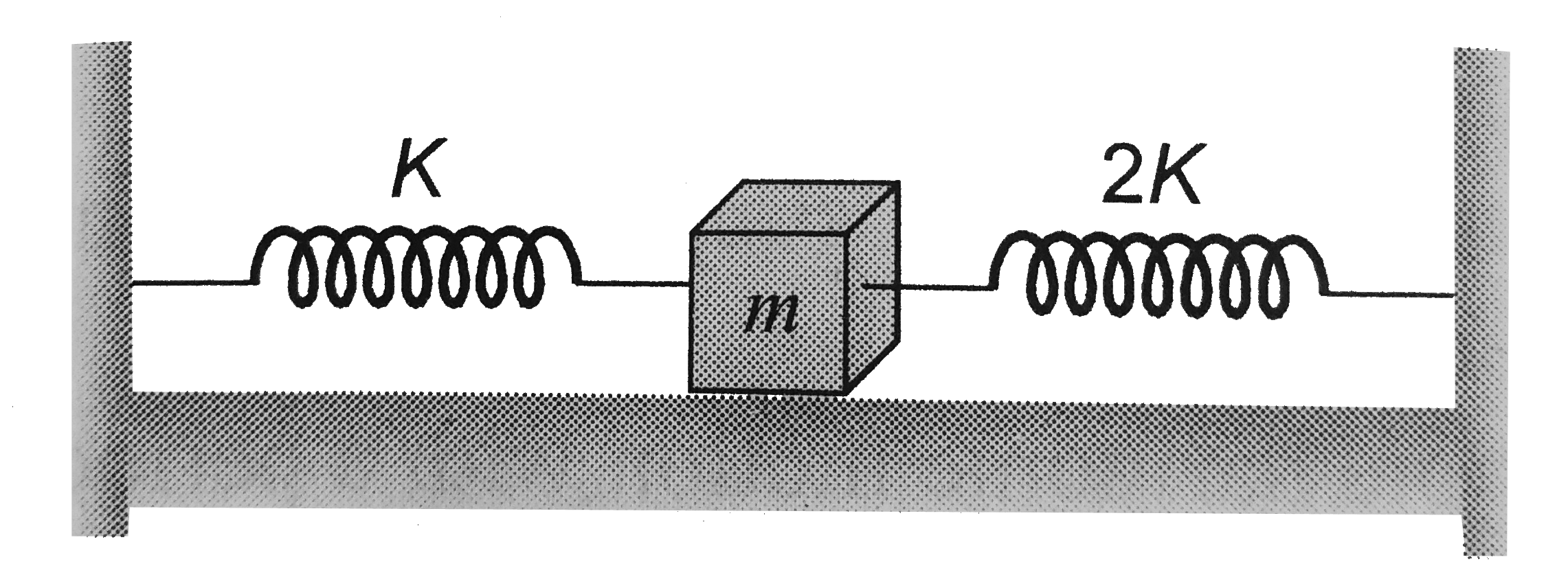 View Solution
View SolutionTwo springs have their force constant as k1 and k2(k1>k2). When they are stretched by the same force.
View SolutionTwo springs of force constants k1 and k2, are connected to a mass m as shown. The frequency of oscillation of the mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
_E01_383_Q01.png) View Solution
View SolutionTwo springs, of force constants k1 and k2, are connected to a mass maas shown. The frequency of oscillation of mass is f. If both k1 and k2 are made four times their original values, the frequency of oscillation becomes
 View Solution
View Solution

