A thin rod is clamped at one end to the wall of a vessel, while the other end is submerged in water. The rod can ratate freely about the horizontal axis at A, which is above the water level. Find the density p of the rod is not submerged in the water
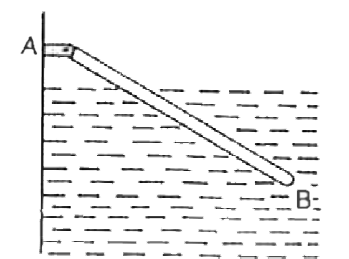
Step by step video & image solution for A thin rod is clamped at one end to the wall of a vessel, while the other end is submerged in water. The rod can ratate freely about the horizontal axis at A, which is above the water level. Find the density p of the rod is not submerged in the water by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
A charge of 1 coul. is placed at one end of a non-conducting rod of length 0.6m. the rod is rotated in a vertical plane about a horizontal axis passing through the other end of the rod with angular frequency 104πradian/sec. Find the magnetic field at a point on the axis ofrotation at a distance of 0.8 from the centre of the path. Now half of the charge is removed from one end and placed on the other end. The rod is rotated in a vertical plane about horizontal axis passing through the mid-point of the rod with the same angnlar frequency. Calculate the magnetic field at a point on the axis at a distance of 0.4m form the centre of the rod.
View SolutionA rod of length 6m has a mass of 12kg. It is hinged at one end of the rod at a distance of 3m below the water surface.
a. What must be the weight of a block that is attached to the other end of the rod so that 5m of the rod's length is under water?
b. Find the magnitude and direction of the force exerted by the hinge on the rod. The specific gravity of the material of rod is 0.5.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A weightless rod of length l carries two equal masses m one fixed at the end and other in the middle ofhte rod. The rod can revolve in a vertical plane about A. Then, horizontal velocity which must be imparted to end C of rod to deflect it to horizontal position is
 A√125glB√3glC√165glD√2gl
A√125glB√3glC√165glD√2gl - Question 2 - Select One
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotation - Question 3 - Select One
Two adiabatic vessels, each containing the same mass m of water but at different temperatures, are connected by a rod of length L, cross-section A, and thermal conductivity K. the ends of the rod are inserted into the vessels, while the rest of the rod is insulated so that .there is negligible loss of heat into the atmosphere. The specific heat capacity of water is s, while that of the rod is negligible. The temperature difference between the two vessels reduces to l/e of its original value after a time, δt. The thermal conductivity (K) of the rod may be expressed by:
AmsLAδtBemsLAδtCmsL2eAδtDmsL2Aδt
A uniform rod of mass m and length L is fixed to an axis, making an angle θ with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?
 View Solution
View SolutionA light rigid rod has a small ball of mass m attached to its one end. The other end is hinged on a table and the rod can rotate freely in vertical plane. The rod is released from vertical position and while falling the ball at its end strikes a hemisphere of mass m lying freely on the table. The collision between the ball and the hemisphere is elastic. The radius of hemisphere and length of the rod are R and 2R respectively. Find the velocity of the hemisphere after collision.
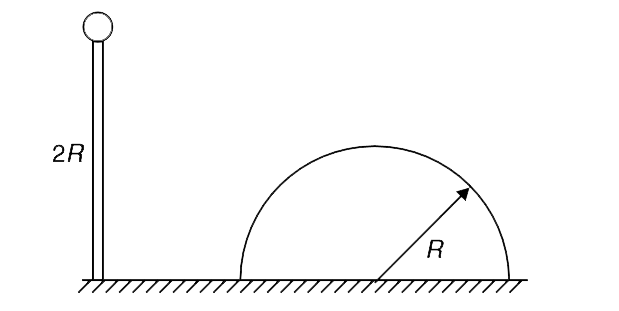 View Solution
View SolutionA rigid rod leans against a vertical wall (y-axis) as shwon in figure. The other end of the rod is ion the horizontal floor. Point A is pushed downwards with constant velocity. Path of the centre of the rod is
 View Solution
View SolutionA rod of length l is siding such that one of its ends is always in contact with a vertical wall and its other end is always in contact with horizontal surface. Just after the rod is relased from rest, the magnitude of acceleration of end points of the rod is and b respectively. The angular acceleration of road at this istant will be
 View Solution
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:View Solution

