the cylinder of a water pump is 4 cm above the surface of water in a well. If the readius of the cylinder of the pump be 5cm, calculate th e force acting on the piston while the pump is working.(Density of water =1000kgm−3)
[ hint : force = area x pressure due to 4-m high column of water .]
The correct Answer is:308 N
Topper's Solved these Questions
Similar Questions
A water pump raises 50 litres of water through a height of 25 m in 5 .Calculate the power of the pump required . (Take g=10 N kg−1 and density of water =1000 kg m−3)
View SolutionA cylinder of relative density 0.7 is 0.5 m high and the radius of its base is 1m . It floats in water with its axis vertical . Find the legth of the cylinder inside water. What force is needed to raise it by 1 cm ? Denstiny of water =1000 kg m−3
View Solution
Knowledge Check
Find the force acting on the pistion of 3cm2 at point 2 due to the water coluum of height 10m.
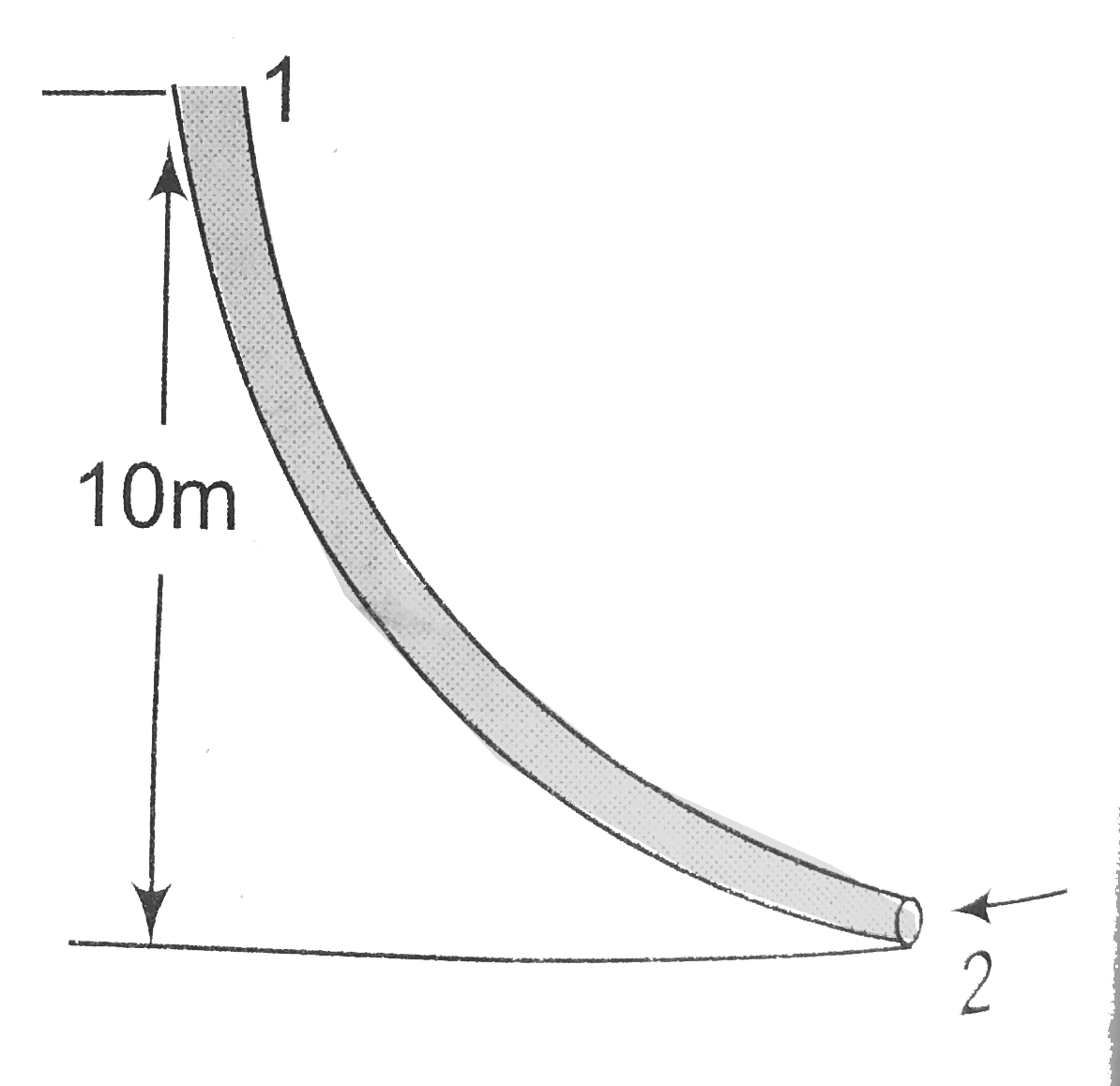 A10 NB20 NC30 ND40 N
A10 NB20 NC30 ND40 NA tube - well pump out 2400 kg of water per minute. If water is coming out with a velocity of 3m/s, the power of the pump is
A120 WB180 WC240 WD90 W
Calculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
View SolutionA tube - well pump out 2400 kg of water per minute. If water is coming out with a velocity of 3m/s, the power of the pump is
View SolutionAn engine can pump 30,000 L of water to a vertical height of 45 m in 10 min. Calculate the work done by the machine and the power. (Density of water = 103kg/m3,1000L−1m3,g=9.8ms−2)
View SolutionA needle of length 3 cm is floating on the surface of water. Calculate the minimum force needed to lift the needle above the surface of water. Surface tension of water is 0.072 N/m.
View SolutionA needle of length 5 cm is floating on the surface of water. Calculate the minimum force needed to lift the needle above the aurface of water. Surface tension of water is 0.073 N/m.
View SolutionThe density of water at 40C is supposed to be 1000kgm−3. It is same at the sea level and at a high altitude?
View Solution
