In a Kater's pendulum the time periods about the knife edges at distance l1andl2 from the centre of gravity are t and t+pi is very small. Show that 4π2(l1+l2)g=t(t+2l2τl2−l1)
Step by step video & image solution for In a Kater's pendulum the time periods about the knife edges at distance l_(1) and l_(2) from the centre of gravity are t and t+pi is very small. Show that (4 pi^(2)(l_(1)+l_(2)))/(g)=t(t+(2l_(2)tau)/(l_(2)-l_(1))) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE AND COMPOUND PENDULUMBOOK - NN GHOSHCHAPTER - SIMPLE AND COMPOUND PENDULUMEXERCISE - Exercise
24 Videos
- SECOND LAW OF THERMODYNAMICSBOOK - NN GHOSHCHAPTER - SECOND LAW OF THERMODYNAMICSEXERCISE - All Questions
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - NN GHOSHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Eexercies
39 Videos
Similar Questions
Knowledge Check
Consider the line L 1 : x 1 y 2 z 1 312 +++ ==, L2 : x2y2z3 123
A0B17√3C413√3D175√3If the time period of a simple pendulum is T=2π√l/g , then the fractional error in acceleration due to gravity is
A4π2ΔlΔT2BΔll−2ΔlTCΔll+2ΔTTDNone of theseIf l1 and l2 are the lengths of a seconds pendulum at the poles and the equator of the earth, then
Al1>l2Bl1<l2Cl1=l2Dl1=0.9l2
If l1,l2 and l3 are the orders of the currents through our nerves, domestic appliances and average lightening, then the correct order of currents is
(1) l1>l2>l3 (2) l1>l3>l2
(3) l1<l2<l3 (4) l1=l2=l3
View SolutionTwo rods of the same area of cross-section, but of length l1 and l2 and conductivites K1 and K2 are joined in series. Show that the combination is equivalent of a material of conductivity K=l1+l2(l1K2)+(l2K2)
View SolutionIf the time period of a pendulum is 1sec, then what is the length of the pendulum at point of intersection of l−T and l−T2 graph.
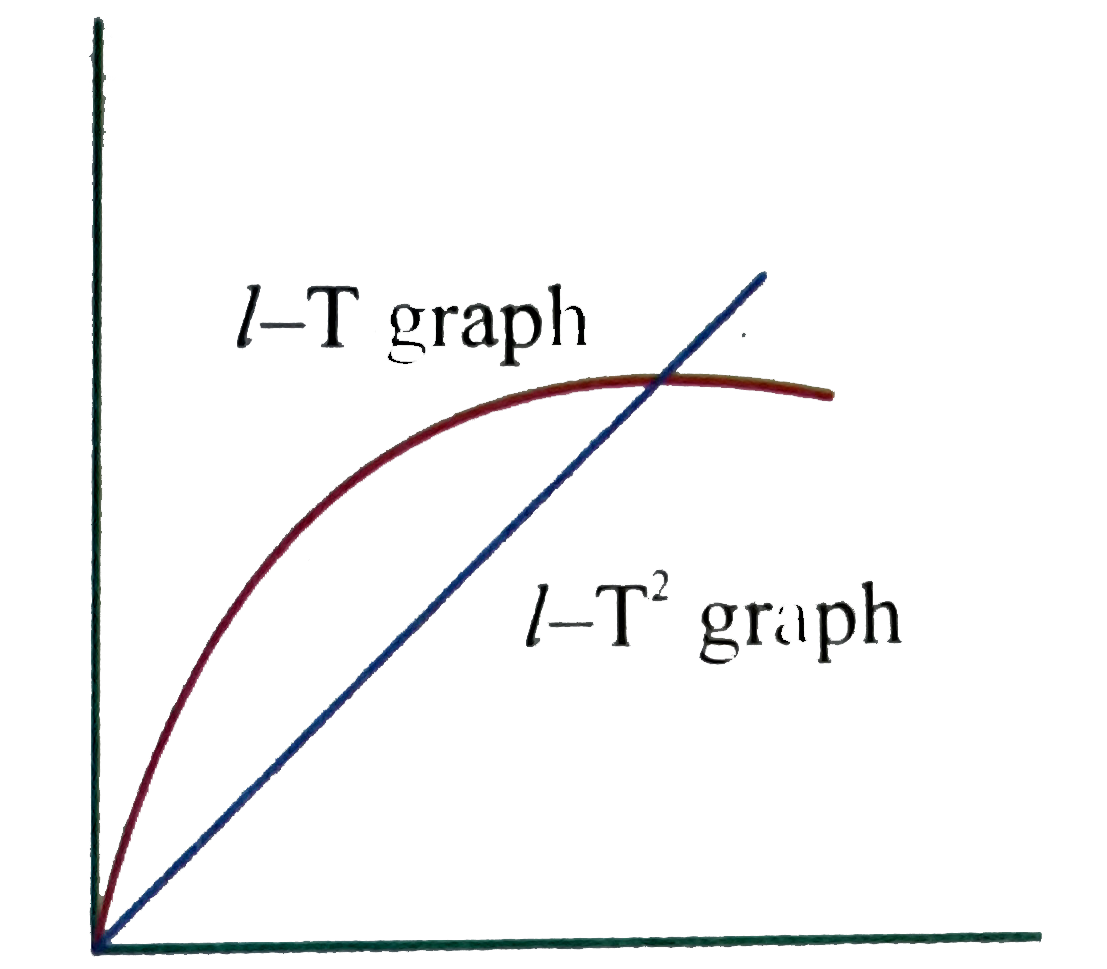
View SolutionThe length of a metal wire is l1 when the tension in it is T1 and is l2 when the tension is T2. Then natural length of the wire is
View SolutionA simple pendulum of length l1 has a time period of 4 s and another simple pendulum of length l2 has a time period 3 s. Then the time period of another pendulum of length (l1−l2) is
View Solution