A steel wire of length 1m and diameter 4mm is stretched horizontally between two rigit supports attached to its end. What load would be required to be hung from the mid-point of the wire to produce a depression of 1cm? (Y=2×1011Nm−2)
The correct Answer is:1.02×104
To solve the problem, we need to determine the load required to produce a depression of 1 cm in a steel wire of length 1 m and diameter 4 mm. We will use the formula for Young's modulus and the relationship between stress, strain, and the applied load.
1. Identify Given Values:
- Length of the wire, L=1m=100cm
- Diameter of the wire, d=4mm=0.004m
- Depression, x=1cm=0.01m
- Young's modulus, Y=2×1011N/m2
2. Calculate the Cross-sectional Area of the Wire:
A=πd24=π(0.004)24=π×0.0000164≈1.2566×10−5m2
3. Calculate the Strain:
Strain (ε) is defined as the change in length (depression) divided by the original length.
Strain(ϵ)=xL=0.011=0.01
4. Calculate the Stress:
Stress (σ) is defined as the force (load) per unit area.
Stress(σ)=Y⋅ϵ
Rearranging gives us:
σ=Y⋅ϵ=(2×1011)⋅(0.01)=2×109N/m2
5. Relate Stress to Load:
The stress can also be expressed in terms of the load (W):
σ=WA
Rearranging gives us:
W=σ⋅A=(2×109)⋅(1.2566×10−5)≈25120N
6. Convert Load to Mass:
To find the mass (m) that corresponds to this load, we use:
W=m⋅g
where g≈9.81m/s2. Rearranging gives:
m=Wg=251209.81≈2564.4kg
Final Answer:
The load required to produce a depression of 1 cm in the steel wire is approximately 25120 N, which corresponds to a mass of about 2564.4 kg.
- Length of the wire, L=1m=100cm
- Diameter of the wire, d=4mm=0.004m
- Depression, x=1cm=0.01m
- Young's modulus, Y=2×1011N/m2
A=πd24=π(0.004)24=π×0.0000164≈1.2566×10−5m2
Strain (ε) is defined as the change in length (depression) divided by the original length.
Strain(ϵ)=xL=0.011=0.01
Stress (σ) is defined as the force (load) per unit area.
Stress(σ)=Y⋅ϵ
Rearranging gives us:
σ=Y⋅ϵ=(2×1011)⋅(0.01)=2×109N/m2
The stress can also be expressed in terms of the load (W):
σ=WA
Rearranging gives us:
W=σ⋅A=(2×109)⋅(1.2566×10−5)≈25120N
To find the mass (m) that corresponds to this load, we use:
W=m⋅g
where g≈9.81m/s2. Rearranging gives:
m=Wg=251209.81≈2564.4kg
The load required to produce a depression of 1 cm in the steel wire is approximately 25120 N, which corresponds to a mass of about 2564.4 kg.
Topper's Solved these Questions
- ELASTICITYBOOK - NN GHOSHCHAPTER - ELASTICITYEXERCISE - EXERCIES (A)
11 Videos
- ELASTICITYBOOK - NN GHOSHCHAPTER - ELASTICITYEXERCISE - EXERCIES(b)
14 Videos
- DOPPLER EFFECTBOOK - NN GHOSHCHAPTER - DOPPLER EFFECTEXERCISE - EXERCISES
24 Videos
- ERRORS AND THEIR MEASUREMENTS BOOK - NN GHOSHCHAPTER - ERRORS AND THEIR MEASUREMENTS EXERCISE - EXERCISES
17 Videos
Similar Questions
A steel wire og lrngth 1 m and diameter 3 mm is stetched horizontally between supports attached at its ends .What load would be required to be hung from the mid -point of the wrie would be required to produeced a depression of 1 cm?
(y=2×1011NM−2,g=9.8ms2)
View SolutionA steel wire of diameter d=1.0mm is stretched horizontally between two clamps located at the distance l=2.0m from each other. A weight of mass m=0.25kg is suspended from the mid-point O of the wire. What will the resulting descent of the point O be in centrimetres?
View Solution
Knowledge Check
A mild steel wire of Length 2L and cross sectional Area A is stretched well within elastic limit, horizontally between two pillars. A man m is suspended from the mid point of the wire strain in the wire is
Ax22L2BxLCx2LDx22LA mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
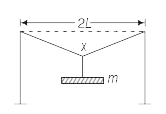 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22LA steel wire of diameter 1 mm, and length 2 m is stretched by applying a force of 2.2 kg wt. the strain is
A0.7×10−4B1.4×10−4C1.9×10−5D2.8×10−4
A steel wire of length 4 m and diameter 5 mm is stretched by kg-wt. Find the increase in its length if the Young's modulus of steel wire is 2.4×1012dynecm−2
View SolutionA mild steel wire of length 1.0m and cross sectional area 5.0×10−2cm2 is stretched, within its elastic limit horizontally between two pillars. A mass of 100g is suspended form the midpont of the wire. Calculate the depression at the midpoint (Ysteel=200GPa)
View SolutionA steel wire of length 4 m and diameter 5 mm is strethed by 5 kg-wt. Find the increase in its length, if the Young's modulus of steel is 2×1012 dyne cm2
View SolutionWhat is the force requiredto stretch a steel wire of 1cm2 cross-section to 1.1 times its length ? (Y=2×1011N/m2)
View SolutionA steel wire of length 1m is stretched between two rigid supports. The wire is vibrating in its fundamental mode with a frequency 100 Hz. The maximum acceleration at the mid point of the wire is 986 m/s2 . Then the amplitude of vibration at the midpoint is
View Solution
