At t=0, a positively charged particle of mass m is projected from the origin with velocity u0 at an angle 37∘ fromn the x-axis as sown in the figure-4.235. a constant →B0=B0ˆj is present in space. After a time internal t0 velocity of particle may be:
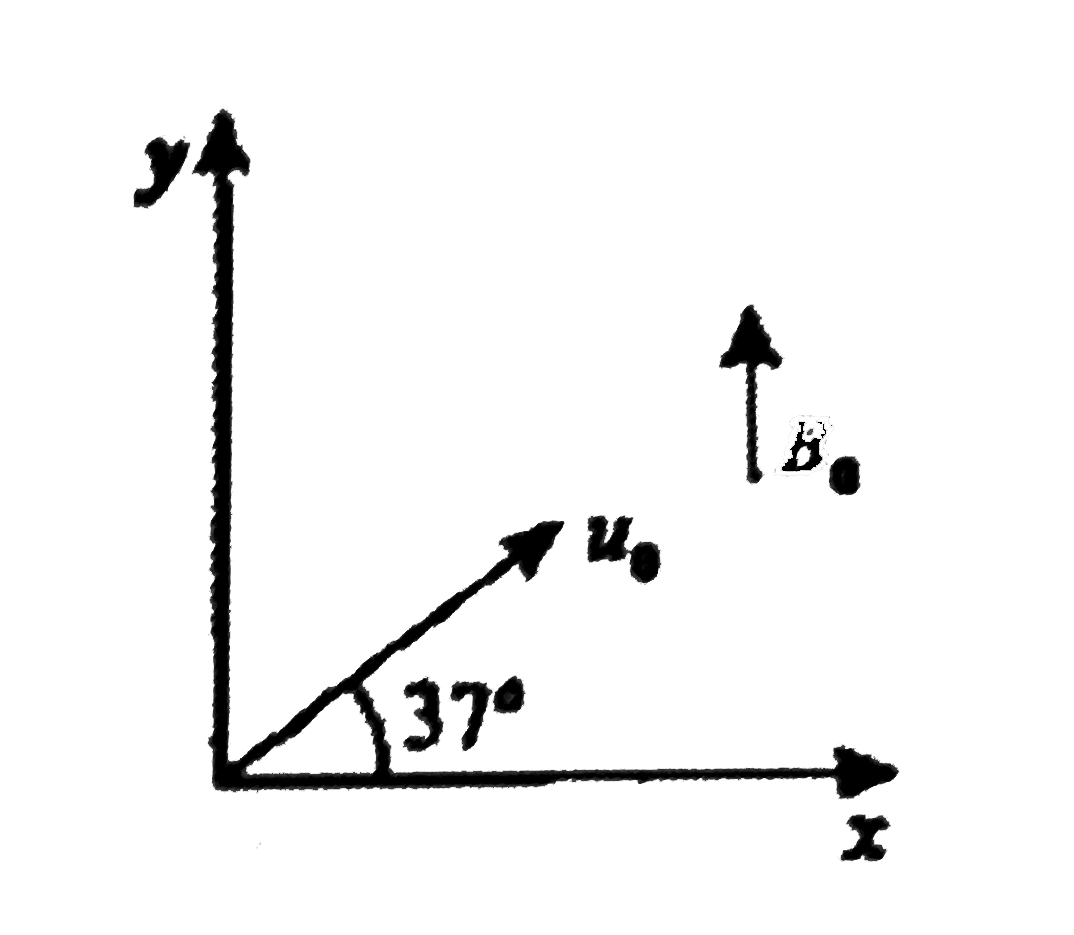
u0[√392i+35ˆj−ˆk√3]
u0[ˆi√3+ˆj√2+ˆk√6]
u0[√3910ˆi+35ˆj+14ˆk]
u0[√3910ˆi+35ˆj+12ˆk]
Step by step video & image solution for At t=0, a positively charged particle of mass m is projected from the origin with velocity u_(0) at an angle 37^(@) fromn the x-axis as sown in the figure-4.235. a constant vecB_(0)=B_(0)hatj is present in space. After a time internal t_(0) velocity of particle may be: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - Advance MCQ29videos
MAGNETIC EFFECTS OF CURRENT AND MAGNETISM
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - U.N.P79videos
MAGNETIC EFFECTS OF CURRENT AND MAGNETISM
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - Conceptual MCQ37videos
MAGNETIC EFFECTS OF CURRENT AND MAGNETISM
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO64videos
Kinetic Theory of Gases and Gas Laws
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NUCLEAR PHYSICS AND RADIOACTIVITYEXERCISE - Concptual MCQs48videos
NUCLEAR PHYSICS AND RADIOACTIVITY
Similar Questions
A particle of charge q and mass m is projected from the origin with velocity v=v0ˆi in a non uniformj magnetic fiedl B=−B0xˆk. Here v0 and B0 are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
View SolutionAt t=0, the particle is at the origin and its velocity is 10m/s at an angle 37∘ with the x-axis. The particle moves in x−y plane with a constant acceleration of 1m/s2 along the y-axis. Find the magnitude and direction of the velocity after 2s.
View Solution
Knowledge Check
- Question 1 - Select One
vx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
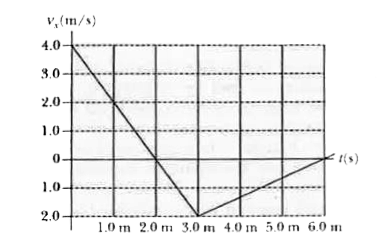 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 m - Question 2 - Select One
The electric field acts positive x-axis. A charged particle of charge q and mass m is released from origin and moves with velocity →v=v0ˆj under the action of electric field and magnetic field, →B=B0ˆi. The velocity of particle becomes 2v0 after time √3mv0√2qE0. find the electric field:
A√2√3E0ˆiB√3√2E0ˆiC(√3)E0ˆiD(√2)E0ˆi - Question 3 - Select One
A charge praticule of sepeific charge (charge/ mass ) α is realsed from origin at time t=0 with velocity v=v0(ˆi+ˆj) in unifrom magnetic fields B=B0ˆi. Co-ordinaties of the particle at time t=πB0α are
A(V02B0α,√2V0αB0,−V0B0α)B(−V0B0α,0,0)C(0,2V0B0α,V0π2B0α)D(V0π2B0α,0,−2V0B0α)
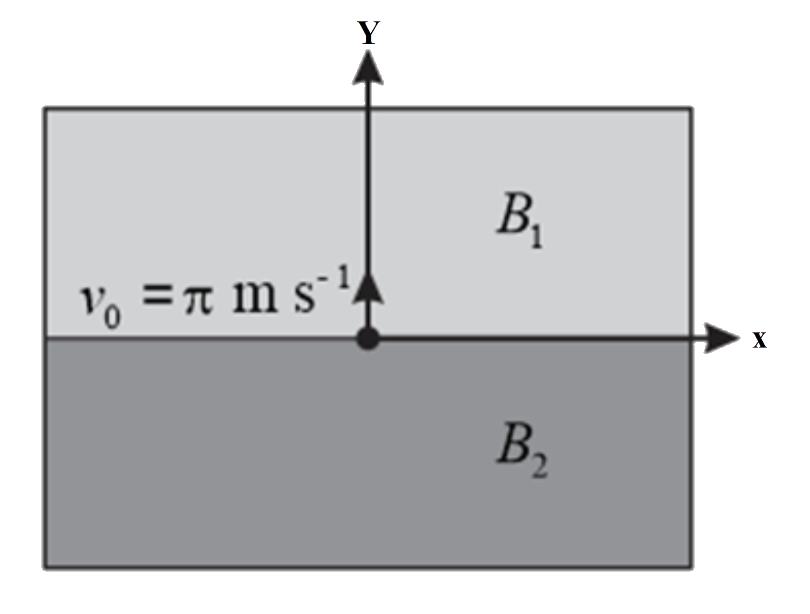
In the XY- plane , the region y>0 has a uniform magnetic field B1ˆk and the region y<0has another uniform magnetic field B2ˆk. A positively charged particle is projected from the origin along the positive y- axis with speed v0=πms−1 at t=0 , as shown in the figure . Neglect gravity in this problem . Let t=T be the time when the particle crosses the X- axis from below for the first time . If B2=4B1, the average speed to the particle , in ms−1, along the x- axis in the time interval T is __________ .
 View Solution
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.View SolutionA small particle of mass m is projected at an angle θ with x-axis with initial velocity υ0 in x-y plane as shown in Fig. Calculate the momentum of the particle
at t<υ0sinθg.
 View Solution
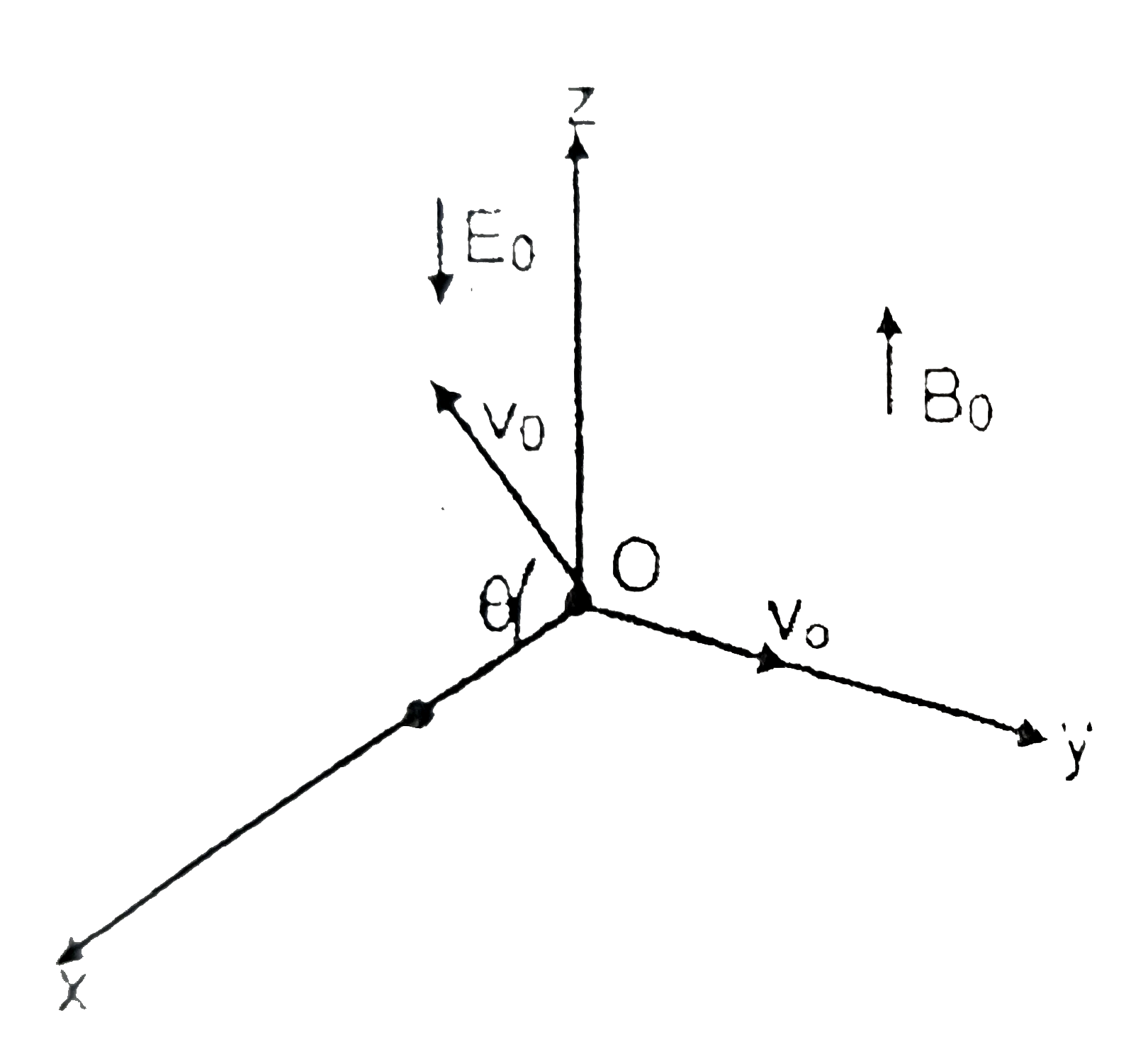
View SolutionA charged point particle having positive charge q, mass m is projected in x−z plane with a speed v0 at an angle θ with the x−axis , while another identical particle is projected simultaneously along the y−axis from the origin (see figure) with an equal speed v0.
An electric field →E=−E0ˆk exists in the x−z plane, while a magnetic field →B=B0ˆk exists in the region y>0 (F0, B0>0). It is observed that both the particles collide after some time. Assume that the space is gravity free.
(i) Find the time after which the particles collide and the coordinates of the point of collision.
(ii) Find the velocity v0 and the angle θ in terms of the other variables.
(iii) What is the maximum value of the z− coordinate of the first particle ?
 View Solution
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
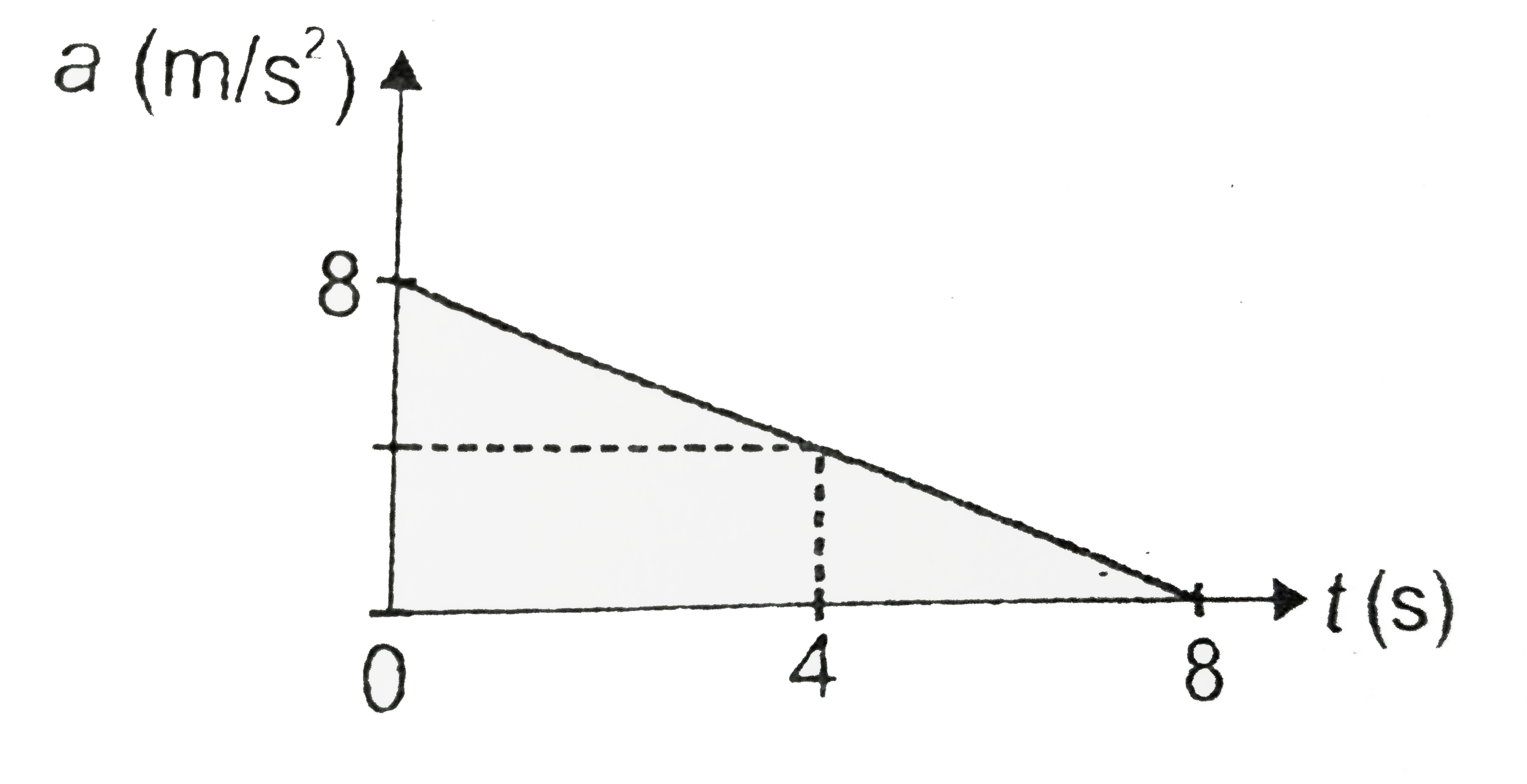 View Solution
View Solution

