A gum ball is shot at a block of wood. In which case dows the gum exert the larger impulse on the blok when it sticks or when it rebounds?
Step by step video & image solution for A gum ball is shot at a block of wood. In which case dows the gum exert the larger impulse on the blok when it sticks or when it rebounds? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Conceptual MCQ s single option correct
30 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Numerical MCQ s
75 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Practive Exercise
28 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
A bullet of mass 10 g travelling horizontally with a velocity of 300 m/s strikes a block of wood of mass 290 g which rests on a rough horizontal floor. After impact the block and the bullet move together and come to rest when the block has travelled a distance of 15 m. The coefficient of friction between the block and the floor will be - (Duration of impact is very short)
View SolutionA block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1. At the instant when the block passes through its equilibrium position a lump of putty with mass m is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.
View Solution
Knowledge Check
A bullet of mass m is fired into a block of wood of mass M which hangs on the end of pendulum and gets embedded into it. When the bullet strikes with maximum rise R. Then, the velocity of the bullet is given by
AMm+M(√2gRBM+mm√2gRC(Mm)√2gRDNone of theseConsider a case of fixed smooth sphere of radius R . A block of mass m is placed at the most poit of the sphere . A sharp impulse is applied on the block to impart it a speed v .
If a speed given at top is √gR3 , then what is the angle made by radius through block when it leaves the sphere ?Acos−1(23)Bcos−1(34)Ccos−1(59)Dcos−1(79)A block with mass (M) is connected by a massless spring with stiffness constant (k) to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position (x_0). Consider two cases : (i) when the block is at (x_0) , and (ii) when the block is at x=x0+A. In both the cases, a particle with mass m(lt M) is softly placed on the block after which they strick to each other. Which of the following statement (s) is (are) true about the motion after the mass (m) is placed on the mass (M) ?
AThe amplitude of oscillation in the first case changes by a factor of √Mm+M, whereas in the second case it remains unchanged.BThe final time period of oscillation in both the cases is same.CThe total energy decreases in both the cases.DThe instantaneous speed at (x_0) of the combined masses decreases in both the cases.
(i) A non uniform cube of side length a is kept inside a container as shown in the figure. The average density of the material of the cube is 2 ρ where ρ is the density of water. Water is gradually fille din the container. It is observed that the cube begins to topple, about its edge into the plane of the figure passing through pointA, when the height of the water in the container becomes a2. Find the distance of the centre of mass of the cube from the face AB of the cube. Assume that water seeps under the cube.
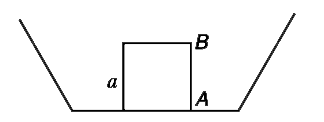
(ii) A rectangular concrete block (specific gravity =2.5) is used as a retatining wall in a reservoir of water. The height and width of the block are x and y respectively the height of water in the reservoir is z=34x. the concrete block cannot slide on the horizontal base but can rotate about an axis perpendicular to the plane of the figure and passing through point A
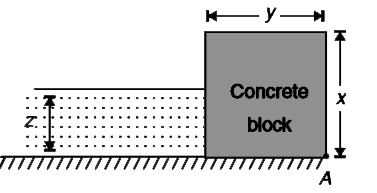
(a) Calculate the minimum value of the ratio yx for which the block will not begin to overturn about A.
(b) Redo the above problem for the case when there is a seepage and a thin film of water is present under the block. Assume that a seal at A prevents the water from flowing out underneath the block.
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Calculate the highest average speed that blood (ρ≈1000kg/m3) could have and still remain in laminar flow when it flows through the arorta (R=8×10−3m) Take the coeffiicient of viscosity of blood to be 4×10−3Pa−s
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. What is the viscous force on a glass sphere of radius r=1mm falling through water (η=1×10−3Pa−s) when the sphere has speed of 3m/s?
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. If the sphere in previous question has mass of 1×10−5kg what is its terminal velocity when falling through water? (η=1×10−3Pa−s)
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Which of the following may be concluded from the information in the passage?
View Solution
