A uniform solid cylinder of mass m and radius R is set in rotation about its axis with an angular velocity ω0, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to μ. Find
(a) how long the cylinder will move with sliding,
(b) the total work performed by the sliding friction force acting on the cylinder.
Step by step video & image solution for A uniform solid cylinder of mass m and radius R is set in rotation about its axis with an angular velocity omega_(0), then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to mu. Find (a) how long the cylinder will move with sliding, (b) the total work performed by the sliding friction force acting on the cylinder. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Discussion Question30videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Conceptual MCQs Single Option Correct39videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical63videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem81videos
NEWTONS LAWS OF MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved1videos
WORK, ENERGY AND POWER
Similar Questions
A uniform cylinder of radius R is spinned about it axis to the angular velocity ω0 and then placed into a corner,. The coeficient of friction between the corner walls and the cylinder is μk How many turns will the cylinder accomplish before it stops?
 View Solution
View SolutionA uniform cylinder of the radius R ( = 3 m) is spin about its axis at an angular velocity ω0(=40√π rad s−1) and placed between two perpendicular walls. The coefficient of friction between the walls and cylinder is μ(=2). Then, how many rotations will the cylinder make before it comes to rest?
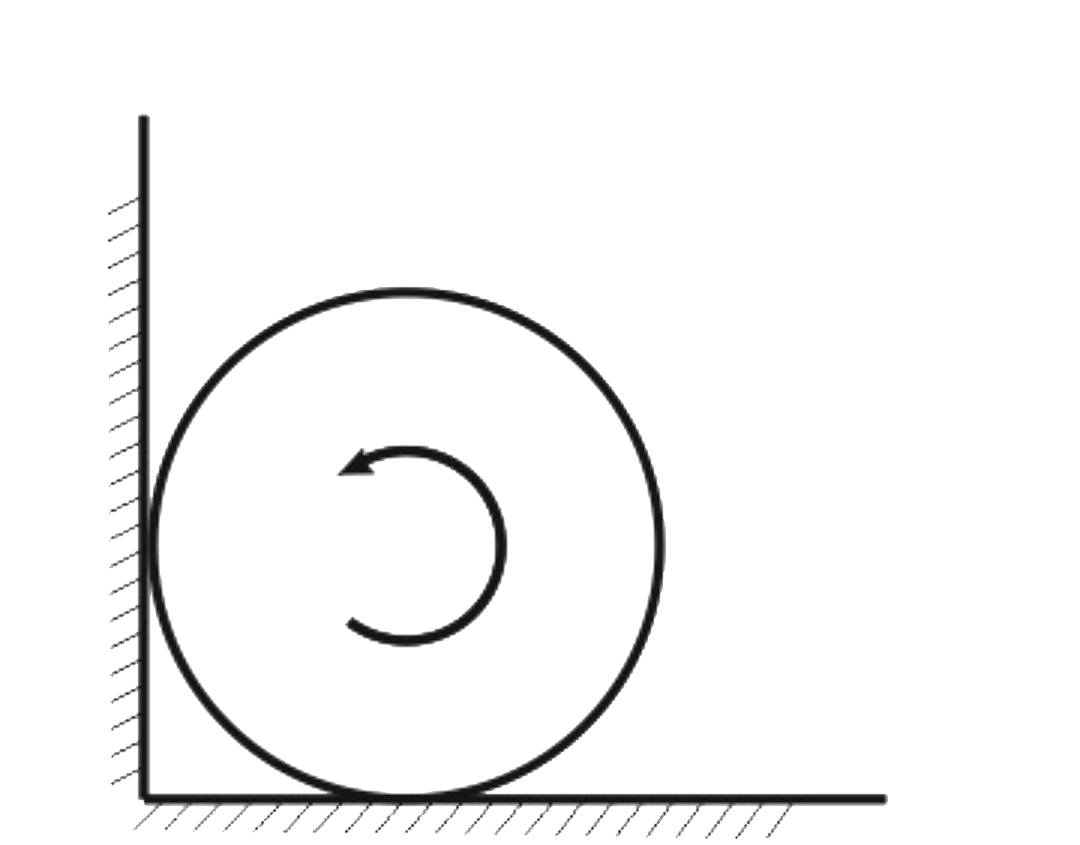 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2 - Question 2 - Select One
An cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
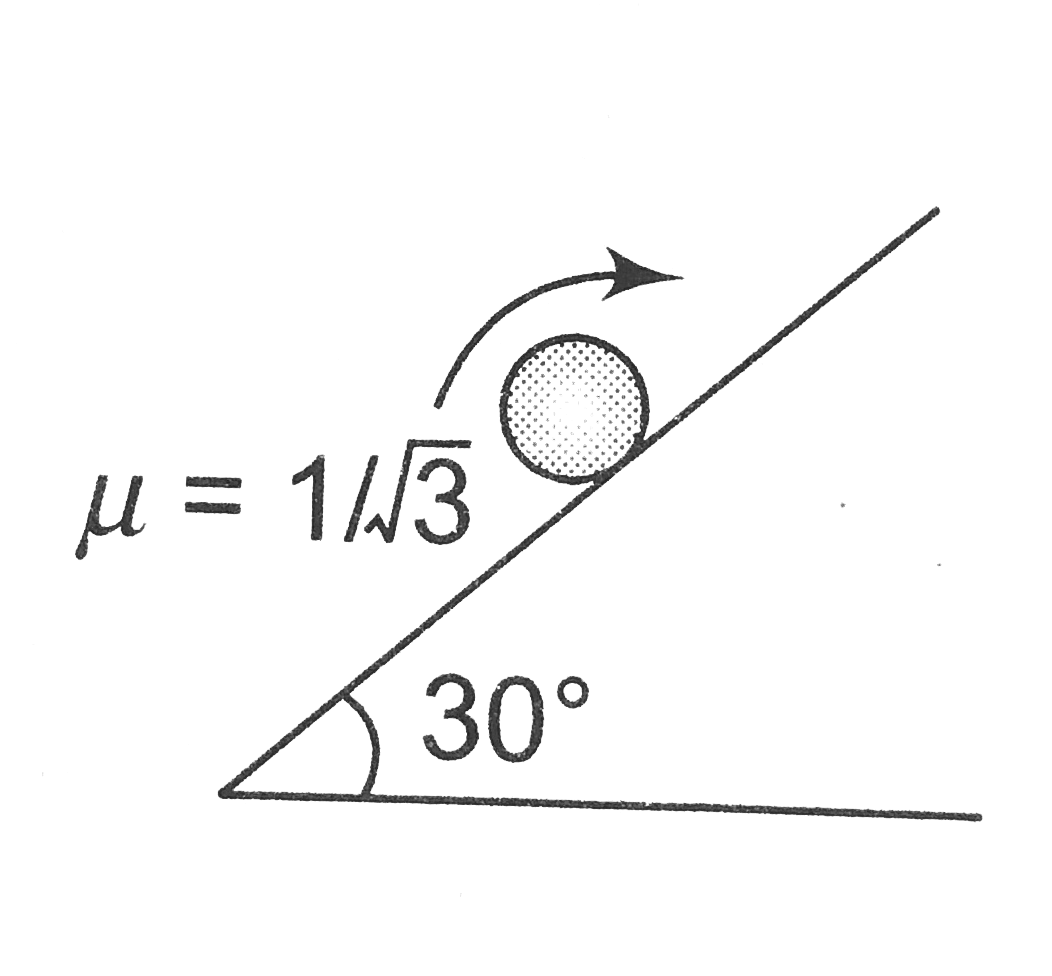 .Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward.
.Ait will start going upwardBit will first going upward and then downwardCit will go downward just after it is loweredDit can never go upward. - Question 3 - Select One
A uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is
 Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
A cylinder full of water is rotating about its own axis with uniform angular velocity ω. Then the shape of free surface of water will be
View SolutionA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
View SolutionAn solid cylinder of mass 20kg and radius 20cm rotates about its axis with a angular speed 100rads−1. The angular momentum of the cylinder about its axis is.
View Solution

