A disc of radius R is spum to an angular speed ω about its axis and then imported a horiznotal velociy of magnitude ω0R4 (at=t=0) with its plane remaining vertical. The coefficent of friction between the disc and the plane is μ The sence of rotation and direction of its lincer speed are shown. in the figure -5.97 choose the correct statement The disc will returen to its intial position :

if the value of μ<0.5
irrespective of the value of μ(μ>0)
if the value of 0.5<μ<1
if μ>1
The correct Answer is:B
Step by step video, text & image solution for A disc of radius R is spum to an angular speed omega about its axis and then imported a horiznotal velociy of magnitude (omega_(0)R)/(4) (at=t=0) with its plane remaining vertical. The coefficent of friction between the disc and the plane is mu The sence of rotation and direction of its lincer speed are shown. in the figure -5.97 choose the correct statement The disc will returen to its intial position : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Numerical MCQs Single Option Corrrect
39 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - paragraph
24 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Discussion Question
30 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
Similar Questions
A disc of radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude ω0R4 (at t=0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ. The sense of rotation and direction of its linear speed are shown in the figure. The disc returns to its initial point in time T=256kμgω0R. Find the value of k.
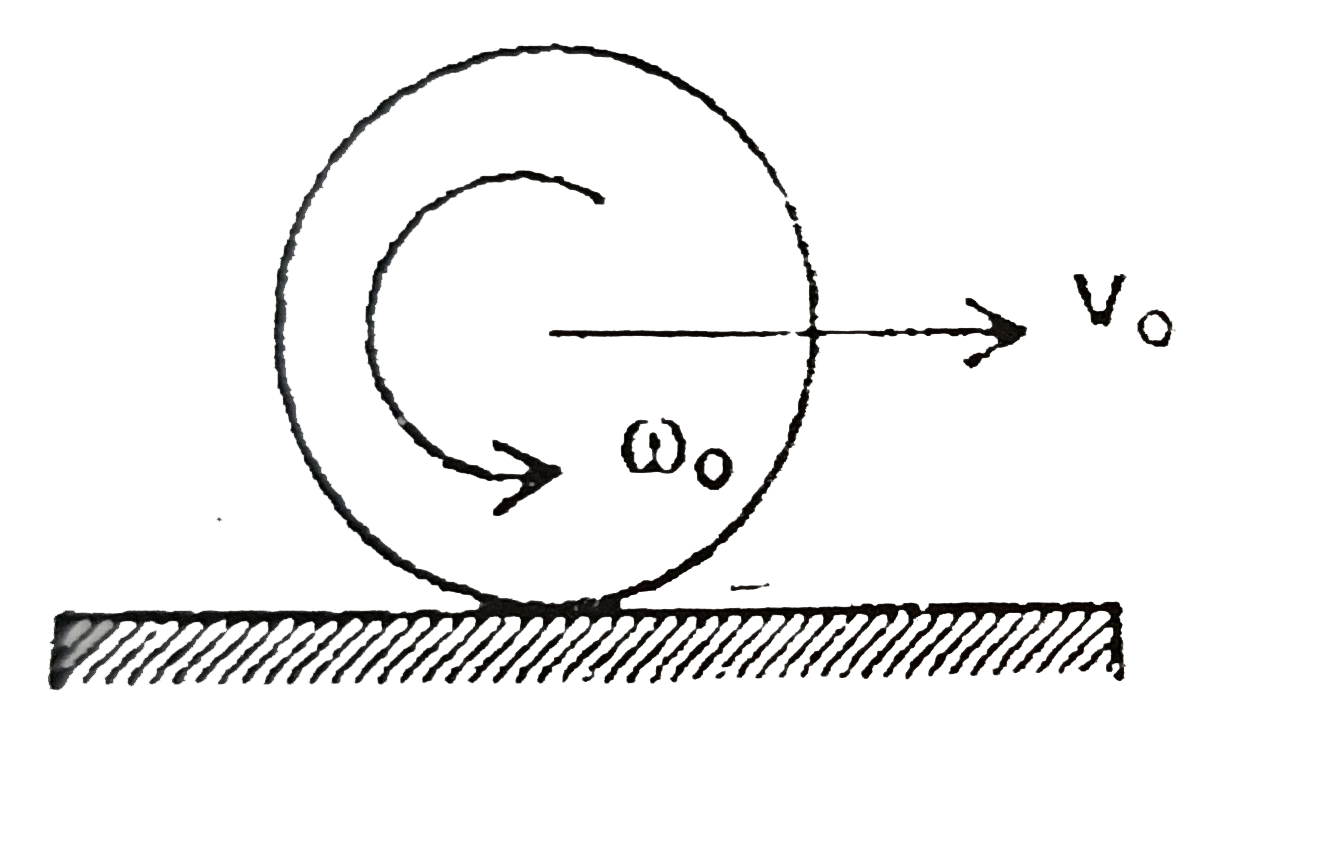
View SolutionA disc of radius R is spun to an angular speed ω0 about its axis and then imparted a horizontal velocity of magnitude ω0R4 (at t=0) with its plane remaining vertical. The coefficient of friction between the disc and the plane is μ. The sense of rotation and direction of its linear speed are shown in the figure. The disc returns to its initial point in time T=256kμgω0R. Find the value of k.
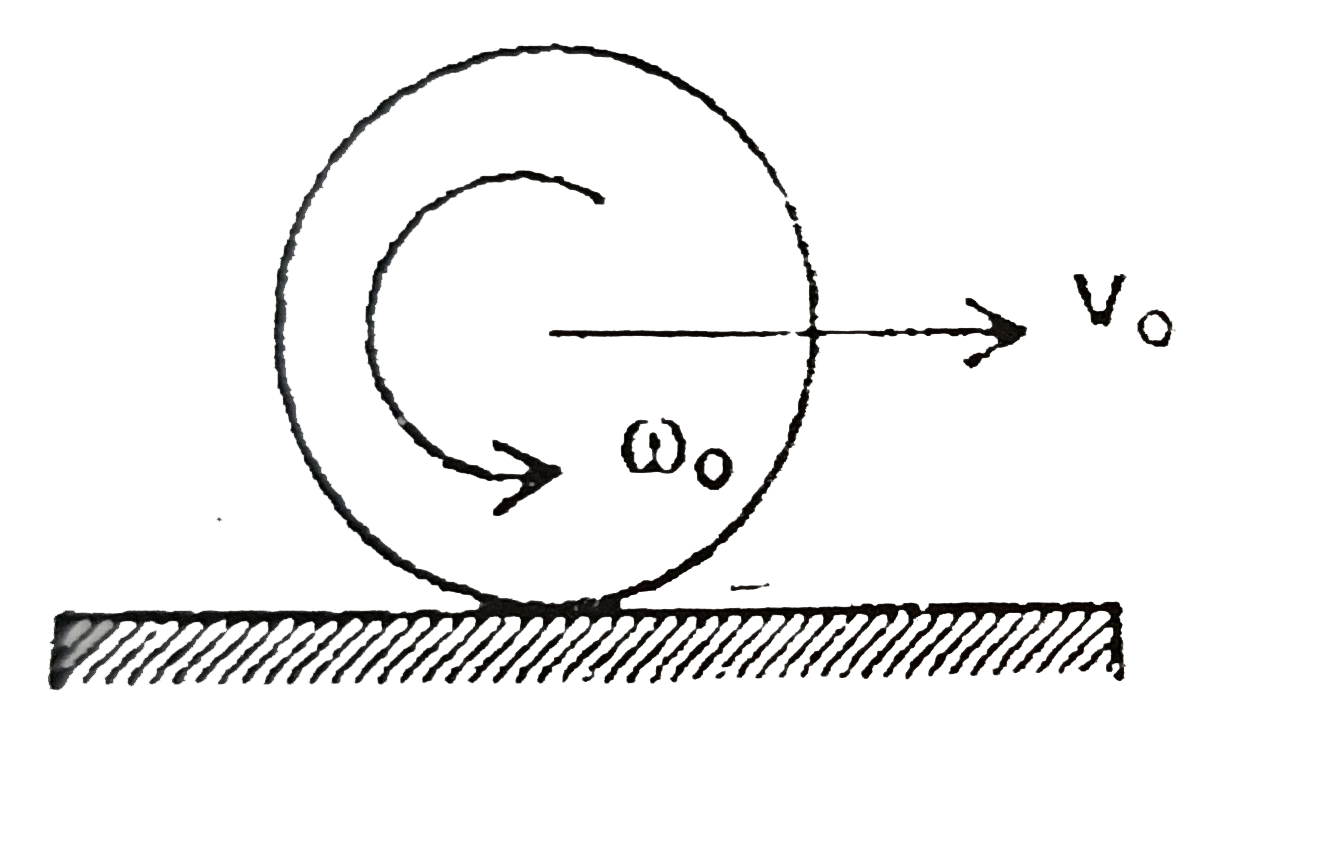
View Solution
Knowledge Check
A uniform circular ring of radius R is first rotated about its horizontal axis with an angular velocity ω0 and then carefully placed on a rough horizontal surface as shown. The coefficient of friction between the surface and the rings μ. Time after which its angular speed is reduced to 0.5ω0 is
 Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μgA disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
A(1/2)MR2ωBMR2ωC(3/2)MR2ωD2MR2ω
A disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View SolutionA metal disc of radius R rotates with an angular velcoity ω about an axis perpendicular to its plane passing through its centre in a magnetic field B acting perpendicular to the plane of the disc. Calculate the induced emf between the rim and the axis of the disc.
View SolutionA uniform disc of mass m and radius R I rotated about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficnet of friction between te disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
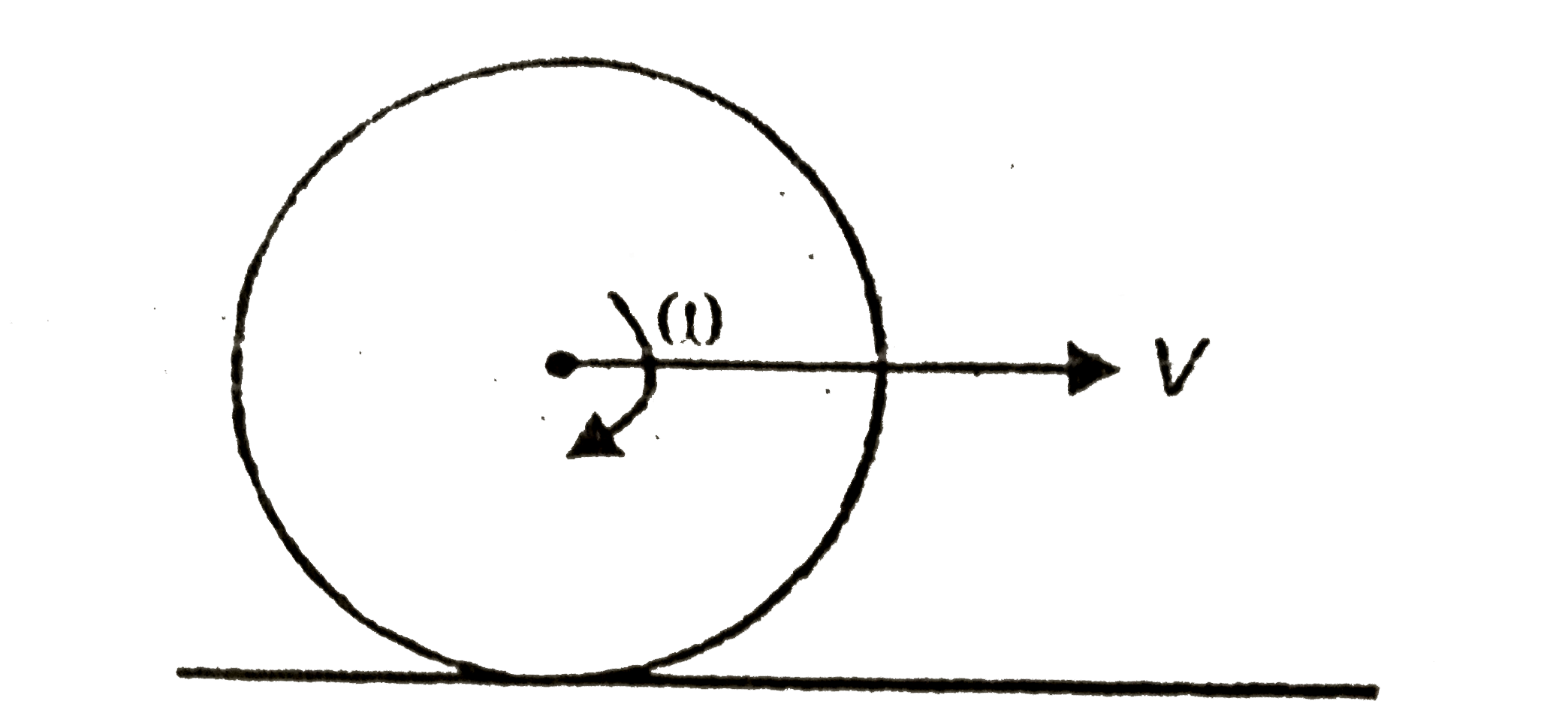
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View Solution
