A uniform rod AB of mass m=2kg and length l=1.0m is placed on a sharp support P such that a=0.4m and b=0.6m. A. spring of force constant k=600N/m is attached to end B as shown in Fig. To keep the rod horizontal, its end A is tied with a thread such that the spring is B elongated by 1CM. Calculate reaction of support P when the thread is burnt.
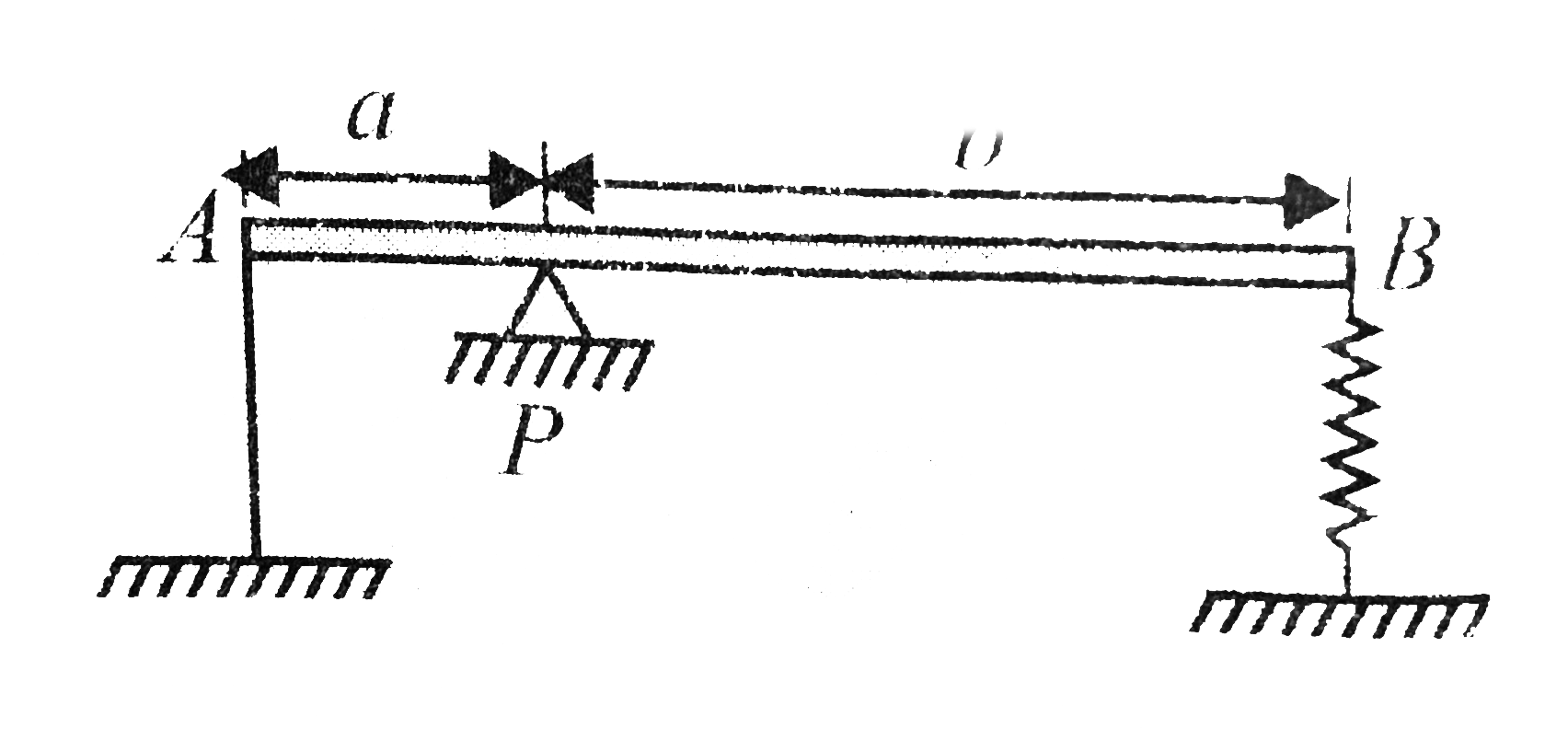
The correct Answer is:[20 N]
Step by step video, text & image solution for A uniform rod AB of mass m = 2 kg and length l = 1.0 m is placed on a sharp support P such that a = 0.4 m and b = 0.6 m. A. spring of force constant k= 600 N//m is attached to end B as shown in Fig. To keep the rod horizontal, its end A is tied with a thread such that the spring is B elongated by 1 CM. Calculate reaction of support P when the thread is burnt. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - MCQ16videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem81videos
NEWTONS LAWS OF MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved1videos
WORK, ENERGY AND POWER
Similar Questions
A uniform rod AB of mass m=2kg and length l=1.0m is placed on a sharp support P such that a=0.4m and b=0.6m. A. spring of force constant k=600N/m is attached to end B as shown in Fig. To keep the rod horizontal, its end A is tied with a thread such that the spring is B elongated by 1CM. Calculate reaction of support P when the thread is burnt.
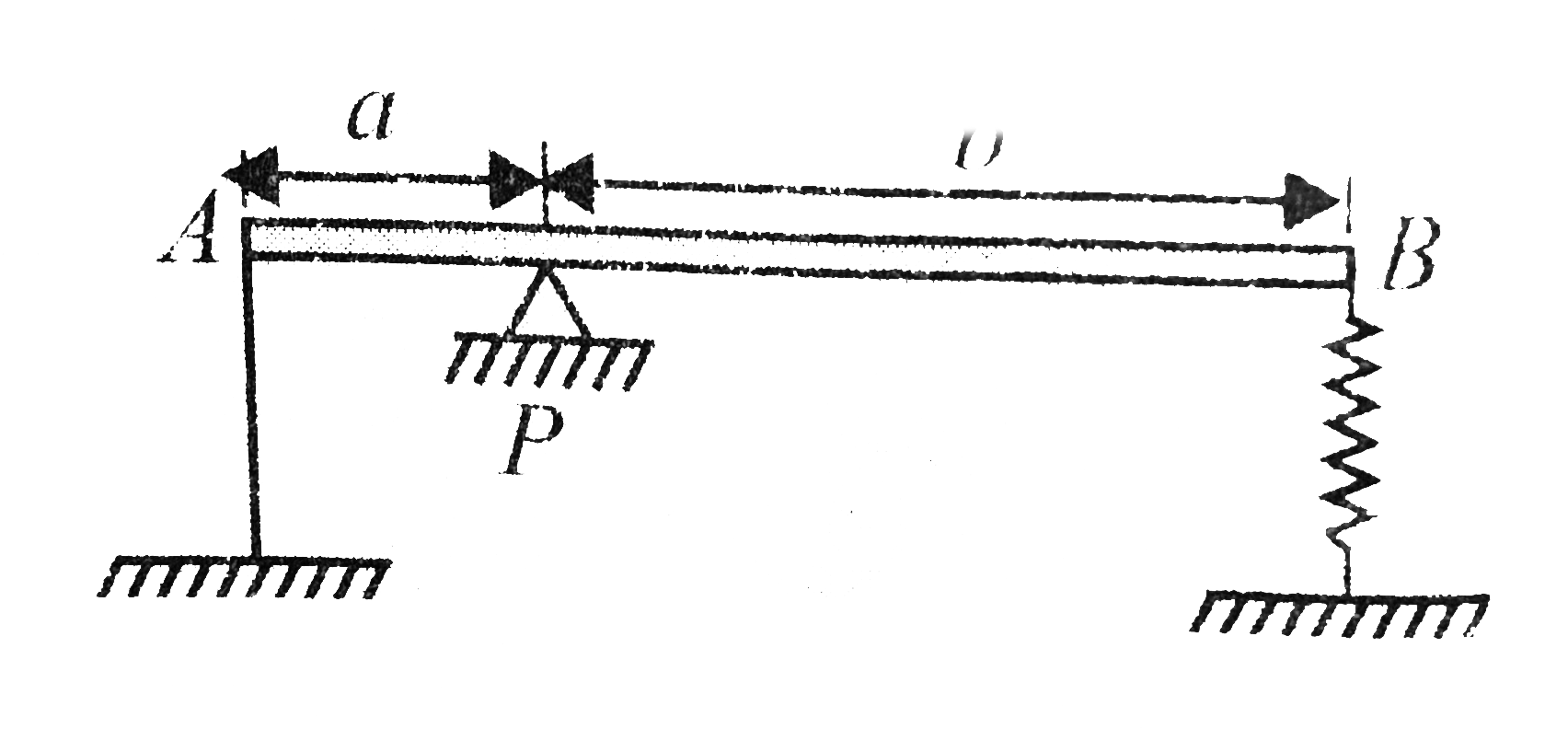 View Solution
View SolutionA uniform rod of mass 2m and length L is hinged at one end and carries a particle of mass m at the other end.Two springs each of force constant k are installed at distances as shown.The whole arrangement rests on a smooth horizontal surface.The frequency of small oscillations will be?
View Solution
Knowledge Check
- Question 1 - Select One

A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion isA√3kmB√k3mC√3km+3g2LD√km - Question 2 - Select One
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A(2πmlpB(2π)(pmlCπml12pDπpml - Question 3 - Select One
A uniform rod AB of mass m and length l at rest on a smooth horizontal surface. An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 A2πmlPBπml3PCπml12PD2πml3P
A2πmlPBπml3PCπml12PD2πml3P
A horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
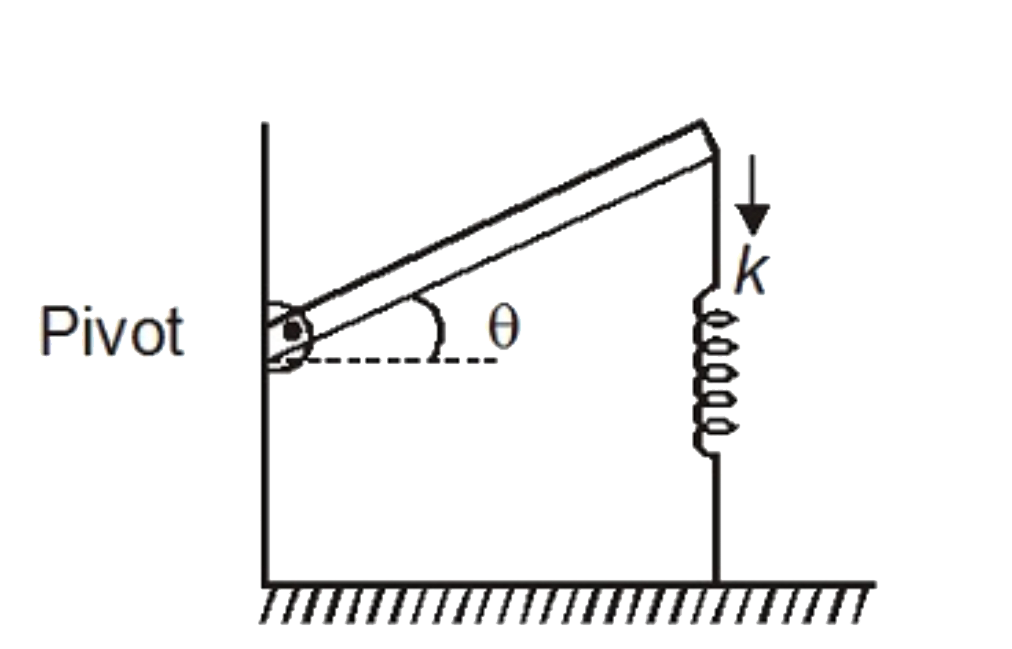 View Solution
View SolutionA unifrom rod of mass m and length L is kept on a horizontal table with L4 length on the table. The end B is tied to a string as shown in the figure. The string attached to the end B is cut and the rod starts rotating about point C. Find the normal reaction from the table on the earth as soon as the string is cut.
 View Solution
View SolutionA mass M attached to a spring of spring constant 0.7 N/m oscillates on a smooth horizontal table. When displacement is 0.3 m, velocity is 2 ms−1. And when displacement is 0.4 m, velocity is 0.3 m/s. Calculate the vlaue of M.
View SolutionA long uniform rod of length L, mass M is free to rotate in a horizontal plane about a vertical axis through its end. Two springs of constant K each are connected as shown. On equilibrium, the rod was horizontal. The frequency will be –
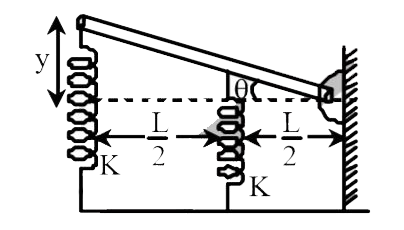 View Solution
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 View Solution
View Solution

