Assume that the runner in sample question completes the race in 1 hour and 20 seconds. Find her average speed and the magnitude of her average velocity.
Average speed is total distance divided by leaped time Since the length of the track is 500 m, the runner's average speed was . However, since her displacement was zero, her average velocity was zero also : .
Topper's Solved these Questions
Similar Questions
Assume that the runner in sample question completes the race in 1 hour and 20 seconds. Find her average speed and the magnitude of her average velocity.
View SolutionAverage speed cannot be ______ than magnitude of average velocity.
View SolutionIn which condition the magnitude of average speed is equal to the magnitude of average velocity?
View SolutionFor a moving object is it possible that magnitude of average speed is less than magnitude of average velocity ?
View SolutionAre the magnitudes of average velocity and average speed equal?
View SolutionA girl is jogging along a circular path of radius. 25. 0 m. In 1 110.0 second she jogs a. quarter ofa circle starting from point1 P. (a) Compute her displacement and average velocity, and (b) Compute the magnirude of the runner's average velocity and her average speed.
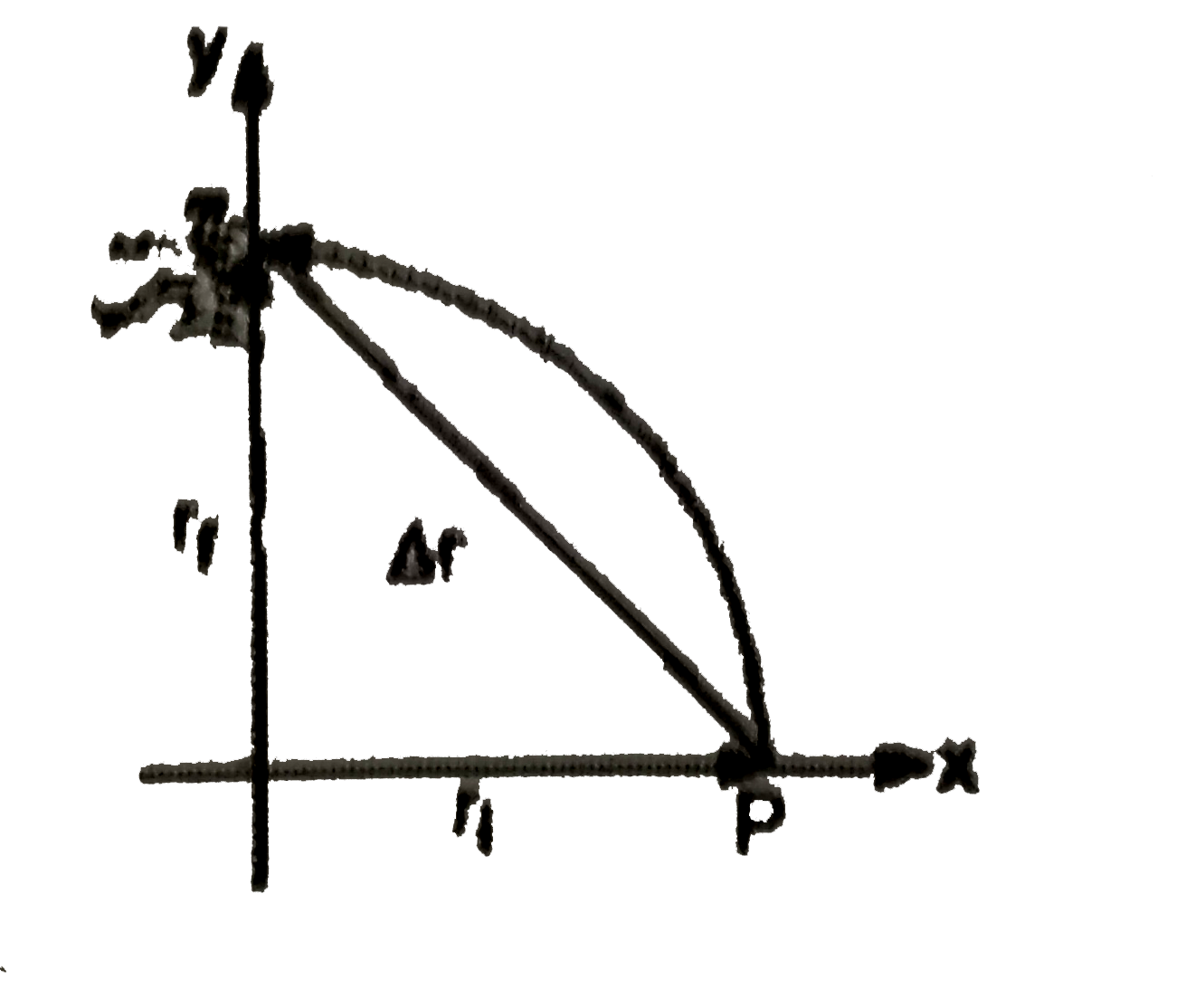
View SolutionA clock has its second hand 2.0cm long. Find the average speed and modulus of average velocity of the tip of the second hand in 15s.
View SolutionA clock has its second hand 2.0cm long. Find the average speed and modulus of average velocity of the tip of the second hand in 15s.
View SolutionDeepa rides her bike at an average speed of 30 km/hr and reaches her destination in6 hours. Hema covers the same distance in 4 hours. If Deepa increases her average speed by 10 km/hr and Hema increases her average speed by 5 km/hr what would be the difference in their time taken to reach the destination? 40 m∈utes b. 45 m∈utes c. 4 m∈utes d. 1 hour e. none of these
View SolutionExplain with example the distinction between the magnitude of average velocity and average speed over the same period. Show that and the average speed is either greater than or equal to the average velocity. When is the equality sign true?
View Solution
