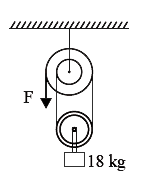
In the figure below, how much force would we need to exert on the free end of the cord in order to lift the plank (mass m= 300 kg) with constant velocity ?

Text Solution

Verified by Experts

There are a total of six tension forces pulling upward on the plank. In order to lift with a constant velocity our net force should be zero since there is no acceleration. The total of all tension forces pulling up, $6 F_{T}$ , must balance out with the weight of the plank, mg. This gives us :
$6 F_{T} = m g$
$F_{T} = \frac{m g}{6} = \frac{(300 k g) (10 N / k g)}{6} = 500 N$

Updated on:21/07/2023

In the figure at the free end a force F is applied to keep the suspended mass of 18 kg at rest. The value of F is-

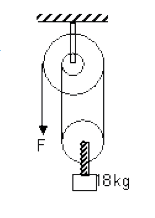A180 N
B90 N
C60 N
D30 N
A lift of mass 920 kg has a capacity of 10 persons. If average mass of person is 68 kg. Friction force between lift and lift shaft is 6000 N. The minimum power of motor required to move the lift upward with constant velocity 3 m/s is [ $g = 10 \frac{m}{s^{2}}$ ]
A66000W
B63248W
C $48000 W$
D $56320$
A chain of length L and mass per unit length $ρ$ is piled on a horizontal surface. One end of the chain is lifted vertically with constant velocity by a force P.
AP as function of height x of the end above the surface will be $ρ (g x + v^{2})$
Bno energy will loss in this process.
Cwork done by force will be $\frac{1}{2} ρ g L^{2} + ρ v^{2} L$
Dloss in energy $\frac{1}{2} ρ g L v^{2}$