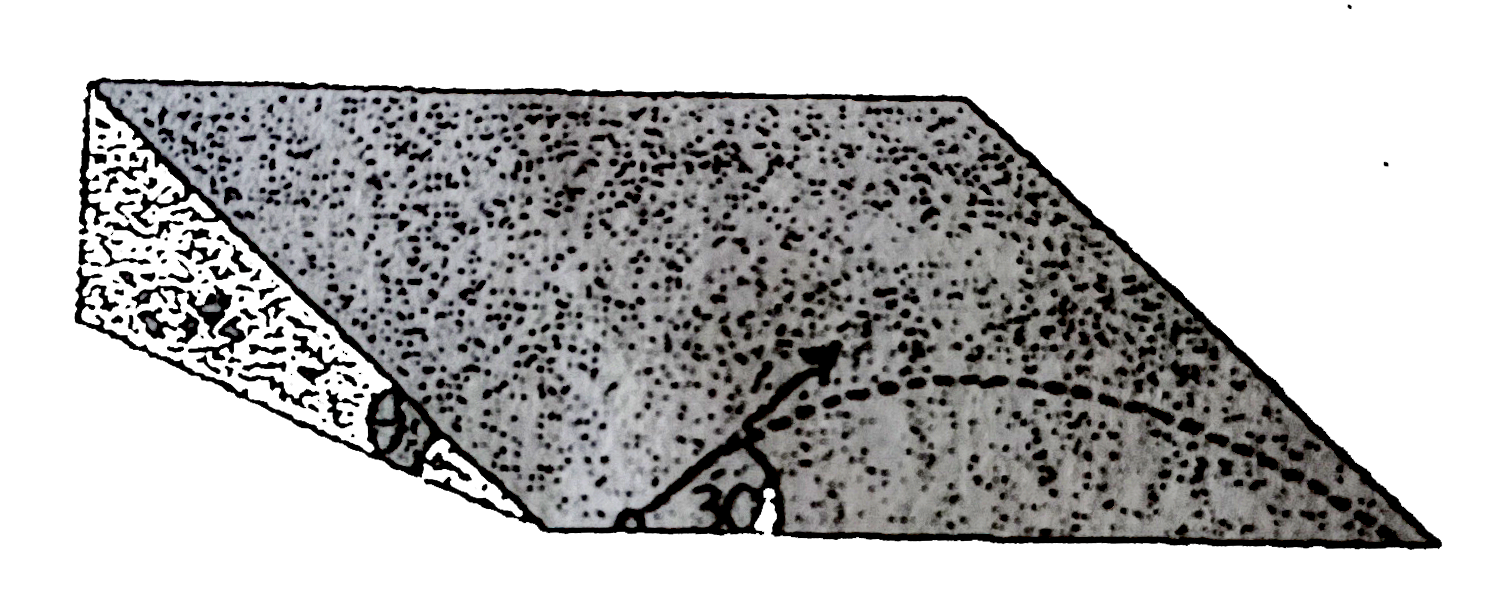
A box is projected up a long ramp (incline angle with the horizontal=30∘) with an initial speed of 8m/s. if the surface of the ramp is very smooth (essentially frictionless), how high up the ramp will the box go? What distance along the ramp will it slide?
Because friction is negligible, we can apply conservation of mechanical energy. Calling the bottom of the ramp our h=0 reference level, we write
Ki+Ui=Kf+Uf
12mv02+0=0+mgh
h=12v20g ltBrgt =12(8m/s)210m/s2
=3.2m
Since the incline angle is θ=30∘, the distance, d, it slides up the ramp is found in the following way.

h=dsinθ
d=hsinθ=3.2msin30∘=6.4m.
Topper's Solved these Questions
Similar Questions
A small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘to the bottom edge of the slope .It returns to the edge after 2s . The ball is in contact with the inclied plane throughout the process. The angle of inclination θ is :−.
View SolutionA box of 5 kg mass moves up a ramp from point A to point B at a constant speed. Given that the surfaces are smooth (frictionless). What is the gain in the potential energy by the box? (Take g = 10 m/s2)
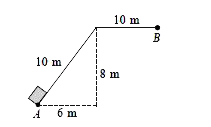
View Solution
Knowledge Check
A small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘ to the bottom edge of the slope. It returns to the edge after 2s. The ball is in constant with the inclined plane throughout the process. What is the inclination angle of the plane?
 A15∘B60∘C37∘D30∘
A15∘B60∘C37∘D30∘A small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘to the bottom edge of the slope .It returns to the edge after 2s . The ball is in contact with the inclied plane throughout the process. The angle of inclination θ is :−.
 A45∘B53∘C30∘D37∘
A45∘B53∘C30∘D37∘
Danielle is a civil enginner for Dastis Dynamic Construction, Inc. She must create blueprints for a wheelchair accessible ramp leading up to the entrance of a mall that she and her group are building. The ramp must be exactly 100 meters in length and make a 20∘ angle with the level ground. What is the horizontal distance, in meters, from the start of the ramp to the point level with the start of the ramp immediately below the entrance of the mall, rounded to the nearest meter? (Disregard units when inputting your answer)
View SolutionA rectangular box lies on a rough inclined surface. The coefficient of friction between the surface and the box is (μ) Let the mass of the box be m.
At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
View SolutionA block slides down an inclined plane of angle 53∘ with constant velocity .It is then projected up the same plane with an initial velocity of 8m/s . How far up (in m) the inclione will it move before coming to rest?
View SolutionA crate, in the form of a cube with edge lengths of 1.2 m, contains a piece of machinery, the center of mass of the crate and its contents is located 0.30 m above the crate's geometrical center. The crate rests on a ramp that makes an angle θ with the horizontal. As θ is increased from zero, an angle will be reached at which the crate will either tip over or start to slide down the ramp. If the coefficient of static friction between ramp and crate is 0.30, (a) does the crate tip or slide and (b) at what angle θ does this occur? If μs=0.70, (c) does the crate tip or slide and (d) at what angle θ does this occur? (Hint: At the onset of tipping, where is the normal force located?)
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .

View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View Solution
