Three thin, uniform rods each of length L are arranged in the shape of an inverted U.

The rods on the arms of the U each have mass m, the third rod has mass 2m. How far below the midpoint of the horizontal rod is the center of mass of this assembly?
L8
L4
3L8
L2
The correct Answer is:B
First, replace each rod by concentrating its mass at its center of mass position.
 ltBrgt The center of mass of the two m's is at their midpoint, at a distance of 12L below the center of mass of the rod of mass 2m.
ltBrgt The center of mass of the two m's is at their midpoint, at a distance of 12L below the center of mass of the rod of mass 2m.

Now, applying the equation for locating the center of mass (letting y=0 denote the position of the center of mass of the top horizontal rod), we find
ycm=(2cm)(0)+(2m)(12L)2m+2m=14L
Topper's Solved these Questions
Similar Questions
Three uniform thin rods, each of length L=24 cm, form an inverted U. The vertical rods each have a mass of 14 g, the horizontal rod has a mass of 42 g. What are (a) the x coordinate and (b) the y coordinate of the system's center of mass?
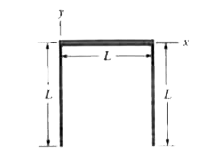
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View Solution
Knowledge Check
Three thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
AML23B2ML23C2ML26DML2Three thin uniform rods each of mass M and length L and placed along the three axis of a Cartesian coordinate system with one end of each rod at the origin. The M.I. of the system about z-axis is
AML23B2ML23CML26DML2A thin rod of length L is bent to form a semi circle. The mass of the rod is M. What will be the gravitational potential at the centre of the circle?
A−GMLB−GM2πLC−πGM2LD−πGML
Two uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionTwo identical uniform rods AB and CD, each of length L are jointed to form a T-shaped frame as shown in figure. Locate the centre of mass of the frame. The centre of mass of a uniform rod is at the middle point of the rod.

View SolutionShow that the centre of mass of uniform rod of mass M and length L lies at the middle point of the rod.
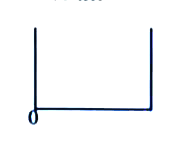
View SolutionThree identical rods each of length L and mass m are joined to form a U -shape as shown in figure. The distance of centre of mass of combined system from the corner .O. is
View SolutionA uniform rod of mass M and length L lies on a frictionless horizontal plane. A particle of same mass M moving with speed v0 perpendicular to the length of the rod strikes the end of the rod and sticks to it. Find the velocity of the center of mass and the angular velocity about the center of mass of (rod + particle) system.
View Solution
