A constant voltage is applied to n groups of resistors in siries where each group has m identical resistros in parallel. One resistor burns out in one group. Find the percentage increase of current in each resistor of the faulty group, and the percentage decrease of current in each resistor of the second group.
The correct Answer is:(n−1)100nm−n+1, (100)/(nm-n+1)
Topper's Solved these Questions
- FUNDAMENTAL OF CURRENT ELECTRICITYBOOK - NN GHOSHCHAPTER - FUNDAMENTAL OF CURRENT ELECTRICITYEXERCISE - Exercises
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NN GHOSHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERICISES-B
18 Videos
- GALVANOMETERS: AMMETER AND VOLTMETERSBOOK - NN GHOSHCHAPTER - GALVANOMETERS: AMMETER AND VOLTMETERSEXERCISE - Exercise
32 Videos
Similar Questions
Knowledge Check
In the given circuit the resistance of all the resistors is equal to 2Ω, find the current flowing through each resistor under steady state. Select the correct options.
 Acurrent through R1→5ABcurrenth through R2→5ACcurrent through R3→ zeroDcurrent through R4→5A
Acurrent through R1→5ABcurrenth through R2→5ACcurrent through R3→ zeroDcurrent through R4→5A
Current through R5→5A
Current through R6→10A
Find the current in each resistor in the circuit as shown in fig.

View SolutionTwo resistors of resistance 10Ω and 20Ω are connected in parallel. A battery supplies 6 A of current to the combination. Calculate the current in each resistor.
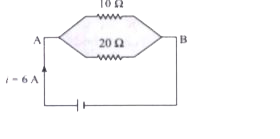
View SolutionFind current passing through the battery and each resistor.

View SolutionFind current passing through the battery and each resistor.

View SolutionA cell supplies a current of 1.2 A through two resistors each of 2 Ω connected in parallel. When the resistors are connected in series, it supplies a current of 0.4 A. Calculate :
e.m.f. of the cell.
View SolutionTwo resistors of 4Ωand6Ω are connected in parallel to a cell to draw 0.5 A current from the cell.
Calculate the current in each resistor.
View SolutionThree resistors having resistances of 1.60Ω,2.40Ω and 4.80Ω are connected in parallel to a 28.0V battery that has negligible internal resistance. Find
(a) the equivalent resistance of the combination.
(b) the current in each resistor.
(c) the total current through the battery.
(d) the voltage across each resistor.
(e) the power dissipated in each resistor.
(f) which resistor dissipates the maximum power the one with the greatest resistance or the least resistance? Explain why this should be.
View Solution

