Two long straight conductors are connected radially to two arbitary points A and B of a circular conductor. Calculate the magnetic field at the center of the coil.
The correct Answer is:Zero
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENTBOOK - NN GHOSHCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Exercises
25 Videos
- MAGNETIC DIPOLEBOOK - NN GHOSHCHAPTER - MAGNETIC DIPOLEEXERCISE - EXERCISES
10 Videos
- MAGNETIC FIELD AND POTENTIALBOOK - NN GHOSHCHAPTER - MAGNETIC FIELD AND POTENTIALEXERCISE - EXERCISES B
1 Videos
Similar Questions
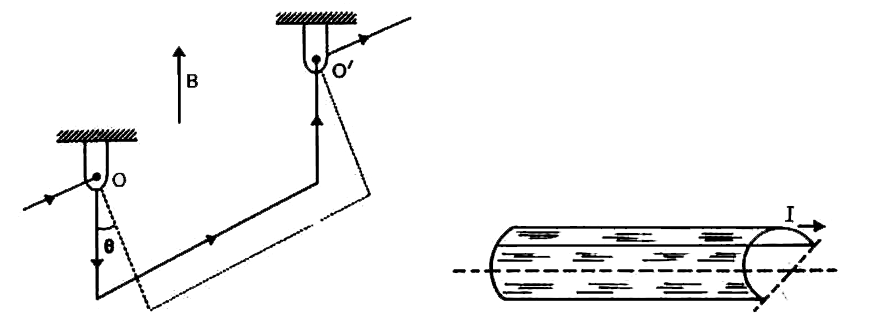
A cell is connected across two points P and Q of a uniform circular conductor, figure. Prove that the magnetic field at its centre O will be zero.
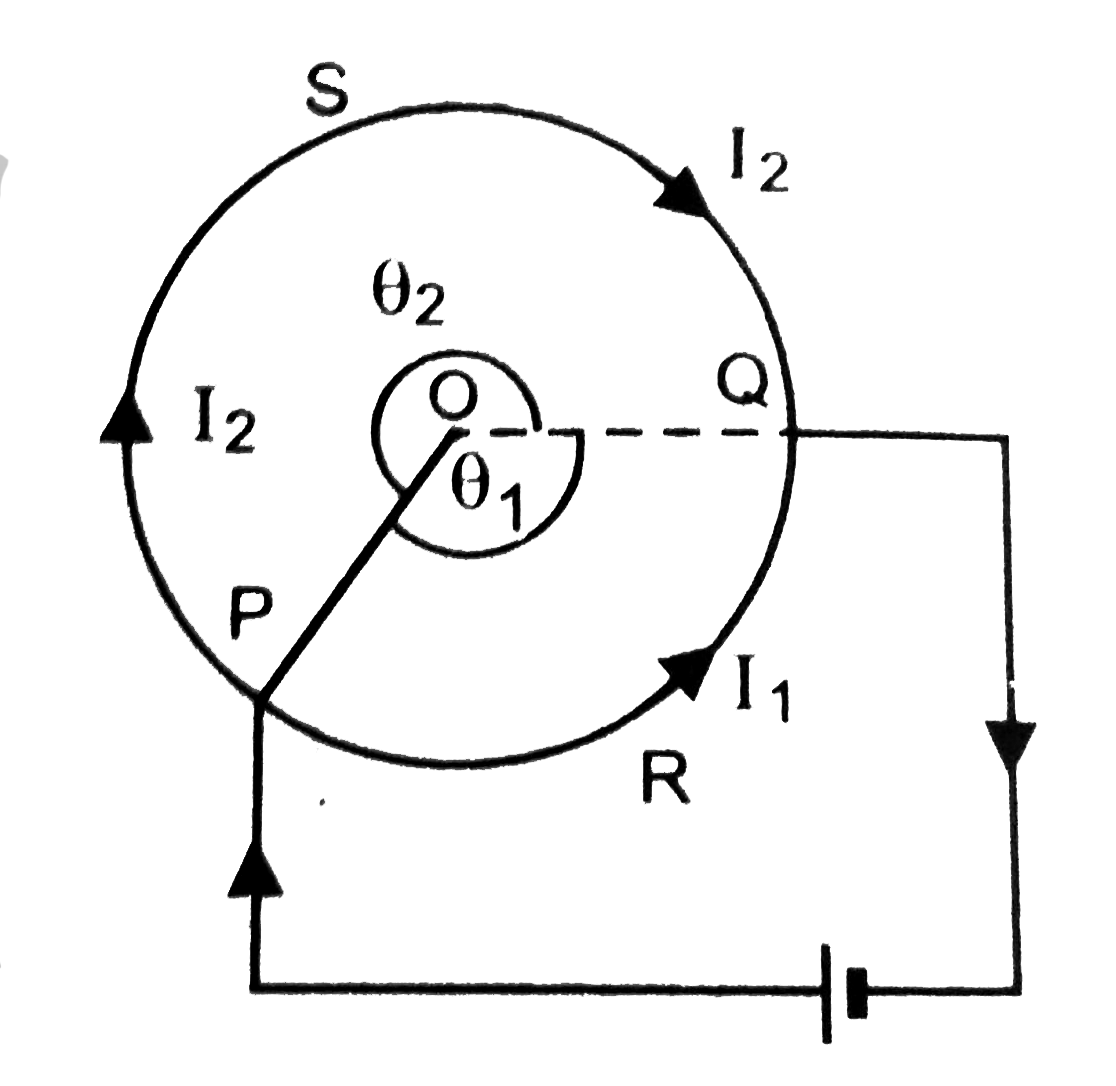
View SolutionAs shown in figure a cell is connected across two points A and B of a uniform circular conductor of radius r. Prove that the magnetic field induction at its centre O will be zero.
View Solution
Knowledge Check
A long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop
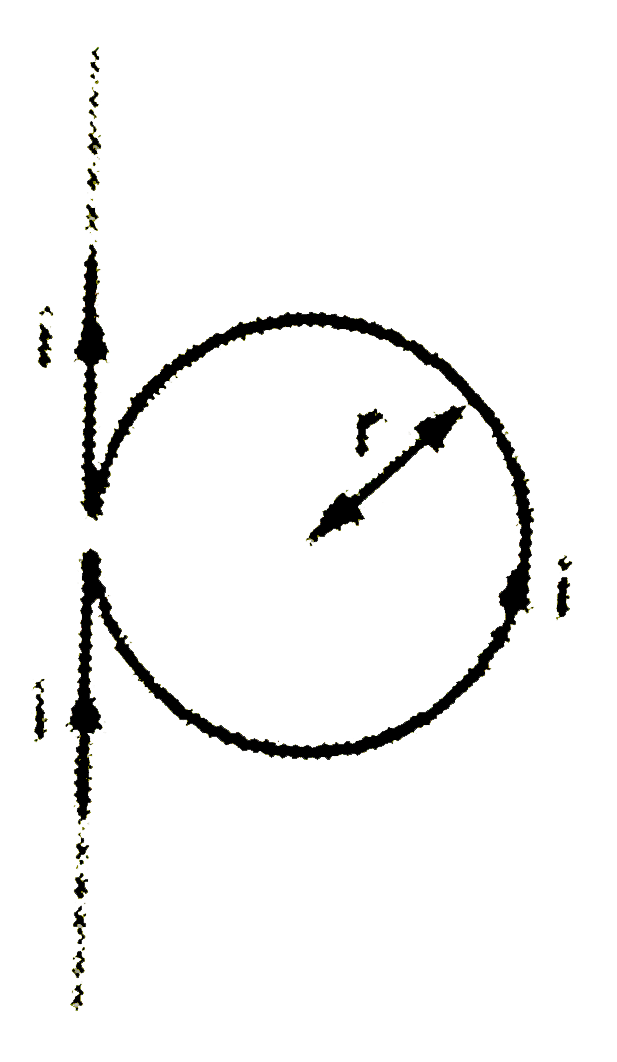 Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)
Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)A cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
AzeroBμ04π(I1−I2)Cμ02a(I1+I2)Dμ0a(I1+I2)On connecting a battery to the two corners of a diagonal of a square conductor frame of side a the magnitude of the magnetic field at the centre will be
AZeroBμ0πaC2μ0πaD4μ0iπa
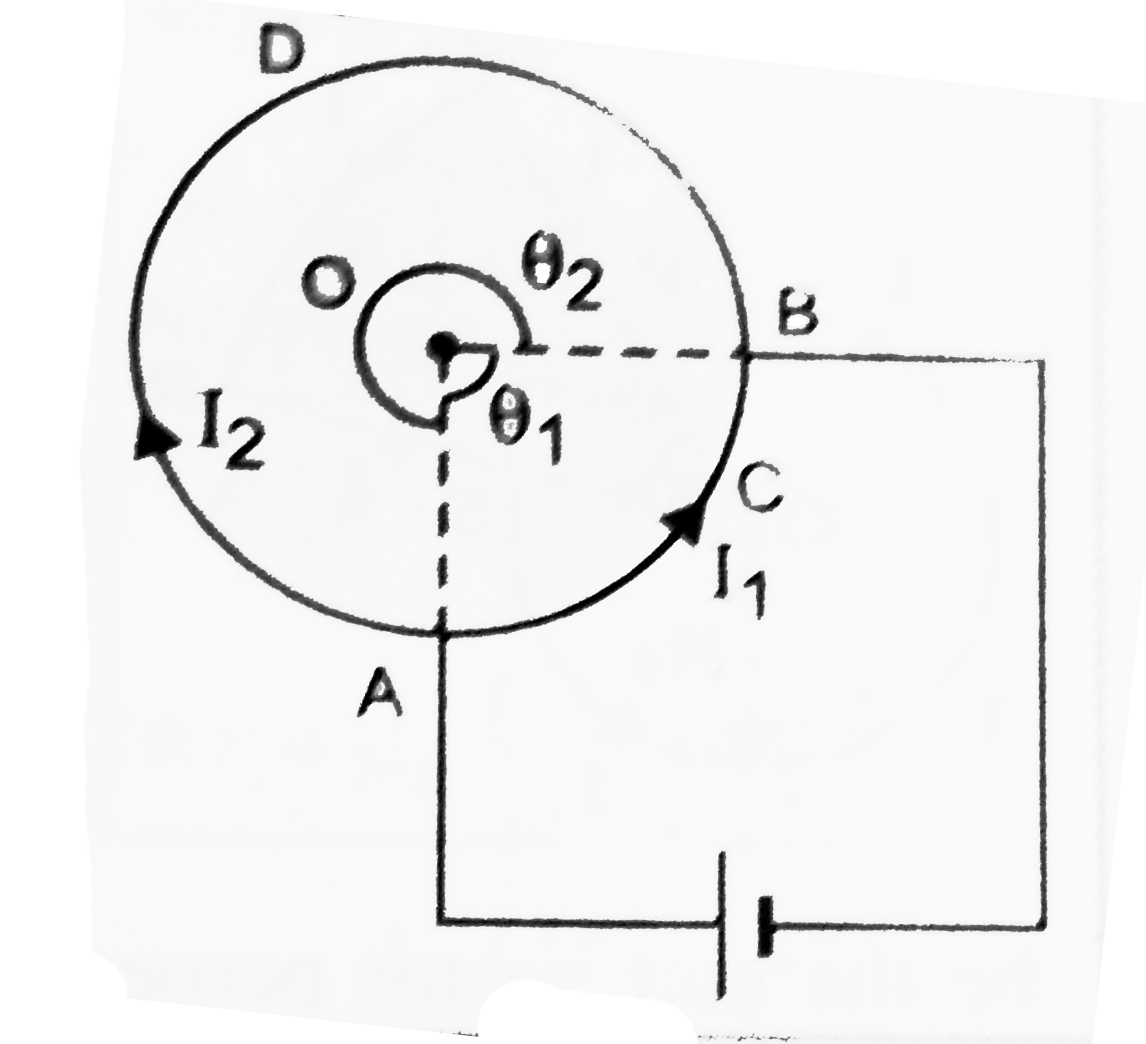
As shown in figure a cell is connected across two points A and B of a uniform circular conductor of radius r. Prove that the magnetic field induction at its centre O will be zero.

View SolutionAn infinitely long straight conductor is bent into the shape as shown in figure. It carries the current I and radius of the circular loop is a, then the magnetic field at the centre of the loop is ______
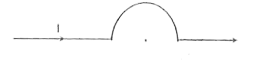
View SolutionIn figure bcdf is a circular coil of non-insulated thin uniform conductors, ab and de are very long straight parallel conductors, ab and de are very long straight parallel conductors, tangential to the coil at the points b and d. If the current 5A enters the coil from a to b, find the magnetic field induction at O, the centre of the coil. The diameter of the coil is 10cm.

View SolutionOn connecting a battery to the two corners of a diagonal of a square conductor frame of side a the magnitude of the magnetic field at the centre will be
View SolutionA conductor of length L and carrying current i is bent to form a coil of two turns.Magnetic field at the centre of the coil will be
View Solution
